上一个答案的回顾
在之前的答案中,我没有提到两种方法之间的区别。通常情况下,如果我们选择最大似然推断,我建议使用MASS::fitdistr,因为对于许多基本分布,它执行精确推断而不是数值优化。 ?fitdistr文档已经很清楚了:
对于正态,对数正态,几何,指数和泊松分布,使用闭合形式的MLE(和精确标准误差),不应提供“start”。
对于所有其他分布,使用直接优化对数似然来计算观察到的信息矩阵的估计标准误差,通过数值近似计算。 对于一维问题,使用Nelder-Mead方法,对于多维问题,使用BFGS方法,除非提供了名为“lower”或“upper”的参数(在使用“L-BFGS-B”时)或显式提供了“method”。
另一方面,fitdistrplus::fitdist始终以数字方式进行推断,即使存在精确推断也是如此。 当然,fitdist的优点在于更多的推断原则可用:
通过最大似然(mle),矩匹配(mme),分位数匹配(qme)或最大化拟合度评估(mge)将单变量分布适合非截断数据。
此答案的目的
本答案将探讨正态分布的精确推断。它将具有理论味道,但没有似然原则的证明;仅给出结果。基于这些结果,我们编写自己的R函数进行精确推断,可以与MASS::fitdistr进行比较。另一方面,为了与fitdistrplus :: fitdist进行比较,我们使用optim以数字方式最小化负对数似然函数。
这是一个学习统计和相对高级使用optim的绝佳机会。为方便起见,我将估计尺度参数:方差,而不是标准误差。
正态分布的精确推断


自己编写推断函数
以下代码已经很好地注释了。有一个开关exact。如果设置为FALSE,则选择数字解决方案。
fitnormal <- function (x, exact = TRUE) {
if (exact) {
n <- length(x)
mu <- sum(x) / n
phi <- crossprod(x - mu)[1L] / n
invI <- matrix(c(phi, 0, 0, phi * phi), 2L,
dimnames = list(c("mu", "sigma2"), c("mu", "sigma2")))
loglik <- -(n / 2) * (log(2 * pi * phi) + 1)
return(list(theta = c(mu = mu, sigma2 = phi), vcov = invI, loglik = loglik, n = n))
}
else {
nllik <- function (theta, x) {
(length(x) / 2) * log(2 * pi * theta[2]) + crossprod(x - theta[1])[1] / (2 * theta[2])
}
gradient <- function (theta, x) {
pl2pmu <- -sum(x - theta[1]) / theta[2]
pl2pphi <- -crossprod(x - theta[1])[1] / (2 * theta[2] ^ 2) + length(x) / (2 * theta[2])
c(pl2pmu, pl2pphi)
}
init <- c(sample(x, 1), sample(abs(x) + 0.1, 1))
z <- optim(par = init, fn = nllik, gr = gradient, x = x, lower = c(-Inf, 0), method = "L-BFGS-B", hessian = TRUE)
theta <- z$par
loglik <- -z$value
n <- length(x)
I <- z$hessian / n
invI <- solve(I, diag(2L))
dimnames(invI) <- list(c("mu", "sigma2"), c("mu", "sigma2"))
return(list(theta = theta, vcov = invI, loglik = loglik, n = n))
}
}
我们仍然使用之前的数据进行测试:
set.seed(0); x <- rnorm(500)
fit <- fitnormal(x)
hist(x, prob = TRUE)
curve(dnorm(x, fit$theta[1], sqrt(fit$theta[2])), add = TRUE, col = 2)
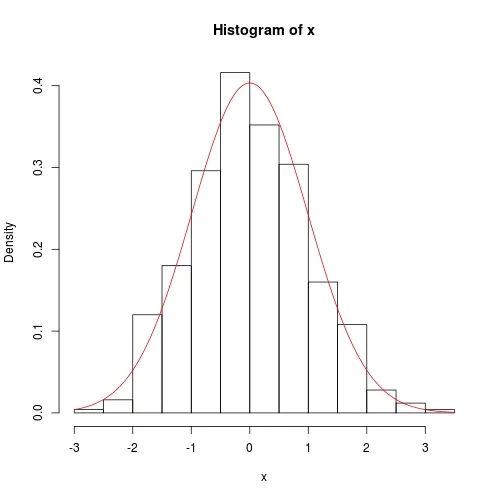
数值方法也相当准确,只是方差协方差矩阵的对角线上并非完全为0:
fitnormal(x, FALSE)
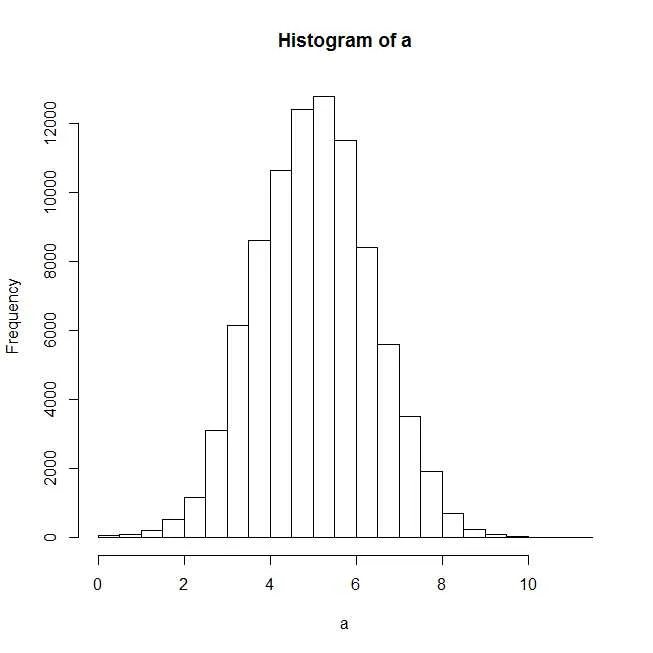





m <- mean(claims); s <- sd(claims)- Hong Ooi