一些帮助渲染曼德博集合的方法

Question

我得到了一些与Mandelbrot集的分形可视化相关的工作。

我并不是在寻求完整的解决方案（当然），我是在寻求关于复数轨道的帮助。

假设我有一个给定的Complex数，它来自于复平面上的一个点。现在我需要迭代它的轨道序列，并根据轨道是否按数量级增加来绘制点。

如何收集一个复数的轨道？任何指导都会受到赞赏（链接等）。任何有关数学函数的指针，例如测试轨道序列所需的Math.pow()

我正在使用Java，但这里并不特别相关。

再次感谢， Alex

- Alex

---

如果您没有数学背景，您可能需要复习一下基本的复数算术。 - Greg Hewgill

Answer 1

当你展示曼德博集合时，你只需将实数和虚数平面分别转换为x和y坐标。

例如，复数4.5 + 0.27i 转换成 x = 4.5，y = 0.27。

曼德博集合是方程Z = Z² + C从未达到|Z| >= 2的所有点，但在实践中，你包括所有值不超过特定迭代次数（例如1000）的点。为了获得通常看到的集合的彩色渲染，你根据它们达到限制的速度为集合外的点分配不同的颜色。

由于涉及到复数，实际上方程是Zr + Zi = (Zr + Zi)² + Cr + Ci。你需要将其分成两个方程，一个用于实数平面，另一个用于虚数平面，然后进行简单的代数运算。C是要测试的点的坐标，Z的初始值为零。

这是我多线程曼德博集合生成器的一张图片：)

- Guffa

---

非常不错。可以看到随着位置接近有界复数，颜色逐渐变亮。 - Alex

Answer 2

实际上，曼德博集合是收敛迭代的复数集合。因此，曼德博集合中唯一的点就是中间的那个无聊的大颜色块。而所有漂亮的颜色只不过是表示边界附近（但错误的一侧）的点向无穷大旋转的速率。用数学术语来说，

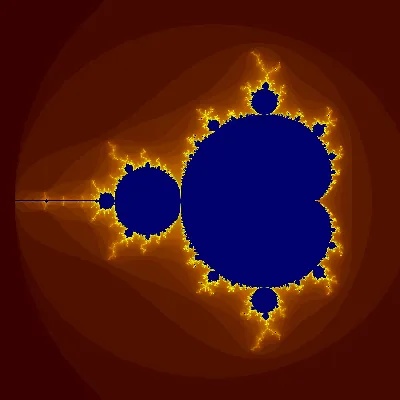
M = {c in C : lim (k -> inf) z_k = 0 } where z_0 = c, z_(k+1) = z_k^2 + c

选择任意一个复数c，要确定它是否在集合中，请重复迭代z_0 = c，z_(k+1) = z_k^2 + c，并且z_k将趋近于零或无穷大。如果它的极限（随着k趋近于无穷大）为零，则它在集合中。否则不在。

可以证明一旦|z_k| > 2，它就不会收敛。这是一个优化练习：如果我没记错，|Z_k|^2 > 2就足够了...无论如何，平方运算将避免使用昂贵的sqrt()函数。

- P i

---

由于集合已经定义，z_0 = 0，这给出了 z_1 = z_0^2 + c = c。 - Guffa

Answer 3

Wolfram Mathworld有一个不错的网站，讲述Mandelbrot集合。

Complex类将非常有帮助。

也许像这个的例子会激发一些思考。我不建议使用Applet。

你必须知道如何对复数进行加、减、乘、除和幂运算，以及正弦、余弦、指数等函数。如果你不知道这些，我建议从那里开始。

我学习的书是Ruel V. Churchill "Complex Variables"。

- duffymo

---

好的，我的r.Max = 2数量级，代表有界值以绘制。轨道值是通过复数算术推导出来的。您知道各种算术运算如何与生成轨道相关联吗？ - Alex

你必须知道如何使用复数进行加、减、乘、除和幂运算，以及诸如正弦、余弦、指数等函数。如果你不了解这些内容，我建议你从这里开始学习。 - duffymo

好的，轨道是复平面上两个复数的乘积P。如果P的阶数大于2与两个复数之和S相比，则它是无界的，因此不属于Mandelbrot集合。这样翻译可以吗？ - Alex

Answer 4

/d{def}def/u{dup}d[0 -185 u 0 300 u]concat/q 5e-3 d/m{mul}d/z{A u m B u
m}d/r{rlineto}d/X -2 q 1{d/Y -2 q 2{d/A 0 d/B 0 d 64 -1 1{/f exch d/B
A/A z sub X add d B 2 m m Y add d z add 4 gt{exit}if/f 64 d}for f 64 div
setgray X Y moveto 0 q neg u 0 0 q u 0 r r r r fill/Y}for/X}for showpage

- DNA