我尝试过许多曼德博集合的绘制算法，包括幼稚的逃逸时间算法以及优化后的逃逸时间算法。但是，有没有更快的算法可以高效地生成像我们在YouTube上看到的那样深入缩放的图像呢？此外，我想了解如何在C/C++ double 之外增加精度的一些想法。
渲染曼德博集合的最快算法是什么？
3
- Vivekanand V
3个回答
4
即使是高端CPU与普通GPU相比仍然会慢得多。即使对于GPU上的朴素迭代算法也可以实现实时渲染。因此，使用更好的GPU算法可以达到更高的缩放级别，但对于任何合理的算法，您需要使用以下内容：
每个高精度值都是
此外，需要选择适当的范围来处理所使用的值的范围，否则将毫无意义。 因此，如果您的数字是小于4，则具有大于10 ^ +5的范围是没有意义的。因此，首先需要确定您拥有的值的边界，然后将其分解为指数范围（每个值的浮点数数量）。
请注意，尽管舍入比本机浮点数少得多，但仍会发生舍入！
现在，在这些数字上执行操作略微比对普通浮点数进行操作更加复杂，因为您需要将每个值处理为所有组件的括号和。
- 多次渲染，因为我们无法在GPU上自我修改纹理
- 高精度浮点数，因为
floats/doubles不足够.
这里有一些相关的问题和答案:
这些可能会让你入门...
其中一种加速方式是，您可以像我在第一个链接中所做的那样使用分数逃逸。它可以在保持最大迭代次数低的同时改善图像质量。
第二个链接将为您提供有关分形哪些部分在内部和外部以及距离有多远的近似值。它不是非常精确，但可以用于避免计算"明确在外面"的部分的迭代。
下一个链接将向您展示如何实现更好的精度。
最后一个链接是关于微扰。其思想是只针对某些参考点使用高精度数学，然后使用低精度数学计算其相邻点，而不会失去精度。我从未使用过它，但看起来很有前途。
最后一步是，一旦您实现了快速渲染，您可能希望瞄准这个:
这里是GLSL中单个值使用3个64位双精度的小例子：
// high precision float (very slow)
dvec3 fnor(dvec3 a)
{
dvec3 c=a;
if (abs(c.x)>1e-5){ c.y+=c.x; c.x=0.0; }
if (abs(c.y)>1e+5){ c.z+=c.y; c.y=0.0; }
return c;
}
double fget(dvec3 a){ return a.x+a.y+a.z; }
dvec3 fset(double a){ return fnor(dvec3(a,0.0,0.0)); }
dvec3 fadd(dvec3 a,double b){ return fnor(a+fset(b)); }
dvec3 fsub(dvec3 a,double b){ return fnor(a-fset(b)); }
dvec3 fmul(dvec3 a,double b){ return fnor(a*b); }
dvec3 fadd(dvec3 a,dvec3 b){ return fnor(a+b); }
dvec3 fsub(dvec3 a,dvec3 b){ return fnor(a-b); }
dvec3 fmul(dvec3 a,dvec3 b)
{
dvec3 c;
c =fnor(a*b.x);
c+=fnor(a*b.y);
c+=fnor(a*b.z);
return fnor(c);
}
每个高精度值都是
dvec3... fnor中的阈值可以更改为任何范围。您可以将此转换为vec3和float。
[Edit1]“快速”C++示例
我想尝试我的新SSD1306驱动程序以及我的AVR32 MCU来计算Mandelbrot，以便我可以与这个Arduino + 3D + Pong + Mandelbrot进行速度比较。我使用带有~66MHz无FPU无GPU和128x64x1bpp显示器的AT32UC3A3256。没有外部存储器，只有内部16 + 32 + 32 KByte。 Naive Mandlebrot 太慢了（每帧约2.5秒），所以我做了一些像这样的事情（利用视图的位置和缩放是连续的特点）：
- 将分辨率降低2倍
- 根据缩放使用可变的最大迭代次数
n - 记住上一帧，以及哪个
x,y屏幕坐标映射到哪个Mandelbrot坐标。 - 在每个帧上，计算屏幕坐标与Mandelbrot坐标之间的映射。
- 调整上一帧以适应新的位置和缩放
所以只需查看#3,#4中的数据，如果我们在上一个和实际帧中有相同的位置（更接近像素大小的一半），则复制像素。并重新计算其余部分。
如果您的视图平滑（因此每帧基础上的位置和缩放不会变化很多），这将极大地提高性能。
为了腐蚀我的输出，因为它只是B&W
更改n会使上一帧无效，以强制重新计算。我知道这很慢，但它仅在缩放范围之间的转换时发生3次。
缩放上一帧的计数不太好看，因为它不是线性的。
可以使用最后的计数，但是这需要记住用于迭代的复杂变量，并且会占用太多内存。
//---------------------------------------------------------------------------
//--- Fast Mandelbrot set ver: 1.000 ----------------------------------------
//---------------------------------------------------------------------------
template<int xs,int ys,int sh> void mandelbrot_draw(float mx,float my,float zoom)
{
// xs,ys - screen resolution
// sh - log2(pixel_size) ... dithering pixel size
// mx,my - Mandelbrot position (center of view) <-1.5,+0.5>,<-1.0,+1.0>
// zoom - zoom
// ----------------
// (previous/actual) frame
static U8 p[xs>>sh][ys>>sh]; // intensities (raw Mandelbrot image)
static int n0=0; // max iteraions
static float px[(xs>>sh)+1]={-1000.0}; // pixel x position in Mandlebrot
static float py[(ys>>sh)+1]; // pixel y position in Mandlebrot
// temp variables
U8 shd; // just pattern for dithering
int ix,iy,i,n,jx,jy,kx,ky,sz; // index variables
int nx=xs>>sh,ny=ys>>sh; // real Mandelbrot resolution
float fx,fy,fd; // floating Mandlebrot position and pixel step
float x,y,xx,yy,q; // Mandelbrot iteration stuff (this need to be high precision)
int qx[xs>>sh],qy[ys>>sh]; // maping of pixels between last and actual frame
float px0[xs>>sh],py0[ys>>sh]; // pixel position in Mandlebrot from last frame
// init vars
if (zoom< 10.0) n= 31;
else if (zoom< 100.0) n= 63;
else if (zoom< 1000.0) n=127;
else n=255;
sz=1<<sh;
ix=xs; if (ix>ys) ix=ys; ix/=sz;
fd=2.0/(float(ix-1)*zoom);
mx-=float(xs>>(1+sh))*fd;
my-=float(ys>>(1+sh))*fd;
// init buffers
if ((px[0]<-999.0)||(n0!=n))
{
n0=n;
for (ix=0;ix<nx;ix++) px[ix]=-999.0;
for (iy=0;iy<ny;iy++) py[iy]=-999.0;
for (ix=0;ix<nx;ix++)
for (iy=0;iy<ny;iy++)
p[ix][iy]=0;
}
// store old and compute new float positions of pixels in Mandelbrot to px[],py[],px0[],py0[]
for (fx=mx,ix=0;ix<nx;ix++,fx+=fd){ px0[ix]=px[ix]; px[ix]=fx; qx[ix]=-1; }
for (fy=my,iy=0;iy<ny;iy++,fy+=fd){ py0[iy]=py[iy]; py[iy]=fy; qy[iy]=-1; }
// match old and new x coordinates to qx[]
for (ix=0,jx=0;(ix<nx)&&(jx<nx);)
{
x=px[ix]; y=px0[jx];
xx=(x-y)/fd; if (xx<0.0) xx=-xx;
if (xx<=0.5){ qx[ix]=jx; px[ix]=y; }
if (x<y) ix++; else jx++;
}
// match old and new y coordinates to qy[]
for (ix=0,jx=0;(ix<ny)&&(jx<ny);)
{
x=py[ix]; y=py0[jx];
xx=(x-y)/fd; if (xx<0.0) xx=-xx;
if (xx<=0.5){ qy[ix]=jx; py[ix]=y; }
if (x<y) ix++; else jx++;
}
// remap p[][] by qx[]
for (ix=0,jx=nx-1;ix<nx;ix++,jx--)
{
i=qx[ix]; if ((i>=0)&&(i>=ix)) for (iy=0;iy<ny;iy++) p[ix][iy]=p[i][iy];
i=qx[jx]; if ((i>=0)&&(i<=jx)) for (iy=0;iy<ny;iy++) p[jx][iy]=p[i][iy];
}
// remap p[][] by qy[]
for (iy=0,jy=ny-1;iy<ny;iy++,jy--)
{
i=qy[iy]; if ((i>=0)&&(i>=iy)) for (ix=0;ix<nx;ix++) p[ix][iy]=p[ix][i];
i=qy[jy]; if ((i>=0)&&(i<=jy)) for (ix=0;ix<nx;ix++) p[ix][jy]=p[ix][i];
}
// Mandelbrot
for (iy=0,ky=0,fy=py[iy];iy<ny;iy++,ky+=sz,fy=py[iy]) if ((fy>=-1.0)&&(fy<=+1.0))
for (ix=0,kx=0,fx=px[ix];ix<nx;ix++,kx+=sz,fx=px[ix]) if ((fx>=-1.5)&&(fx<=+0.5))
{
// invalid qx,qy ... recompute Mandelbrot
if ((qx[ix]<0)||(qy[iy]<0))
{
for (x=0.0,y=0.0,xx=0.0,yy=0.0,i=0;(i<n)&&(xx+yy<4.0);i++)
{
q=xx-yy+fx;
y=(2.0*x*y)+fy;
x=q;
xx=x*x;
yy=y*y;
}
i=(16*i)/(n-1); if (i>16) i=16; if (i<0) i=0;
i=16-i; p[ix][iy]=i;
}
// use stored intensity
else i=p[ix][iy];
// render point with intensity i coresponding to ix,iy position in map
for (i<<=3 ,jy=0;jy<sz;jy++)
for (shd=shade8x8[i+(jy&7)],jx=0;jx<sz;jx++)
lcd.pixel(kx+jx,ky+jy,shd&(1<<(jx&7)));
}
}
//---------------------------------------------------------------------------
//---------------------------------------------------------------------------
//---------------------------------------------------------------------------
这个与lcd和shade8x8相关的内容可以在链接的SSD1306 QA中找到。不过你可以忽略它，因为它只是抖动并输出像素，所以你可以直接输出i（即使没有缩放到<0..16>）。
预览如下（在PC上，因为我懒得连接相机...）：
因此，64x32的曼德博集像素显示为128x64的抖动图像。在我的AVR32上，这可能比朴素方法快8倍（也许是3-4fps）... 代码可能更优化，但请注意曼德博集不是唯一在运行的东西，因为我有一些ISR处理程序在后台处理LCD，还有我的TTS引擎基于此，我自那以来大量升级了它，并用于调试（是的，它可以同时说话和渲染）。另外，我内存不够用，因为我的3D引擎需要占用很多 ~11 KByte的空间（主要是深度缓冲区）。
这是预览代码（在计时器内部）：
static float zoom=1.0;
mandelbrot_draw<128,64,1>(+0.37,-0.1,zoom);
zoom*=1.02; if (zoom>100000) zoom=1.0;
对于非 AVR32 C++ 环境，请使用以下内容：
//------------------------------------------------------------------------------------------
#ifndef _AVR32_compiler_h
#define _AVR32_compiler_h
//------------------------------------------------------------------------------------------
typedef int32_t S32;
typedef int16_t S16;
typedef int8_t S8;
typedef uint32_t U32;
typedef uint16_t U16;
typedef uint8_t U8;
//------------------------------------------------------------------------------------------
#endif
//------------------------------------------------------------------------------------------
[编辑2]在GLSL中提高浮点精度
曼德博集合的主要问题是需要将指数差异非常大的数字相加。对于+，-操作，我们需要对两个操作数的尾数进行对齐，将它们作为整数相加，然后再规范化为科学计数法。然而，如果指数差别很大，那么结果尾数所需的位数就会超过32位浮点数所能容纳的位数，因此只保留24位最高有效位。这样就会产生舍入误差，导致像素化。如果您查看32位float的二进制表示，您将看到以下内容：
float a=1000.000,b=0.00001,c=a+b;
//012345678901234567890123456789 ... just to easy count bits
a=1111101000b // a=1000
b= 0.00000000000000001010011111000101101011b // b=0.00000999999974737875
c=1111101000.00000000000000001010011111000101101011b // not rounded result
c=1111101000.00000000000000b // c=1000 rounded to 24 bits of mantissa
现在的想法是扩大尾数位数。最简单的方法是使用两个浮点数而不是一个：
//012345678901234567890123 ... just to easy count bits
a=1111101000b // a=1000
//012345678901234567890123 ... just to easy count b= 0.0000000000000000101001111100010110101100b // b=0.00000999999974737875
c=1111101000.00000000000000001010011111000101101011b // not rounded result
c=1111101000.00000000000000b // c=1000 rounded to 24
+ .0000000000000000101001111100010110101100b
//012345678901234567890123 ... just to easy count bits
因此，结果的一部分在一个浮点数中，其余部分在另一个浮点数中... 每个单值中的浮点数越多，尾数就越大。但是，在将大尾数精确分成24位块的情况下，在GLSL中执行此操作将会很复杂且速度慢（如果由于GLSL限制可能根本不可能）。相反，我们可以为每个浮点数选择一些指数范围（就像上面的示例一样）。
因此，在这个例子中，对于每个单值（float），我们得到了3个浮点数（vec3）。每个坐标都代表不同的范围：
abs(x) <= 1e-5
1e-5 < abs(y) <= 1e+5
1e+5 < abs(z)
并且 value = (x+y+z)，因此我们有三个 24 位尾数，但是范围并不完全匹配 24 位。为此，指数范围应该被分割为：
log10(2^24)=7.2247198959355486851297334733878
不要使用10...，可以考虑使用类似于以下内容的东西：
abs(x) <= 1e-7
1e-7 < abs(y) <= 1e+0
1e+0 < abs(z)
此外，需要选择适当的范围来处理所使用的值的范围，否则将毫无意义。 因此，如果您的数字是小于4，则具有大于10 ^ +5的范围是没有意义的。因此，首先需要确定您拥有的值的边界，然后将其分解为指数范围（每个值的浮点数数量）。
请注意，尽管舍入比本机浮点数少得多，但仍会发生舍入！
现在，在这些数字上执行操作略微比对普通浮点数进行操作更加复杂，因为您需要将每个值处理为所有组件的括号和。
(x0+y0+z0) + (x1+y1+z1) = (x0+x1 + y0+y1 + z0+z1)
(x0+y0+z0) - (x1+y1+z1) = (x0-x1 + y0-y1 + z0-z1)
(x0+y0+z0) * (x1+y1+z1) = x0*(x1+y1+z1) + y0*(x1+y1+z1) + z0*(x1+y1+z1)
不要忘记将值归一化回定义范围。避免添加小和大的（绝对值）值，因此避免 x0+z0 等...
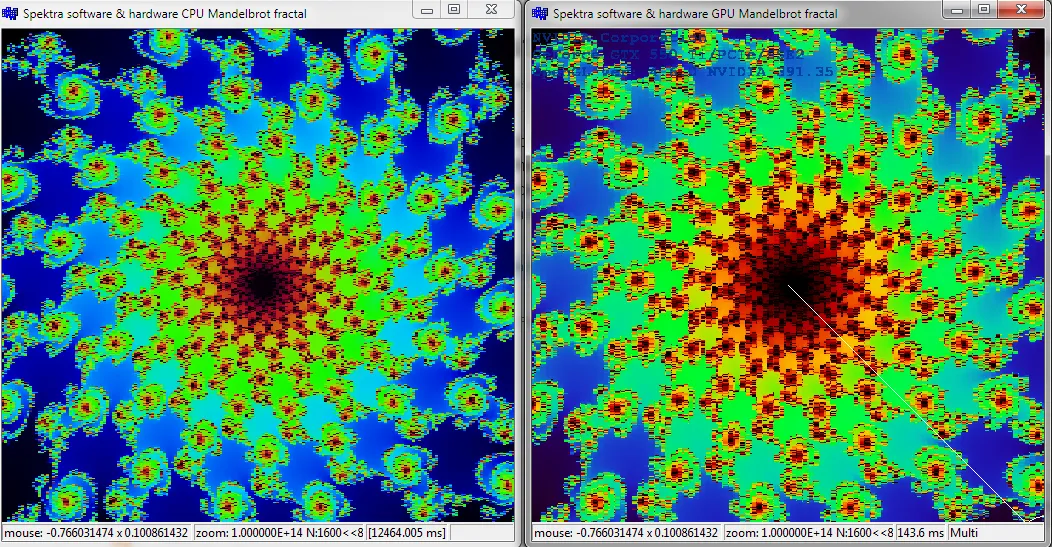
[编辑3]新的win32演示CPU vs.GPU
两个可执行文件都预设到相同的位置和缩放级别，以显示何时开始舍入doubles。我必须稍微升级px,py坐标的计算方式，因为在此位置（阈值仍可能过大）10^9处，y轴开始偏离。
这里是高倍缩放（n=1600）的CPU与GPU预览：
CPU的实时GIF捕获（n=62 ++，GIF 4倍缩小）：
- Spektre
37
2
优化的逃逸算法应该足够快，能够实时绘制Mandelbrot集合。您可以使用多线程，以便您的实现更快（例如，使用OpenMP非常容易）。如果需要，您还可以手动使用SIMD指令对代码进行矢量化，使其更快。如果这仍然不够快，您甚至可以直接在GPU上运行，使用着色器和/或GPU计算框架（OpenCL或CUDA）（尽管这有点复杂，需要高效地完成）。最后，您应该调整迭代次数，使其相对较小。
缩放不应该对性能产生任何直接影响。它只是更改了计算的输入窗口。但是，它确实会产生间接影响，因为实际迭代次数会发生变化。窗口外的点不应计算。
双精度浮点数应该足以正确绘制Mandelbrot集合。但是，如果您确实需要更精确的计算，可以使用双倍精度，这会提供相当不错的精度和性能。然而，手动实现双倍精度有些棘手，而且仍然比只使用双精度慢得多。
缩放不应该对性能产生任何直接影响。它只是更改了计算的输入窗口。但是，它确实会产生间接影响，因为实际迭代次数会发生变化。窗口外的点不应计算。
双精度浮点数应该足以正确绘制Mandelbrot集合。但是，如果您确实需要更精确的计算，可以使用双倍精度，这会提供相当不错的精度和性能。然而，手动实现双倍精度有些棘手，而且仍然比只使用双精度慢得多。
- Jérôme Richard
2
我的最快解决方案是通过跟随轮廓边界和填充来避免迭代相同深度的大区域。可能会有一个惩罚，即可能会剪掉小芽而不是绕过它们，但总的来说，这是为了快速缩放所付出的小代价。
一种可能的效率是，如果缩放使比例翻倍，则已经有1/4的点。
对于动画，我会记录每个帧的值，每次将比例翻倍，并在播放时实时插入中间帧，因此动画每秒钟翻倍一次。 double类型可以存储超过50个关键帧，从而产生持续超过一分钟（进入和退出）的动画。
实际的迭代是通过手工编写的汇编器完成的，因此一个像素完全在FPU中迭代。
- Weather Vane
2
你能否再澄清一下？ - Vivekanand V
我使用“逃逸时间”算法。我尝试过使用“远离曼德博集合”的方法，但是无法超越我提到的三个主要想法：a）重复使用您所知道的内容，b）在可能的情况下避免迭代，c）在亿万次的迭代中，每一个时钟周期都很重要。我不知道是否有非迭代性的解决方案。 - Weather Vane
网页内容由stack overflow 提供, 点击上面的可以查看英文原文，
原文链接
原文链接
C（屏幕上的位置）的计算有关（在顶点/几何体着色器和片段着色器之间的阶段）。因为当我在GPU上实现更高的精度时，像素化没有改变一点。我想尝试在CPU端使用高精度，以验证我的怀疑......但这也可能只是我的实现中的某个错误。是的，GPU很平滑。 - Spektrevec2相比原生浮点数将缩放精度提高到4x，但此后出现了我所谓的“破碎玻璃”像素化...唯一的缺点是，正如我们之前讨论过的那样，我的速度降低了，我必须减半迭代次数才能恢复以前的速度！感谢您的回答:) 但是，仍然有一些概念上的东西，我个人需要理解...对我来说，最初只是曼德博集的简单渲染，现在却带我去了我从未梦想过的地方！ - Vivekanand V