logo标签列表

3D最小二乘平面

algorithmmathstatistics
39

如何在(x, y, z)空间中，基于一组三维数据点计算出最小二乘平面的算法？换言之，如果我有一堆点，例如(1,2,3),(4,5,6),(7,8,9)，那么如何计算最适合的拟合平面f(x,y)=ax+by+c？从一组三维点中获取a、b和c的算法是什么？

3
您应该明确定义“最小二乘”的确切含义。例如，请参考http://en.wikipedia.org/wiki/Least_squares以了解不同的定义方式。 - Jouni K. Seppänen
这是一条注释。如果有人能够将其移动到Stephen Canon答案的评论中，那就太好了。我希望这可以澄清他所说的“解向量的三个分量是最小二乘拟合平面的系数{a，b，c}。” 首先，根据基本矩阵代数，给定Ax = b，其中A是矩阵，b和x是向量，只有当A具有非零行列式时才存在解。这意味着您需要超过3个点，并且至少有一个点不在平面上（不精确）。第二个澄清和原因 - cluless
10个回答
47

如果你有 n 个数据点 (x[i], y[i], z[i])，计算出一个 3x3 对称矩阵 A，其条目为：

sum_i x[i]*x[i],    sum_i x[i]*y[i],    sum_i x[i]
sum_i x[i]*y[i],    sum_i y[i]*y[i],    sum_i y[i]
sum_i x[i],         sum_i y[i],         n

还需要计算三元素向量b：

{sum_i x[i]*z[i],   sum_i y[i]*z[i],    sum_i z[i]}

使用给定的A和b解Ax = b。 解向量的三个分量是最小二乘拟合平面的系数{a，b，c}。

请注意，这是“普通最小二乘”拟合，仅在z预计为x和y的线性函数时才适用。如果您更普遍地寻找三维空间中的“最佳拟合平面”，您可能需要了解“几何”最小二乘。

还要注意，如果您的点在一条直线上，则此方法将失败，就像您的示例点一样。

6
有三种常见方法。你提到的基于奇异值分解的方法对于某些问题是首选，但比我使用的相对简单的“正规方程”方法更难以解释（和理解）。基于奇异值分解的方法实际上比解决正规方程更慢，但更受青睐，因为它更具数值稳定性。 - Stephen Canon
1
如果您想了解所有不同的LLS算法的详细信息，请访问http://en.wikipedia.org/wiki/Linear_least_squares#Orthogonal_decomposition_methods。 - Stephen Canon
2
@AKE：不，当您使用QR或SVD时，您不使用正常方程（意思是您不形成我描述的3x3矩阵，而是直接在测量的nx3矩阵上进行操作）。这会导致更好的稳定性(a)因为正交分解具有良好的稳定性质，更重要的是(b)因为XtX的条件数是X的条件数的平方。 - Stephen Canon
1
我在哪里可以找到这种方法的解释，特别是矩阵是如何构造的以及为什么解向量等于平面系数？我看了维基百科的文章，但它只涉及非常一般的方程，对我并没有太大帮助。 - Adrian17
2
我认为你可以在这篇文章中找到一些解释 http://www.ilikebigbits.com/blog/2015/3/2/plane-from-points - Jayesh
显示剩余9条评论
16

平面方程为：ax + by + c = z。因此，使用所有数据设置如下矩阵：

    x_0   y_0   1  
A = x_1   y_1   1  
          ... 
    x_n   y_n   1

和
    a  
x = b  
    c

并且

    z_0   
B = z_1   
    ...   
    z_n

换句话说，Ax = B。现在求解x，它是你的系数。但由于（我假定）你有超过3个点，所以该系统已经超定，因此您需要使用左伪逆。因此答案是：
a 
b = (A^T A)^-1 A^T B
c

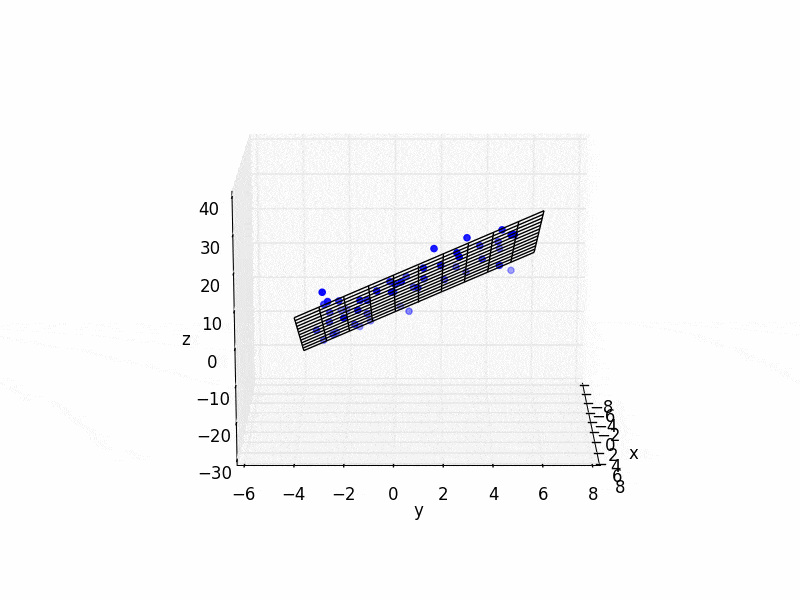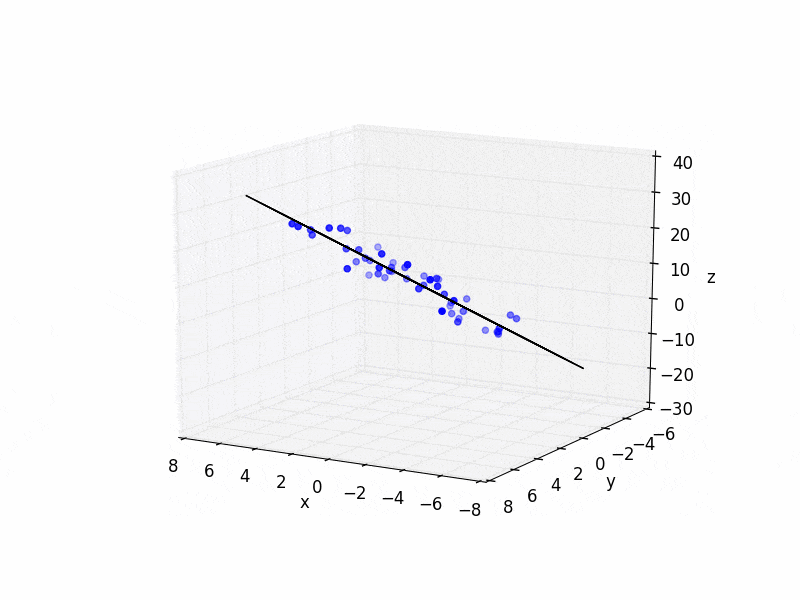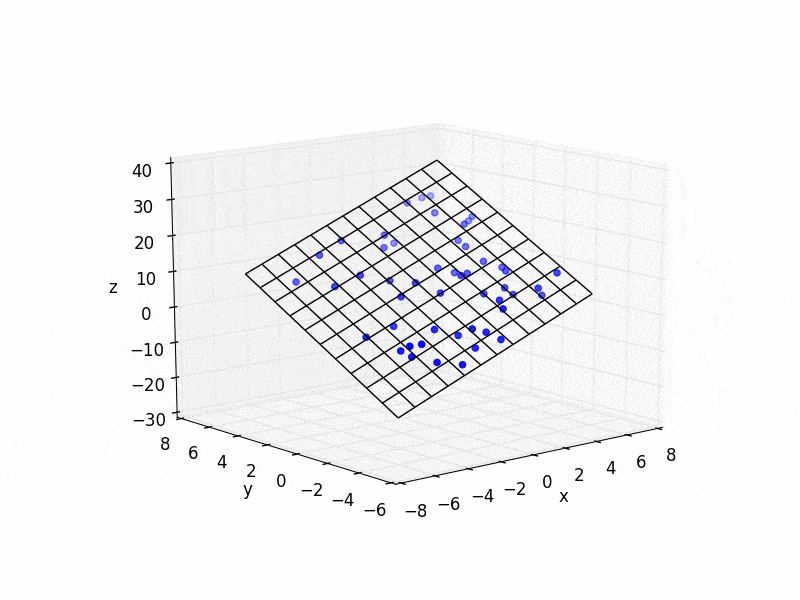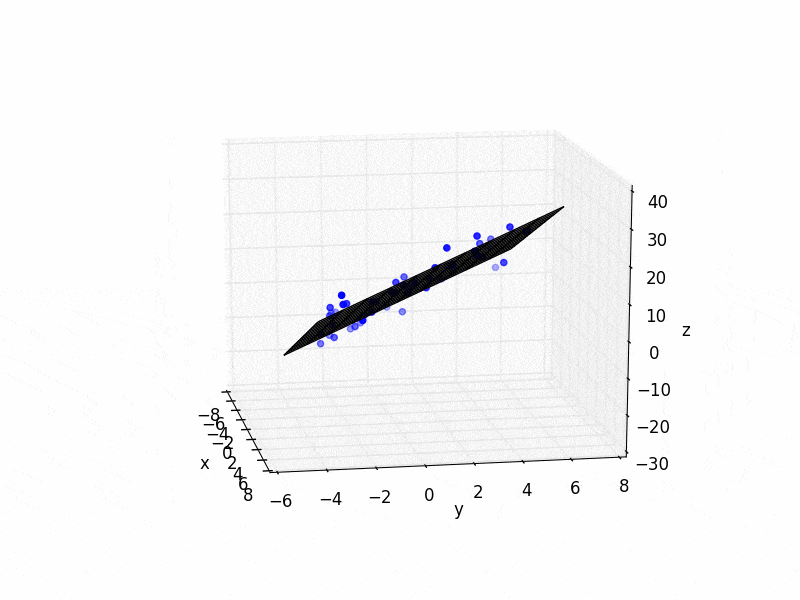
以下是一个简单的Python代码示例：

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

N_POINTS = 10
TARGET_X_SLOPE = 2
TARGET_y_SLOPE = 3
TARGET_OFFSET  = 5
EXTENTS = 5
NOISE = 5

# create random data
xs = [np.random.uniform(2*EXTENTS)-EXTENTS for i in range(N_POINTS)]
ys = [np.random.uniform(2*EXTENTS)-EXTENTS for i in range(N_POINTS)]
zs = []
for i in range(N_POINTS):
    zs.append(xs[i]*TARGET_X_SLOPE + \
              ys[i]*TARGET_y_SLOPE + \
              TARGET_OFFSET + np.random.normal(scale=NOISE))

# plot raw data
plt.figure()
ax = plt.subplot(111, projection='3d')
ax.scatter(xs, ys, zs, color='b')

# do fit
tmp_A = []
tmp_b = []
for i in range(len(xs)):
    tmp_A.append([xs[i], ys[i], 1])
    tmp_b.append(zs[i])
b = np.matrix(tmp_b).T
A = np.matrix(tmp_A)
fit = (A.T * A).I * A.T * b
errors = b - A * fit
residual = np.linalg.norm(errors)

print("solution:")
print("%f x + %f y + %f = z" % (fit[0], fit[1], fit[2]))
print("errors:")
print(errors)
print("residual:")
print(residual)

# plot plane
xlim = ax.get_xlim()
ylim = ax.get_ylim()
X,Y = np.meshgrid(np.arange(xlim[0], xlim[1]),
                  np.arange(ylim[0], ylim[1]))
Z = np.zeros(X.shape)
for r in range(X.shape[0]):
    for c in range(X.shape[1]):
        Z[r,c] = fit[0] * X[r,c] + fit[1] * Y[r,c] + fit[2]
ax.plot_wireframe(X,Y,Z, color='k')

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()

fitted plane

如果xs = [] ys = [] zs = [] 则会出现“奇异矩阵”错误： 对于i在N_POINTS范围内，执行以下操作： xs.append(i * i) ys.append(0) zs.append(1) - Alexey
@Alexey，你输入的点在一条直线上。因此有无数个平面可以完美匹配数据。这是一个退化情况，最小二乘法解决不了。实际上，我不确定任何通用解决方案都可以解决它。如果你有具体问题，请开一个新的问题，可能引用这个问题。 - Ben
嗨Ben，谢谢你。你能否提供一个链接/文本来解释一下你是如何从“ax + by + dz + c = 0”到“ax + by + c = z”的？你不是假设平面法线的z分量总是为1吗？ - Pe Dro
在线性代数中，与普通代数一样，您可以从方程两边减去 z 以使一侧为零。该网站不支持 MathJax。也许在这里更清楚。 - Ben
5

除非有人告诉我如何在此处输入等式，否则让我只写下您需要进行的最终计算：

首先，给定点r_i \n \R，i = 1..N，计算所有点的质心：

r_G = \frac{\sum_{i=1}^N r_i}{N}

接下来，通过计算3x3矩阵A来计算法向量n，它与基向量r_G一起定义了平面。

A = \sum_{i=1}^N (r_i - r_G)(r_i - r_G)^T

有了这个矩阵，法线向量n现在由A的对应于最小特征值的特征向量给出。

要了解特征向量/特征值对，请使用您选择的任何线性代数库。

此解决方案基于Hermitian矩阵A的Rayleight-Ritz定理。

你能告诉我你从哪里得到的吗？我看不出与瑞利-里茨定理有什么联系。 - Markus Hütter
@josch 这里没有LaTeX。请参阅https://meta.stackexchange.com/questions/30559/latex-on-stack-overflow - Nathan majicvr.com
5

请参考David Eberly的“数据最小二乘拟合”来了解我是如何得出这个结果的，以最小化几何拟合（点到平面的正交距离）。

bool Geom_utils::Fit_plane_direct(const arma::mat& pts_in, Plane& plane_out)
{
    bool success(false);
    int K(pts_in.n_cols);
    if(pts_in.n_rows == 3 && K > 2)  // check for bad sizing and indeterminate case
    {
        plane_out._p_3 = (1.0/static_cast<double>(K))*arma::sum(pts_in,1);
        arma::mat A(pts_in);
        A.each_col() -= plane_out._p_3; //[x1-p, x2-p, ..., xk-p]
        arma::mat33 M(A*A.t());
        arma::vec3 D;
        arma::mat33 V;
        if(arma::eig_sym(D,V,M))
        {
            // diagonalization succeeded
            plane_out._n_3 = V.col(0); // in ascending order by default
            if(plane_out._n_3(2) < 0)
            {
                plane_out._n_3 = -plane_out._n_3; // upward pointing
            }
            success = true;
        }
    }
    return success;
}

在 Windows 7、i7、32位程序环境下，对1000个点拟合平面所需时间为37微秒。

enter image description here

4
这可以简化为总最小二乘问题，可以使用SVD分解来解决。
使用OpenCV的C++代码：
float fitPlaneToSetOfPoints(const std::vector<cv::Point3f> &pts, cv::Point3f &p0, cv::Vec3f &nml) {
    const int SCALAR_TYPE = CV_32F;
    typedef float ScalarType;

    // Calculate centroid
    p0 = cv::Point3f(0,0,0);
    for (int i = 0; i < pts.size(); ++i)
        p0 = p0 + conv<cv::Vec3f>(pts[i]);
    p0 *= 1.0/pts.size();

    // Compose data matrix subtracting the centroid from each point
    cv::Mat Q(pts.size(), 3, SCALAR_TYPE);
    for (int i = 0; i < pts.size(); ++i) {
        Q.at<ScalarType>(i,0) = pts[i].x - p0.x;
        Q.at<ScalarType>(i,1) = pts[i].y - p0.y;
        Q.at<ScalarType>(i,2) = pts[i].z - p0.z;
    }

    // Compute SVD decomposition and the Total Least Squares solution, which is the eigenvector corresponding to the least eigenvalue
    cv::SVD svd(Q, cv::SVD::MODIFY_A|cv::SVD::FULL_UV);
    nml = svd.vt.row(2);

    // Calculate the actual RMS error
    float err = 0;
    for (int i = 0; i < pts.size(); ++i)
        err += powf(nml.dot(pts[i] - p0), 2);
    err = sqrtf(err / pts.size());

    return err;
}
conv 函数是什么？它不是 OpenCV 的函数，对吧？ - Szymon Bednorz
没错，我不认为这是OpenCV的问题。这只是从Point3f转换为Vec3f，就像减去cv::Point3f(0,0,0)一样。 - Michael Litvin
2
2
与任何最小二乘法一样，您可以按照以下步骤进行：

开始编码前

  1. 写出平面的某种参数化方程，比如在三个参数中写成0 = ax + by + z + d。

  2. 找到一个表达式D(\vec{v};a, b, d)，表示任意点\vec{v}到该平面的距离。

  3. 写出求和式S = \sigma_i=0,n D^2(\vec{x}_i)，并简化它，使其用v的各分量的简单求和来表示，例如\sigma v_x，\sigma v_y^2，\sigma v_x*v_z等。

  4. 写出每个参数的最小化表达式dS/dx_0 = 0，dS/dy_0 = 0 ... 这给出了一个由三个参数和前一步的求和组成的三个方程组。

  5. 解这组方程得到参数。

（或者对于简单情况，只需查找表格）。使用符号代数软件包（如Mathematica）可以使您的生活更轻松。

编码

  • 编写代码以形成所需的总和，并从上面的最后一组中找到参数。

替代方案

请注意，如果您实际上只有三个点，则最好找到通过它们的平面。

此外，如果解析解不可行（对于平面不是这种情况，但一般可能存在），则可以执行步骤1和2，并在步骤3中使用Monte Carlo minimizer。

请考虑将未解析的LaTex代码更改为更易读的形式。 - Pe Dro
1

听起来你只是想用两个自变量进行线性回归。维基百科页面上的内容应该能告诉你所需的一切，甚至更多。

0

你需要做的就是解决这个方程组。

如果这些是你的点： (1, 2, 3), (4, 5, 6), (7, 8, 9)

那么你可以得到以下方程：

3=a*1 + b*2 + c
6=a*4 + b*5 + c
9=a*7 + b*8 + c

所以你的问题实际上应该是：如何解决一组方程？

因此，我建议阅读this这个SO问题。

如果我误解了你的问题，请告诉我们。

编辑：

请忽略我的答案，因为你可能想问其他问题。

3
该示例不好，因为OP给出了三个点，但他想要解决一般情况，即给定n个点和一个超约束系统。如果不是所有的点都在一个平面上，他想要找到最佳拟合平面，即在最小二乘意义下使所有点到平面的距离最小化的平面。 - Daniel Brückner
0

我们首先提出了一种线性最小二乘平面拟合方法，该方法最小化估计法向量与提供的点之间的残差。

回想一下，通过原点的平面方程是Ax + By + Cz = 0，其中（x，y，z）可以是平面上的任意一点，（A，B，C）是垂直于该平面的法向量。

一般平面（可能通过原点或不通过原点）的方程是Ax + By + Cz + D = 0，其中附加系数D表示平面沿着法向量方向离原点有多远。【请注意，在此方程中，（A，B，C）形成一个单位法向量。】

现在，我们可以在这里应用一个技巧，并仅使用提供的点坐标来拟合平面。将两侧都除以D并将此项重新排列到右侧。这导致A/D x + B/D y + C/D z = -1。【请注意，在此方程中，（A/D，B/D，C/D）形成长度为1/D的法向量。】

我们可以相应地建立一个线性方程组，然后通过C++中的Eigen求解器解决它，如下所示。

// Example for 5 points
Eigen::Matrix<double, 5, 3> matA; // row: 5 points; column: xyz coordinates
Eigen::Matrix<double, 5, 1> matB = -1 * Eigen::Matrix<double, 5, 1>::Ones();

// Find the plane normal
Eigen::Vector3d normal = matA.colPivHouseholderQr().solve(matB);

// Check if the fitting is healthy
double D = 1 / normal.norm();
normal.normalize(); // normal is a unit vector from now on
bool planeValid = true;
for (int i = 0; i < 5; ++i) { // compare Ax + By + Cz + D with 0.2 (ideally Ax + By + Cz + D = 0)
  if ( fabs( normal(0)*matA(i, 0) + normal(1)*matA(i, 1) + normal(2)*matA(i, 2) + D) > 0.2) {
    planeValid = false; // 0.2 is an experimental threshold; can be tuned
    break;
  }
}

我们随后讨论它与典型的基于SVD的方法的等价性及其比较。

上述线性最小二乘（LLS）方法适用于拟合一般平面方程Ax + By + Cz + D = 0，而基于SVD的方法将D替换为D = - (Ax0 + By0 + Cz0)，并拟合平面方程A(x-x0) + B(y-y0) + C(z-z0) = 0，其中(x0，y0，z0)是所有点的平均值，作为新局部坐标系的原点。

两种方法之间的比较：

  • LLS拟合方法比基于SVD的方法快得多，并且适用于已知点大致处于平面形状的情况。
  • 当平面远离原点时，基于SVD的方法在数值上更稳定，因为在这种情况下，LLS方法需要存储和处理更多小数位数。
  • LLS方法可以通过检查每个点与估计法向量之间的点积残差来检测异常值，而基于SVD的方法可以通过检查协方差矩阵的最小特征值是否显着小于两个较大特征值（即检查协方差矩阵的形状）来检测异常值。

我们最终提供了一个C++和MATLAB的测试用例。

// Test case in C++ (using LLS fitting method)
matA(0,0) = 5.4637; matA(0,1) = 10.3354; matA(0,2) = 2.7203;
matA(1,0) = 5.8038; matA(1,1) = 10.2393; matA(1,2) = 2.7354;
matA(2,0) = 5.8565; matA(2,1) = 10.2520; matA(2,2) = 2.3138;
matA(3,0) = 6.0405; matA(3,1) = 10.1836; matA(3,2) = 2.3218;
matA(4,0) = 5.5537; matA(4,1) = 10.3349; matA(4,2) = 1.8796;
// With this sample data, LLS fitting method can produce the following result
// fitted normal vector = (-0.0231143, -0.0838307, -0.00266429)
// unit normal vector = (-0.265682, -0.963574, -0.0306241)
// D = 11.4943


% Test case in MATLAB (using SVD-based method)
points = [5.4637 10.3354 2.7203;
          5.8038 10.2393 2.7354; 
          5.8565 10.2520 2.3138; 
          6.0405 10.1836 2.3218; 
          5.5537 10.3349 1.8796]
covariance = cov(points)
[V, D] = eig(covariance)
normal = V(:, 1) % pick the eigenvector that corresponds to the smallest eigenvalue
% normal = (0.2655, 0.9636, 0.0306)
网页内容由stack overflow 提供, 点击上面的
可以查看英文原文，
原文链接