分段最小二乘法的动态规划算法

Question

我已经试图在Python中实现这个算法几天了。我一直回过头来，然后就放弃了，感到沮丧。我不知道发生了什么。我没有人可以问，也没有地方可以寻求帮助，所以我来到这里。 Mahesh Viswanathan - CS 473ug: Algorithms - Dynamic Programming PDF警告：http://www.cs.uiuc.edu/class/sp08/cs473/Lectures/lec10.pdf 我觉得这个解释不够清楚，我确实不理解。

我对发生的事情的理解是这样的：

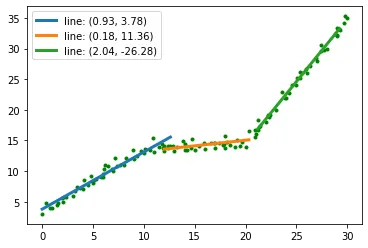
我们有一组点(x1,y1)，(x2,y2)..，我们想要找到最适合这些数据的一些直线。我们可以有多条直线，这些直线来自给定的a和b的公式(y = ax + b)。

现在算法从末尾开始（？），假设点p（x_i，y_i）是线段的一部分。然后笔记中提到最优解是“对于{p1，... pi−1}的最优解加上通过{pi，... pn}的（最佳）直线”。对我来说，这意味着我们到达点p（x_i，y_i），然后向后找到另一条通过其余点的线段。现在最优解是这两个线段的组合。

然后它进行了一个我无法理解的逻辑跳跃，并说“假设最后一个点pn是从p_i开始的一段的一部分。如果Opt（j）表示前j个点的成本，e（j，k）表示通过点j到k的最佳直线的误差，那么Opt（n）= e（i，n）+ C + Opt（i−1）”。

然后是算法的伪代码，我不理解。我知道我们想要遍历点列表并找到最小化OPT（n）公式的点，但我就是不明白。这让我感觉很愚蠢。

我知道这个问题很烦人，而且不容易回答，但我只是想寻求一些指导，以便理解这个算法。对于使用PDF的不便，我表示歉意，但我没有更好的方法将关键信息传达给读者。

感谢您花时间阅读这篇文章，我非常感激。

- gurk

---

链接的文档包含许多算法。你在看哪一个？ - pyfunc

@pyfunc：分段最小二乘法。第49/80页。我相信您可以在右侧边栏下方点击“最小分段平方”，它也会带您到那里。 - gurk

有趣的是，这个算法是由贝尔曼提出的，已经有大约50年的历史了，可能是动态规划的第一个公开示例。 - piccolbo

有没有更新的链接的机会？或者有没有关键词可以找到它？ - undefined

Answer 1

最小二乘问题旨在找到一个最佳拟合给定点的单条线，并有一个优美的闭合形式解决方案。这个解决方案被用作解决分段最小二乘问题的原语。

在分段最小二乘问题中，我们可以有任意数量的段来适应给定的点，并且我们必须为使用每个新段支付成本。如果使用新段的成本为0，则可以通过穿过每个点的单独直线完全拟合所有点。

现在假设我们正在尝试找到最适合n个给定点的分段集。如果我们知道n-1个子问题的最佳解：第一个点的最佳适配，前两个点的最佳适配，......前n-1个点的最佳适配，则我们可以计算出带n个点的原始问题的最佳解决方案如下：

第n个点位于单个线段上，该线段从一些早期点i开始，其中i = 1、2、...、n。我们已经解决了所有较小的子问题，即少于n个点，因此我们可以找到最适合n个点的最佳拟合，使得以下最小化：

最佳适配费用的前i-1个点（已计算）+ 最适合点i到n的单条线的成本（使用最小二乘问题）+ 使用新段的成本

最小化上述数量的值给出了解决方案：使用子问题i-1的最佳适配和通过点i到n的线段。

如果需要更多帮助，我已经在这里写了算法的解释并提供C ++实现：http：//kartikkukreja.wordpress.com/2013/10/21/segmented-least-squares-problem/

- Kartik Kukreja

---

这是2019年。但是您的帖子对我理解这个算法非常有帮助。 - dev_nut

Answer 2

需要注意的是，动态规划部分是较为棘手的部分。

for j = 1 to n
    M[j] = min_(1=<i=<j) ( e(i,j) + C + M[i-1])

在此之前，已经执行了 M[0] = 0 的操作，n 是数据点的总数。下划线表示括号中的部分应该是下标。教授可能会使用 OPT 而不是 M，在其他一些大学关于此问题的讲座中也是如此，您可以在网上找到这些课程（它们看起来几乎相同）。现在，如果您查看我的代码块和讲座中的代码块，您会注意到一个区别。我使用了 M[i-1]，而您的教授使用了 M[j-1]。这是您教授伪代码中的一个打字错误。您甚至可以回头看一下之前的幻灯片，看到他在那里的错误函数中是正确的。

基本上，对于每个 j，您都在寻找从 i 绘制到 j 的点，使得它的误差加上添加这条额外线的成本（C）以及使所有线段直到 i（已经选择最佳）的成本最小化。

还要记住，e(i,i) = 0 以及 e(i,i+1)，因为将一条线拟合到一个点既没有误差，也没有拟合到两个点。

- Justin Peel

---

这是一个不错的小算法，所以我使用numpy自己尝试了一下。它似乎在工作，如果您有进一步的问题，请告诉我。 - Justin Peel

Answer 3

从点1开始，到点j的最佳解决方案必须包括新的终点j在最后一条线段中，因此问题变成了我必须将最后一个分割放在哪里以最小化这个最后一条线段的成本？

幸运的是，成本是根据您正在尝试解决的相同问题的子问题计算的，而且幸运的是，当您移动到下一个点j时，您已经通过解决这些较小的子问题来解决了它们。因此，在新的点j处，您正在尝试找到一个最优点i，在点1和j之间，以分离包括j的新线段，并最小化成本：optimal_cost_up_to(i) + cost_of_split + cost_of_lsq_fit(i+1,j)。现在令人困惑的部分是，在任何时候，它可能看起来像您只是在寻找单个分割，但实际上所有先前的分割都由optimal_cost_up_to(i)确定，而且由于您已经计算出了导致j的所有这些点的最优成本，那么您只需要记忆答案，以便算法不必每次推进一个点时重新计算这些成本。

在Python中，我可能会使用字典来存储结果，尽管对于这种动态编程算法，数组可能更好...

无论如何...

    def optimalSolution(points,split_cost)
        solutions = {0:{'cost':0,'splits':[]}}
        for j in range(1,len(points)):
            best_split = None
            best_cost = lsqFitCost(points,0,j)
            for i in range(0,j):
                cost = solutions[i]['cost'] + split_cost + lsqFitCost(points,i+1,j)
                if cost < best_cost:
                   best_cost = cost
                   best_split = i
            if best_split != None:
                solution[j] = {'cost':best_cost,'splits':solution[best_split]['splits']+[best_split]}
            else:
                solution[j] = {'cost':best_cost,'splits':[]}
        return solutions

这不是很漂亮，而且我还没有检查它（可能存在没有分割是最佳成本的情况错误），但希望它能帮助您找到正确的路径？请注意，lsqFitCost在每次迭代中必须执行大量工作，但对于像这样的最小二乘线拟合，您可以通过维护用于计算的运行总和来使此成本大大降低...您应该谷歌最小二乘线拟合以获取更多信息。这可以使lsqFitCost恒定，因此总时间将为O（N ^ 2）。

- Cyclone

Answer 4

以下是分段最小二乘问题的动态规划公式：

这里，M[j]代表在点i到j上拟合的最小误差（回归）线，我们可以通过在动态规划数组中保持一个反向指针数组来追踪具有最小误差（MSE）的起始点i。此外，c表示绘制一条线的成本（作为适合线条数量的惩罚）。最优子结构特性由贝尔曼方程给出。

以下是我对上述DP算法的Python实现，应用于以下带有点（xs，ys）的2D数据集（如下图所示）：

def ls_fit(xs, ys, m):
    a = (m*sum(xs*ys)-sum(xs)*sum(ys)) / (m*sum(xs**2)-sum(xs)**2)
    b = (sum(ys)-a*sum(xs)) / m
    return a, b

def compute_errors(xs, ys):
    n = len(xs)
    e = np.zeros((n,n))
    for j in range(n):
        for i in range(j+1):
            m = j-i+1
            if m > 1:
                a, b = ls_fit(xs[i:i+m], ys[i:i+m], m)
                e[i,j] = sum((ys[i:i+m] - a*xs[i:i+m] - b)**2)
    return e

def build_DP_table(e, n):
    M = np.zeros(n)
    p = np.zeros(n, dtype=int) # backpointers
    for j in range(1, n):
        cost = [e[i,j] + c + M[i-1] for i in range(j)]
        M[j] = np.min(cost)
        p[j] = np.argmin(cost)
    return M, p

现在绘制使用动态规划公式获得的最小二乘线段：

c = 10
tol = 2
starts = np.unique(p)
drawn = set([])
plt.plot(xs, ys, 'g.')
for start in starts:
    indices = np.where(abs(p-start) < tol)[0]
    a, b = ls_fit(xs[indices], ys[indices], len(indices))
    if not (a, b) in drawn:
        plt.plot([xs[min(indices)],xs[max(indices)]], [a*xs[min(indices)]+b, a*xs[max(indices)]+b], linewidth=3, 
                 label='line: ({:.2f}, {:.2f})'.format(a,b))
        drawn.add((a,b))
plt.legend()

正如预期的那样，DP 找到了最优的 3 条最小二乘线 (L=3) 并将其拟合到数据上。

- Sandipan Dey

---

你有那些幻灯片的链接吗？ - undefined

Answer 5

动态规划的基本原则是在递归地优化问题（降低“成本”或在此情况下降低误差）的同时存储子问题的成本，因此不需要重新计算这些成本（这称为内存化）。由于其“分割”的特点，因此在此处需要DP。

如您的PDF所示，通过最小二乘法找到最佳拟合线条很简单，不需要DP。

块引用：

Opt（n） - e（i，n）+ C + Opt（i-1）---我们的成本函数，其中 C是新线段的恒定成本（如果没有它，问题就很简单，我们只需针对每两个点生成新的线段） e（i，n）是i到n点的一个线段（而不是递归的）的误差 Opt（i-1）是从第一点到（i-1）th的最小成本递归

现在是算法。

确保点列表按x值排序
M [0] = 0 --- 自我解释
对于所有i < j的对(i，j)：找到e（i，j）----（这将需要嵌套的for / foreach循环或类似结构的理解。将这些值存储在2D数组中！）
对于（j = 1..n）： M [j] = min（[Opt（j）for i in range（1，j）]）
所以基本上，找到任意两个可能点之间的单行成本，存储在e中
找到j为1到n之间的最小成本。一路上的值将有助于后续计算，因此请将它们存储起来！请注意，i也是Opt的参数。 M [n]是总优化成本。

你的问题是-如何确定分割发生的位置？您如何使用此功能和M来确定一旦全部结束就会出现线段集？

希望这可以帮助你！

- jon_darkstar