英译中:
计算OBB
可以使用PCA或者以下方法:
来获取3D OBB。链接中的代码需要转换成3D,但原理是相同的。这里有一个更高级的3D OBB逼近,使用了立方体映射的递归搜索(这里的代码和方法不如它)。
初始猜测
因此,OBB将给出定向边界框。其最大的一面将与您的圆柱体的旋转轴平行。因此,让我们从圆柱体外围绕绕着这个OBB开始。因此,中心轴将是OBB的中心,并且与其最大的一面平行。(如果没有最大的一面,则需要检查所有3种组合)。直径将是剩余面中的较大者。
拟合圆柱体
现在只需尝试囊括初始猜测附近所有点的“所有”偏移量和半径(也可能是高度),并记住最佳的一个(根据您想要的规格)。可以使用任何优化方法进行此操作,但我最喜欢的是这个:
结果的有效性取决于拟合过程。但是不要在嵌套拟合中变得过于复杂。
[编辑1] C++中的3D OBB
我很好奇,今天有些时间,所以我编码了类似于上面链接的2D示例的3D OBB。看起来它正在工作。这是预览:
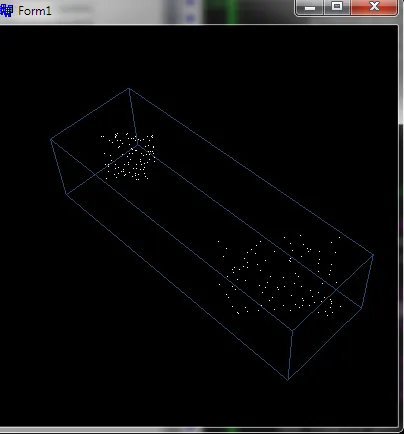
我用了2个聚类来验证方向... 这是代码(以简单的C++类形式):
class OBB3D
{
public:
double p0[3],u[3],v[3],w[3];
double V,l[3];
double p[8*3];
OBB3D() {}
OBB3D(OBB3D& a) { *this=a; }
~OBB3D() {}
OBB3D* operator = (const OBB3D *a) { *this=*a; return this; }
void compute(double *pnt,int num)
{
OBB3D o;
int i,j;
double a,_a,a0,a1,da,ca,sa; int ea;
double b,_b,b0,b1,db,cb,sb; int eb;
double c,_c,c0,c1,dc,cc,sc; int ec;
double u0[3],v0[3],pmin[3],pmax[3],q,*qq;
const double deg=M_PI/180.0;
p0[0]=0.0; u[0]=1.0; v[0]=0.0; w[0]=0.0; l[0]=0.0; V=-1.0;
p0[1]=0.0; u[1]=0.0; v[1]=1.0; w[1]=0.0; l[1]=0.0;
p0[2]=0.0; u[2]=0.0; v[2]=0.0; w[2]=1.0; l[2]=0.0;
if (num<3) { V=0.0; return; }
a0=0; a1=360.0*deg; da=10.0*deg; _a=a0;
b0=0; b1= 90.0*deg; db=10.0*deg; _b=b0;
c0=0; c1= 90.0*deg; dc=10.0*deg; _c=c0;
for (j=0;j<5;j++)
{
for (ea=1,a=a0;ea;a+=da){ if (a>=a1) { a=a1; ea=0; } ca=cos(a); sa=sin(a);
for (eb=1,b=b0;eb;b+=db){ if (b>=b1) { b=b1; eb=0; } cb=cos(b); sb=sin(b);
o.w[0]=cb*ca;
o.w[1]=cb*sa;
o.w[2]=sb;
vector_ld(u0,1.0,0.0,0.0);
if (fabs(vector_mul(u0,o.w))>0.75)
vector_ld(u0,0.0,1.0,0.0);
vector_mul(v0,o.w,u0);
vector_mul(u0,v0,o.w);
vector_one(u0,u0);
vector_one(v0,v0);
for (ec=1,c=c0;ec;c+=dc){ if (c>=c1) { c=c1; ec=0; } cc=cos(c); sc=sin(c);
for (i=0;i<3;i++)
{
o.u[i]=(u0[i]*cc)-(v0[i]*sc);
o.v[i]=(u0[i]*sc)+(v0[i]*cc);
}
pmin[0]=pmax[0]=vector_mul(pnt,o.u);
pmin[1]=pmax[1]=vector_mul(pnt,o.v);
pmin[2]=pmax[2]=vector_mul(pnt,o.w);
for (i=0;i<num;i+=3)
{
q=vector_mul(pnt+i,o.u); if (pmin[0]>q) pmin[0]=q; if (pmax[0]<q) pmax[0]=q;
q=vector_mul(pnt+i,o.v); if (pmin[1]>q) pmin[1]=q; if (pmax[1]<q) pmax[1]=q;
q=vector_mul(pnt+i,o.w); if (pmin[2]>q) pmin[2]=q; if (pmax[2]<q) pmax[2]=q;
}
for (o.V=1.0,i=0;i<3;i++) { o.l[i]=pmax[i]-pmin[i]; o.V*=o.l[i]; }
if ((V<0.0)||(V>o.V))
{
*this=o; _a=a; _b=b; _c=c;
for (i=0;i<3;i++) p0[i]=(pmin[0]*u[i])+(pmin[1]*v[i])+(pmin[2]*w[i]);
}
}
}}
a0=(_a-0.5*da); a1=a0+da; da*=0.1;
b0=(_b-0.5*db); b1=b0+db; db*=0.1;
c0=(_c-0.5*dc); c1=c0+dc; dc*=0.1;
}
{ i=0; qq=u; }
if (l[1]>l[i]){ i=1; qq=v; }
if (l[2]>l[i]){ i=2; qq=w; }
for (j=0;j<3;j++) { q=w[j]; w[j]=qq[j]; qq[j]=q; } q=l[2]; l[2]=l[i]; l[i]=q;
{ i=0; qq=u; }
if (l[1]>l[i]){ i=1; qq=v; }
for (j=0;j<3;j++) { q=v[j]; v[j]=qq[j]; qq[j]=q; } q=l[1]; l[1]=l[i]; l[i]=q;
for (i=0;i<3;i++)
{
j=i;
p[j]=p0[i] ; j+=3;
p[j]=p0[i]+(l[0]*u[i]) ; j+=3;
p[j]=p0[i]+(l[0]*u[i])+(l[1]*v[i]) ; j+=3;
p[j]=p0[i] +(l[1]*v[i]) ; j+=3;
p[j]=p0[i] +(l[2]*w[i]); j+=3;
p[j]=p0[i]+(l[0]*u[i]) +(l[2]*w[i]); j+=3;
p[j]=p0[i]+(l[0]*u[i])+(l[1]*v[i])+(l[2]*w[i]); j+=3;
p[j]=p0[i] +(l[1]*v[i])+(l[2]*w[i]); j+=3;
}
}
void gl_draw()
{
glBegin(GL_LINES);
glVertex3dv(p+ 0); glVertex3dv(p+ 3);
glVertex3dv(p+ 3); glVertex3dv(p+ 6);
glVertex3dv(p+ 6); glVertex3dv(p+ 9);
glVertex3dv(p+ 9); glVertex3dv(p+ 0);
glVertex3dv(p+12); glVertex3dv(p+15);
glVertex3dv(p+15); glVertex3dv(p+18);
glVertex3dv(p+18); glVertex3dv(p+21);
glVertex3dv(p+21); glVertex3dv(p+12);
glVertex3dv(p+ 0); glVertex3dv(p+12);
glVertex3dv(p+ 3); glVertex3dv(p+15);
glVertex3dv(p+ 6); glVertex3dv(p+18);
glVertex3dv(p+ 9); glVertex3dv(p+21);
glEnd();
}
} obb;
您只需使用点云数据调用计算函数,其中
num为点数的3倍。结果存储为单位基向量
u,v,w和原点
p0,以及每个轴的尺寸
l[]或
OBB的8个角点
p。
这个算法的实现非常简单,通过尝试所有球形位置(
w轴有一定的步长),然后尝试所有与
w垂直的
u,v极坐标位置,并记住最小体积的
OBB。然后递归搜索附近的最佳解决方案,以提高精度。
我认为这应该是一个不错的起点。如果您在循环
for (ec=1,c=c0;ec;c+=dc)中实现最小圆而不是
u,v旋转,则可以直接从此搜索中获得您的圆柱体。
代码还没有优化(例如
w轴检查等部分可以移动到嵌套的for循环的较低层),但我想尽可能保持它简单易懂。
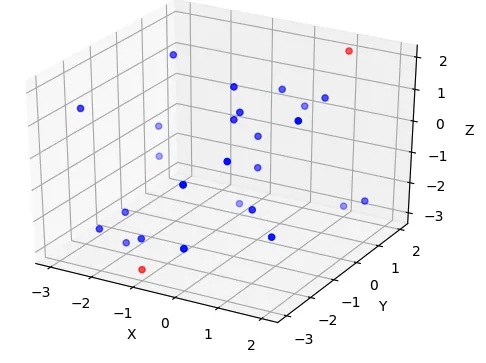
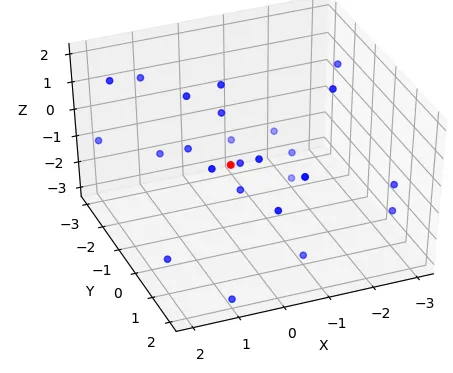
我成功地修改了我的3D OBB,通过用最小外接圆替换
U,V搜索(希望我实现得正确,但看起来是这样的...),找到所有投影在
UV平面上的点的最小外接2D圆,使其成为与
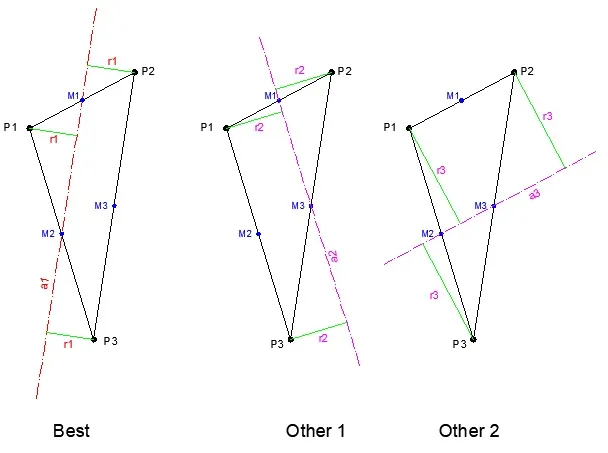
W平行的定向包围圆柱。我使用了
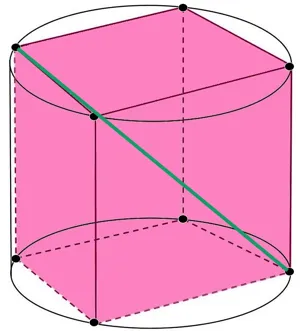
你提供的链接中的第一种方法(使用分界线)。以下是结果:

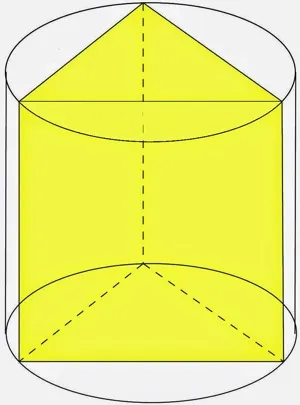
蓝色部分是
3D OBB,棕橙色部分是找到的
3D OBC。这是代码:
class OBC3D
{
public:
double p0[3],u[3],v[3],w[3];
double V,r,h;
double p1[3];
OBC3D() {}
OBC3D(OBC3D& a) { *this=a; }
~OBC3D() {}
OBC3D* operator = (const OBC3D *a) { *this=*a; return this; }
void compute(double *pnt,int num)
{
OBC3D o;
int i,j,k,kk,n;
double a,_a,a0,a1,da,ca,sa; int ea;
double b,_b,b0,b1,db,cb,sb; int eb;
double pmin[3],pmax[3],q,qq,*pnt2,p[3],c0,c1,u0,v0,du,dv,dr;
const double deg=M_PI/180.0;
p0[0]=0.0; u[0]=1.0; v[0]=0.0; w[0]=0.0; V=-1.0;
p0[1]=0.0; u[1]=0.0; v[1]=1.0; w[1]=0.0; r=0.0;
p0[2]=0.0; u[2]=0.0; v[2]=0.0; w[2]=1.0; h=0.0;
if (num<3) { V=0.0; return; }
pnt2=new double[num];
a0=0; a1=360.0*deg; da=10.0*deg; _a=a0;
b0=0; b1= 90.0*deg; db=10.0*deg; _b=b0;
for (k=0;k<5;k++)
{
for (ea=1,a=a0;ea;a+=da){ if (a>=a1) { a=a1; ea=0; } ca=cos(a); sa=sin(a);
for (eb=1,b=b0;eb;b+=db){ if (b>=b1) { b=b1; eb=0; } cb=cos(b); sb=sin(b);
o.w[0]=cb*ca;
o.w[1]=cb*sa;
o.w[2]=sb;
vector_ld(o.u,1.0,0.0,0.0);
if (fabs(vector_mul(o.u,o.w))>0.75)
vector_ld(o.u,0.0,1.0,0.0);
vector_mul(o.v,o.w,o.u);
vector_mul(o.u,o.v,o.w);
vector_one(o.u,o.u);
vector_one(o.v,o.v);
pmin[0]=pmax[0]=vector_mul(pnt,o.u);
pmin[1]=pmax[1]=vector_mul(pnt,o.v);
pmin[2]=pmax[2]=vector_mul(pnt,o.w);
for (i=0;i<num;i+=3)
{
q=vector_mul(pnt+i,o.u); if (pmin[0]>q) pmin[0]=q; if (pmax[0]<q) pmax[0]=q; pnt2[i+0]=q;
q=vector_mul(pnt+i,o.v); if (pmin[1]>q) pmin[1]=q; if (pmax[1]<q) pmax[1]=q; pnt2[i+1]=q;
q=vector_mul(pnt+i,o.w); if (pmin[2]>q) pmin[2]=q; if (pmax[2]<q) pmax[2]=q; pnt2[i+2]=q;
}
n=0;
for (u0=0.0,v0=0.0,i=0;i<num;i+=3)
{
u0+=pnt2[i+0];
v0+=pnt2[i+1];
} q=3.0/double(num); u0*=q; v0*=q;
for (o.r=0.0,i=0;i<num;i+=3)
{
c0=pnt2[i+0]-u0;
c1=pnt2[i+1]-v0;
q=(c0*c0)+(c1*c1);
if (o.r<q) o.r=q;
} o.r=sqrt(o.r);
for (kk=0;kk<4;kk++)
{
qq=o.r*o.r;
for (i=n;i<num;i+=3)
{
c0=pnt2[i+0]-u0;
c1=pnt2[i+1]-v0;
q=fabs((c0*c0)+(c1*c1)-qq);
if (q<1e-10)
{
pnt2[n+0]=pnt2[i+0];
pnt2[n+1]=pnt2[i+1];
pnt2[n+2]=pnt2[i+2]; n+=3;
}
}
for (du=0.0,dv=0.0,i=0;i<n;i+=3)
{
du+=pnt2[i+0]-u0;
dv+=pnt2[i+1]-v0;
} q=1.0/sqrt((du*du)+(dv*dv)); du*=q; dv*=q;
for (dr=0.1*o.r,j=0;j<5;)
{
u0+=dr*du;
v0+=dr*dv;
for (qq=0.0,i=0;i<num;i+=3)
{
c0=pnt2[i+0]-u0;
c1=pnt2[i+1]-v0;
q=(c0*c0)+(c1*c1);
if (qq<q) qq=q;
} qq=sqrt(qq);
if (qq>o.r)
{
u0-=dr*du;
v0-=dr*dv;
dr*=0.1;
j++;
}
else o.r=qq;
}
}
o.h=pmax[2]-pmin[2];
o.V=M_PI*o.r*o.r*o.h;
if ((V<0.0)||(V>o.V))
{
*this=o; _a=a; _b=b;
for (i=0;i<3;i++) p0[i]=(u0*u[i])+(v0*v[i])+(pmin[2]*w[i]);
}
}}
a0=(_a-0.5*da); a1=a0+da; da*=0.1;
b0=(_b-0.5*db); b1=b0+db; db*=0.1;
}
for (i=0;i<3;i++) p1[i]=p0[i]+(h*w[i]);
delete[] pnt2;
}
void gl_draw()
{
int i,j,n=36;
double a,da=2.0*M_PI/double(n),p[3],uu,vv;
glBegin(GL_LINES);
glVertex3dv(p0); glVertex3dv(p1);
glEnd();
glBegin(GL_LINE_LOOP);
for (a=0.0,i=0;i<n;i++,a+=da)
{
uu=r*cos(a);
vv=r*sin(a);
for (j=0;j<3;j++) p[j]=p0[j]+(u[j]*uu)+(v[j]*vv);
glVertex3dv(p);
}
glEnd();
glBegin(GL_LINE_LOOP);
for (a=0.0,i=0;i<n;i++,a+=da)
{
uu=r*cos(a);
vv=r*sin(a);
for (j=0;j<3;j++) p[j]=p1[j]+(u[j]*uu)+(v[j]*vv);
glVertex3dv(p);
}
glEnd();
}
};
使用方法相同...我用这个进行了测试:
OBB3D obb;
OBC3D obc;
void compute()
{
int i,n=500;
Randomize();
RandSeed=98123456789;
pnt.allocate(3*n); pnt.num=0;
double u[3],v[3],w[3],x,y,z,a;
for (i=0;i<3;i++) w[i]=Random()-0.5;
vector_one(w,w);
vector_ld(u,1.0,0.0,0.0);
if (fabs(vector_mul(u,w))>0.75)
vector_ld(u,0.0,1.0,0.0);
vector_mul(v,w,u);
vector_mul(u,v,w);
vector_one(u,u);
vector_one(v,v);
for (i=0;i<n;i++)
{
a=2.0*M_PI*Random();
x= 0.5+(0.75*(Random()-0.5))*cos(a);
y=-0.3+(0.50*(Random()-0.5))*sin(a);
z= 0.4+(0.90*(Random()-0.5));
pnt.add((x*u[0])+(y*v[0])+(z*w[0]));
pnt.add((x*u[1])+(y*v[1])+(z*w[1]));
pnt.add((x*u[2])+(y*v[2])+(z*w[2]));
}
obb.compute(pnt.dat,pnt.num);
obc.compute(pnt.dat,pnt.num);
}
这里的 List<double> pnt 是我的动态数组模板 double pnt[],但这并不重要。
请注意,如果您选择了过大的初始步长(da,db)进行 W 方向搜索,可能会陷入局部最小值而错过正确的解。
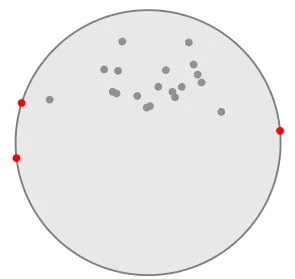
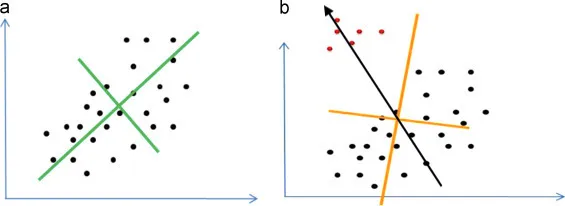


x,y要拟合,这应该不难。你有样本数据集吗? - Spektre