如何在高维超球面表面均匀分布点？

Question

我希望能够在三维及以上的球面上均匀分布N个点。

具体要求如下：

• 给定点数N和维度D（其中D > 1，N > 1）
• 每个点到原点的距离必须为1
• 任何两个点之间的最小距离应尽可能大
• 每个点到其最近邻的距离不一定相同（事实上，除非点数形成一个立方体的顶点或者N <= D，否则不可能是相同的）。

我不感兴趣的是：

• 在超球面上创建均匀随机分布，因为我想让任意两个点之间的最小距离尽可能大，而不是随机分布。
• 粒子斥力模拟类型的方法，因为它们很难实现，并且对于较大的N运行时间非常长（理想情况下，该方法应具有确定性并且O(n)）。

满足这些条件的一种方法称为斐波那契格点法，但我只能找到2d和3d的代码实现。

斐波那契格点法（也称为斐波那契螺旋）的方法是生成一个1d线，该线在球面上螺旋，以便每个转弯处覆盖的表面积大致相同。然后，您可以在螺旋线上均匀放置N个点，它们将大致均匀地分布在球面上。

这个答案中有一个针对三维空间的Python实现，可以生成以下内容：

我想知道斐波那契螺旋是否可以扩展到高于3维，并在数学堆栈交换上发布了一个问题。令我惊讶的是，我收到了两个惊人的答案，据我所知（因为我不完全理解所示的数学），它确实可以将此方法扩展到N维。

不幸的是，我不理解所示数学的足够多，无法将任何一个答案转化为（伪）代码。我是一名经验丰富的计算机程序员，但我的数学背景只有那么多。

我将复制下面其中一个答案中我认为最重要的部分（不幸的是SO不支持mathjax，所以我必须复制为图像）。

我遇到的困难:

• 如何解决用于ψn的反函数?
• 给出的示例是d = 3。如何为任意d生成公式?

这里是否有了解涉及数学的人能够实现链接的斐波那契晶格问题的伪代码实现？我知道完整的实现可能相当困难，所以如果能够部分实现并带领我完成其余部分，我会很高兴。

为了使它更容易，我已经编写了一个函数，将N维球面坐标转换为笛卡尔坐标，因此实现可以输出其中之一，因为我可以轻松转换。

此外，我看到一个答案使用下一个质数来表示每个附加维度。我可以轻松编写一个函数，输出每个连续的质数，因此您可以假设已经实现。

如果不能在N维中实现斐波那契晶格，则我愿意接受满足上述约束条件的其他方法。

- F Chopin

---

我理解这个问题本质上是“将其他答案中的方程转换为伪代码”。希望这是适合在这里询问的问题类型，但如果不是，请告诉我。此外，如果我应该从那个答案中复制任何信息到这个问题中，以使它不再是一个“仅链接”类型的问题，请让我知道。 - F Chopin

我很乐意提供帮助，并且我有很高的可能性能够做到，但如果你定义了什么是斐波那契格点阵，那么这将大大简化工作量。我知道斐波那契是谁以及什么是格点阵，但我不知道什么是斐波那契格点阵。 - Lajos Arpad

Karl，当我使用“解决方案”这个术语时，我当然是指符合标准的解决方案，也就是任意两点之间的最小距离是最大的。 - Lajos Arpad

@LajosArpad，谢谢你，我已经更新了我的问题，加入了我们在此讨论过的定义。 - F Chopin

@Karl 顺便说一下，我刚刚发现了这个很棒的答案 uniform points on sphere using Gaussian distribution PRNG，它与我的新答案几乎相同（除了它使用 PRNG 而不是像我一样直接生成分布）。也许通过结合这两种方法，结果会更精确...而且这很容易在任何维度上移植，无需更改常数或方程式。 - Spektre

Answer 1

非常有趣的问题。我想把它实现到我的4D渲染引擎中，因为我很好奇它会是什么样子，但我太懒了，也没有能力从数学上解决ND超越问题。

相反，我提出了不同的解决方案。这不是一个斐波那契栅格 !!! 相反，我将超球或n-球的参数方程扩展成超螺旋，然后只需调整螺旋参数，使点更或多或少地等距分布。

我知道这听起来很糟糕，但并不难，而且结果看起来对我来说是正确的（最终解决了一些愚蠢的拼写错误/复制粘贴错误）

主要思路是使用n维参数方程计算超球的表面点，从角度和半径计算。这里是实现：

• 算法来栅格化和填充超球？

请参见[编辑2]。现在问题归结为两个主要问题：

1. compute number of screws

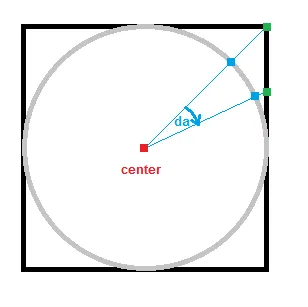
   so if we want that our points are equidistant so they must lye on the spiral path in equidistances (see bullet #2) but also the screws itself should have the same distance between each other. For that we can exploit geometrical properties of the hypersphere. Let start with 2D:

   

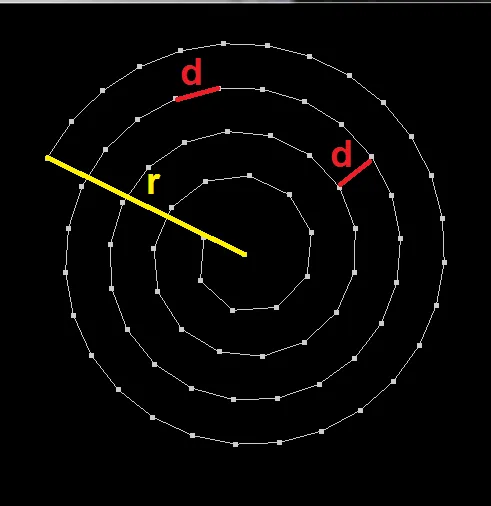
   so simply screws = r/d. The number of points can be also inferred as points = area/d^2 = PI*r^2/d^2.

   so we can simply write 2D spiral as:

   t = <0.0,1.0>
   a = 2.0*M_PI*screws*t;
   x = r*t*cos(a);
   y = r*t*sin(a);
   

   To be more simple we can assume r=1.0 so d=d/r (and just scale the points later). Then the expansions (each dimension just adds angle parameter) look like this:

   2D:

   screws=1.0/d;          // radius/d
   points=M_PI/(d*d);     // surface_area/d^2
   a = 2.0*M_PI*t*screws;
   x = t*cos(a);
   y = t*sin(a);
   

   3D:

   screws=M_PI/d;         // half_circumference/d
   points=4.0*M_PI/(d*d); // surface_area/d^2
   a=    M_PI*t;
   b=2.0*M_PI*t*screws;
   x=cos(a)       ;
   y=sin(a)*cos(b);
   z=sin(a)*sin(b);
   

   4D:

   screws = M_PI/d;
   points = 3.0*M_PI*M_PI*M_PI/(4.0*d*d*d);
   a=    M_PI*t;
   b=    M_PI*t*screws;
   c=2.0*M_PI*t*screws*screws;
   x=cos(a)              ;
   y=sin(a)*cos(b)       ;
   z=sin(a)*sin(b)*cos(c);
   w=sin(a)*sin(b)*sin(c);
   

   Now beware points for 4D are just my assumption. I empirically found out that they relate to constant/d^3 but not exactly. The screws are different for each angle. Mine assumption is that there is no other scale than screws^i but it might need some constant tweaking (did not do analysis of the resulting point-cloud as the result look ok to me)

   Now we can generate any point on spiral from single parameter t=<0.0,1.0>.

   Note if you reverse the equation so d=f(points) you can have points as input value but beware its just approximate number of points not exact !!!

2. generate step on spirals so points are equidistant

   This is the part I skip the algebraic mess and use fitting instead. I simply binary search delta t so the resulting point is d distant to previous point. So simply generate point t=0 and then binary search t near estimated position until is d distant to the start point. Then repeat this until t<=1.0 ...

   You can use binary search or what ever. I know its not as fast as O(1) algebraic approach but no need to derive the stuff for each dimension... Looks 10 iterations are enough for fitting so its not that slow either.

这是我使用C++/GL/VCL实现的4D引擎：

void ND_mesh::set_HyperSpiral(int N,double r,double d)
    {
    int i,j;
    reset(N);
    d/=r;   // unit hyper-sphere
    double dd=d*d;  // d^2
    if (n==2)
        {
        // r=1,d=!,screws=?
        // S = PI*r^2
        // screws = r/d
        // points = S/d^2
        int i0,i;
        double a,da,t,dt,dtt;
        double x,y,x0,y0;
        double screws=1.0/d;
        double points=M_PI/(d*d);
        dbg=points;
        da=2.0*M_PI*screws;
        x0=0.0; pnt.add(x0);
        y0=0.0; pnt.add(y0);
        dt=0.1*(1.0/points);
        for (t=0.0,i0=0,i=1;;i0=i,i++)
            {
            for (dtt=dt,j=0;j<10;j++,dtt*=0.5)
                {
                t+=dtt;
                a=da*t;
                x=(t*cos(a))-x0; x*=x;
                y=(t*sin(a))-y0; y*=y;
                if ((!j)&&(x+y<dd)){ j--; t-=dtt; dtt*=4.0; continue; }
                if (x+y>dd) t-=dtt;
                }
            if (t>1.0) break;
            a=da*t;
            x0=t*cos(a); pnt.add(x0);
            y0=t*sin(a); pnt.add(y0);
            as2(i0,i);
            }
        }
    if (n==3)
        {
        // r=1,d=!,screws=?
        // S = 4*PI*r^2
        // screws = 2*PI*r/(2*d)
        // points = S/d^2
        int i0,i;
        double a,b,da,db,t,dt,dtt;
        double x,y,z,x0,y0,z0;
        double screws=M_PI/d;
        double points=4.0*M_PI/(d*d);
        dbg=points;
        da=    M_PI;
        db=2.0*M_PI*screws;
        x0=1.0; pnt.add(x0);
        y0=0.0; pnt.add(y0);
        z0=0.0; pnt.add(z0);
        dt=0.1*(1.0/points);
        for (t=0.0,i0=0,i=1;;i0=i,i++)
            {
            for (dtt=dt,j=0;j<10;j++,dtt*=0.5)
                {
                t+=dtt;
                a=da*t;
                b=db*t;
                x=cos(a)       -x0; x*=x;
                y=sin(a)*cos(b)-y0; y*=y;
                z=sin(a)*sin(b)-z0; z*=z;
                if ((!j)&&(x+y+z<dd)){ j--; t-=dtt; dtt*=4.0; continue; }
                if (x+y+z>dd) t-=dtt;
                }
            if (t>1.0) break;
            a=da*t;
            b=db*t;
            x0=cos(a)       ; pnt.add(x0);
            y0=sin(a)*cos(b); pnt.add(y0);
            z0=sin(a)*sin(b); pnt.add(z0);
            as2(i0,i);
            }
        }
    if (n==4)
        {
        // r=1,d=!,screws=?
        // S = 2*PI^2*r^3
        // screws = 2*PI*r/(2*d)
        // points = 3*PI^3/(4*d^3);
        int i0,i;
        double a,b,c,da,db,dc,t,dt,dtt;
        double x,y,z,w,x0,y0,z0,w0;
        double screws = M_PI/d;
        double points=3.0*M_PI*M_PI*M_PI/(4.0*d*d*d);
        dbg=points;
        da=    M_PI;
        db=    M_PI*screws;
        dc=2.0*M_PI*screws*screws;
        x0=1.0; pnt.add(x0);
        y0=0.0; pnt.add(y0);
        z0=0.0; pnt.add(z0);
        w0=0.0; pnt.add(w0);
        dt=0.1*(1.0/points);
        for (t=0.0,i0=0,i=1;;i0=i,i++)
            {
            for (dtt=dt,j=0;j<10;j++,dtt*=0.5)
                {
                t+=dtt;
                a=da*t;
                b=db*t;
                c=dc*t;
                x=cos(a)              -x0; x*=x;
                y=sin(a)*cos(b)       -y0; y*=y;
                z=sin(a)*sin(b)*cos(c)-z0; z*=z;
                w=sin(a)*sin(b)*sin(c)-w0; w*=w;
                if ((!j)&&(x+y+z+w<dd)){ j--; t-=dtt; dtt*=4.0; continue; }
                if (x+y+z+w>dd) t-=dtt;
                } dt=dtt;
            if (t>1.0) break;
            a=da*t;
            b=db*t;
            c=dc*t;
            x0=cos(a)              ; pnt.add(x0);
            y0=sin(a)*cos(b)       ; pnt.add(y0);
            z0=sin(a)*sin(b)*cos(c); pnt.add(z0);
            w0=sin(a)*sin(b)*sin(c); pnt.add(w0);
            as2(i0,i);
            }
        }

    for (i=0;i<pnt.num;i++) pnt.dat[i]*=r;
    for (i=0;i<s1.num;i++) s1.dat[i]*=n;
    for (i=0;i<s2.num;i++) s2.dat[i]*=n;
    for (i=0;i<s3.num;i++) s3.dat[i]*=n;
    for (i=0;i<s4.num;i++) s4.dat[i]*=n;
    }

在这里，“n=N”表示设置维度，“r”表示半径，“d”表示点之间的期望距离。我使用了很多未在此处声明的内容，但重要的是，“pnt []”列出了对象上的点列表，“as2（i0，i1）”将从索引“i0，i1”处的点添加到网格中的线。

以下是一些屏幕截图...

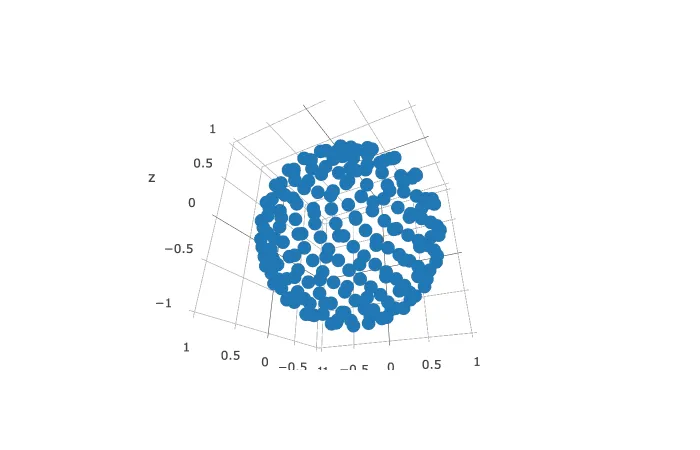
3D透视图：

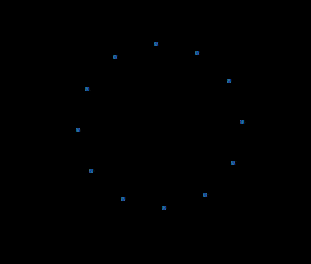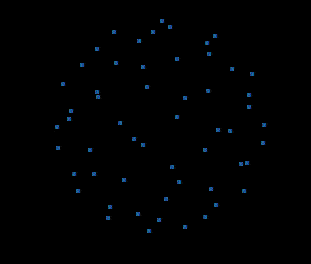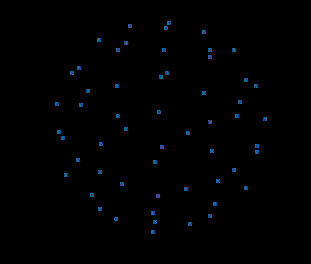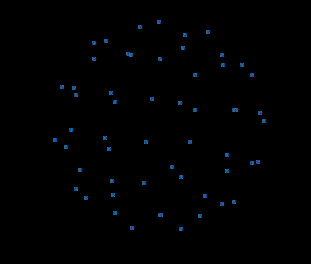
4D视角：

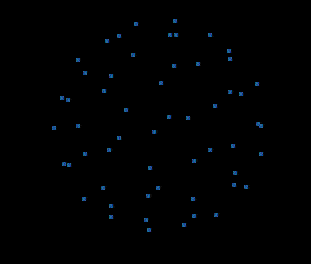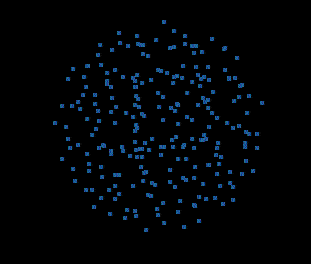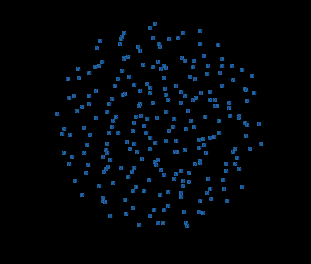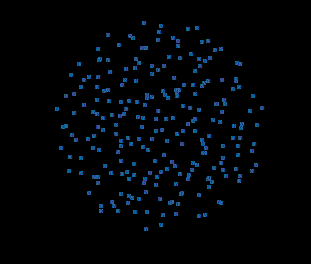
超平面w=0.0的4D截面：

并且同样具有更多的点和更大的半径：

形状随着旋转而变化，其中包括其动画...

[编辑1] 更多代码/信息

这是我的引擎网格类的样子：

//---------------------------------------------------------------------------
//--- ND Mesh: ver 1.001 ----------------------------------------------------
//---------------------------------------------------------------------------
#ifndef _ND_mesh_h
#define _ND_mesh_h
//---------------------------------------------------------------------------
#include "list.h"     // my dynamic list you can use std::vector<> instead
#include "nd_reper.h" // this is just 5x5 transform matrix
//---------------------------------------------------------------------------
enum _render_enum
    {
    _render_Wireframe=0,
    _render_Polygon,
    _render_enums
    };
const AnsiString _render_txt[]=
    {
    "Wireframe",
    "Polygon"
    };
enum _view_enum
    {
    _view_Orthographic=0,
    _view_Perspective,
    _view_CrossSection,
    _view_enums
    };
const AnsiString _view_txt[]=
    {
    "Orthographic",
    "Perspective",
    "Cross section"
    };
struct dim_reduction
    {
    int view;               // _view_enum
    double coordinate;      // cross section hyperplane coordinate or camera focal point looking in W+ direction
    double focal_length;
    dim_reduction()     { view=_view_Perspective; coordinate=-3.5; focal_length=2.0; }
    dim_reduction(dim_reduction& a) { *this=a; }
    ~dim_reduction()    {}
    dim_reduction* operator = (const dim_reduction *a) { *this=*a; return this; }
    //dim_reduction* operator = (const dim_reduction &a) { ...copy... return this; }
    };
//---------------------------------------------------------------------------
class ND_mesh
    {
public:
    int n;              // dimensions

    List<double> pnt;   // ND points        (x0,x1,x2,x3,...x(n-1))
    List<int>    s1;    // ND points        (i0)
    List<int>    s2;    // ND wireframe     (i0,i1)
    List<int>    s3;    // ND triangles     (i0,i1,i2,)
    List<int>    s4;    // ND tetrahedrons  (i0,i1,i2,i3)
    DWORD col;          // object color 0x00BBGGRR
    int   dbg;          // debug/test variable

    ND_mesh()   { reset(0); }
    ND_mesh(ND_mesh& a) { *this=a; }
    ~ND_mesh()  {}
    ND_mesh* operator = (const ND_mesh *a) { *this=*a; return this; }
    //ND_mesh* operator = (const ND_mesh &a) { ...copy... return this; }

    // add simplex
    void as1(int a0)                     { s1.add(a0); }
    void as2(int a0,int a1)              { s2.add(a0); s2.add(a1); }
    void as3(int a0,int a1,int a2)       { s3.add(a0); s3.add(a1); s3.add(a2); }
    void as4(int a0,int a1,int a2,int a3){ s4.add(a0); s4.add(a1); s4.add(a2); s4.add(a3); }
    // init ND mesh
    void reset(int N);
    void set_HyperTetrahedron(int N,double a);              // dimensions, side
    void set_HyperCube       (int N,double a);              // dimensions, side
    void set_HyperSphere     (int N,double r,int points);   // dimensions, radius, points per axis
    void set_HyperSpiral     (int N,double r,double d);     // dimensions, radius, distance between points
    // render
    void glDraw(ND_reper &rep,dim_reduction *cfg,int render);   // render mesh
    };
//---------------------------------------------------------------------------
#define _cube(a0,a1,a2,a3,a4,a5,a6,a7) { as4(a1,a2,a4,a7); as4(a0,a1,a2,a4); as4(a2,a4,a6,a7); as4(a1,a2,a3,a7); as4(a1,a4,a5,a7); }
//---------------------------------------------------------------------------
void ND_mesh::reset(int N)
    {
    dbg=0;
    if (N>=0) n=N;
    pnt.num=0;
    s1.num=0;
    s2.num=0;
    s3.num=0;
    s4.num=0;
    col=0x00AAAAAA;
    }
//---------------------------------------------------------------------------
void ND_mesh::set_HyperSpiral(int N,double r,double d)
    {
    int i,j;
    reset(N);
    d/=r;   // unit hyper-sphere
    double dd=d*d;  // d^2
    if (n==2)
        {
        // r=1,d=!,screws=?
        // S = PI*r^2
        // screws = r/d
        // points = S/d^2
        int i0,i;
        double a,da,t,dt,dtt;
        double x,y,x0,y0;
        double screws=1.0/d;
        double points=M_PI/(d*d);
        dbg=points;
        da=2.0*M_PI*screws;
        x0=0.0; pnt.add(x0);
        y0=0.0; pnt.add(y0);
        dt=0.1*(1.0/points);
        for (t=0.0,i0=0,i=1;;i0=i,i++)
            {
            for (dtt=dt,j=0;j<10;j++,dtt*=0.5)
                {
                t+=dtt;
                a=da*t;
                x=(t*cos(a))-x0; x*=x;
                y=(t*sin(a))-y0; y*=y;
                if ((!j)&&(x+y<dd)){ j--; t-=dtt; dtt*=4.0; continue; }
                if (x+y>dd) t-=dtt;
                }
            if (t>1.0) break;
            a=da*t;
            x0=t*cos(a); pnt.add(x0);
            y0=t*sin(a); pnt.add(y0);
            as2(i0,i);
            }
        }
    if (n==3)
        {
        // r=1,d=!,screws=?
        // S = 4*PI*r^2
        // screws = 2*PI*r/(2*d)
        // points = S/d^2
        int i0,i;
        double a,b,da,db,t,dt,dtt;
        double x,y,z,x0,y0,z0;
        double screws=M_PI/d;
        double points=4.0*M_PI/(d*d);
        dbg=points;
        da=    M_PI;
        db=2.0*M_PI*screws;
        x0=1.0; pnt.add(x0);
        y0=0.0; pnt.add(y0);
        z0=0.0; pnt.add(z0);
        dt=0.1*(1.0/points);
        for (t=0.0,i0=0,i=1;;i0=i,i++)
            {
            for (dtt=dt,j=0;j<10;j++,dtt*=0.5)
                {
                t+=dtt;
                a=da*t;
                b=db*t;
                x=cos(a)       -x0; x*=x;
                y=sin(a)*cos(b)-y0; y*=y;
                z=sin(a)*sin(b)-z0; z*=z;
                if ((!j)&&(x+y+z<dd)){ j--; t-=dtt; dtt*=4.0; continue; }
                if (x+y+z>dd) t-=dtt;
                }
            if (t>1.0) break;
            a=da*t;
            b=db*t;
            x0=cos(a)       ; pnt.add(x0);
            y0=sin(a)*cos(b); pnt.add(y0);
            z0=sin(a)*sin(b); pnt.add(z0);
            as2(i0,i);
            }
        }
    if (n==4)
        {
        // r=1,d=!,screws=?
        // S = 2*PI^2*r^3
        // screws = 2*PI*r/(2*d)
        // points = 3*PI^3/(4*d^3);
        int i0,i;
        double a,b,c,da,db,dc,t,dt,dtt;
        double x,y,z,w,x0,y0,z0,w0;
        double screws = M_PI/d;
        double points=3.0*M_PI*M_PI*M_PI/(4.0*d*d*d);
        dbg=points;
        da=    M_PI;
        db=    M_PI*screws;
        dc=2.0*M_PI*screws*screws;
        x0=1.0; pnt.add(x0);
        y0=0.0; pnt.add(y0);
        z0=0.0; pnt.add(z0);
        w0=0.0; pnt.add(w0);
        dt=0.1*(1.0/points);
        for (t=0.0,i0=0,i=1;;i0=i,i++)
            {
            for (dtt=dt,j=0;j<10;j++,dtt*=0.5)
                {
                t+=dtt;
                a=da*t;
                b=db*t;
                c=dc*t;
                x=cos(a)              -x0; x*=x;
                y=sin(a)*cos(b)       -y0; y*=y;
                z=sin(a)*sin(b)*cos(c)-z0; z*=z;
                w=sin(a)*sin(b)*sin(c)-w0; w*=w;
                if ((!j)&&(x+y+z+w<dd)){ j--; t-=dtt; dtt*=4.0; continue; }
                if (x+y+z+w>dd) t-=dtt;
                } dt=dtt;
            if (t>1.0) break;
            a=da*t;
            b=db*t;
            c=dc*t;
            x0=cos(a)              ; pnt.add(x0);
            y0=sin(a)*cos(b)       ; pnt.add(y0);
            z0=sin(a)*sin(b)*cos(c); pnt.add(z0);
            w0=sin(a)*sin(b)*sin(c); pnt.add(w0);
            as2(i0,i);
            }
        }

    for (i=0;i<pnt.num;i++) pnt.dat[i]*=r;
    for (i=0;i<s1.num;i++) s1.dat[i]*=n;
    for (i=0;i<s2.num;i++) s2.dat[i]*=n;
    for (i=0;i<s3.num;i++) s3.dat[i]*=n;
    for (i=0;i<s4.num;i++) s4.dat[i]*=n;
    }
//---------------------------------------------------------------------------
void ND_mesh::glDraw(ND_reper &rep,dim_reduction *cfg,int render)
    {
    int N,i,j,i0,i1,i2,i3;
    const int n0=0,n1=n,n2=n+n,n3=n2+n,n4=n3+n;
    double a,b,w,F,*p0,*p1,*p2,*p3,_zero=1e-6;
    vector<4> v;
    List<double> tmp,t0;        // temp
    List<double> S1,S2,S3,S4;   // reduced simplexes
    #define _swap(aa,bb) { double *p=aa.dat; aa.dat=bb.dat; bb.dat=p; int q=aa.siz; aa.siz=bb.siz; bb.siz=q; q=aa.num; aa.num=bb.num; bb.num=q; }

    // apply transform matrix pnt -> tmp
    tmp.allocate(pnt.num); tmp.num=pnt.num;
    for (i=0;i<pnt.num;i+=n)
        {
        v.ld(0.0,0.0,0.0,0.0);
        for (j=0;j<n;j++) v.a[j]=pnt.dat[i+j];
        rep.l2g(v,v);
        for (j=0;j<n;j++) tmp.dat[i+j]=v.a[j];
        }
    // copy simplexes and convert point indexes to points (only due to cross section)
    S1.allocate(s1.num*n); S1.num=0; for (i=0;i<s1.num;i++) for (j=0;j<n;j++) S1.add(tmp.dat[s1.dat[i]+j]);
    S2.allocate(s2.num*n); S2.num=0; for (i=0;i<s2.num;i++) for (j=0;j<n;j++) S2.add(tmp.dat[s2.dat[i]+j]);
    S3.allocate(s3.num*n); S3.num=0; for (i=0;i<s3.num;i++) for (j=0;j<n;j++) S3.add(tmp.dat[s3.dat[i]+j]);
    S4.allocate(s4.num*n); S4.num=0; for (i=0;i<s4.num;i++) for (j=0;j<n;j++) S4.add(tmp.dat[s4.dat[i]+j]);

    // reduce dimensions
    for (N=n;N>2;)
        {
        N--;
        if (cfg[N].view==_view_Orthographic){}  // no change
        if (cfg[N].view==_view_Perspective)
            {
            w=cfg[N].coordinate;
            F=cfg[N].focal_length;
            for (i=0;i<S1.num;i+=n)
                {
                a=S1.dat[i+N]-w;
                if (a>=F) a=F/a; else a=0.0;
                for (j=0;j<n;j++) S1.dat[i+j]*=a;
                }
            for (i=0;i<S2.num;i+=n)
                {
                a=S2.dat[i+N]-w;
                if (a>=F) a=F/a; else a=0.0;
                for (j=0;j<n;j++) S2.dat[i+j]*=a;
                }
            for (i=0;i<S3.num;i+=n)
                {
                a=S3.dat[i+N]-w;
                if (a>=F) a=F/a; else a=0.0;
                for (j=0;j<n;j++) S3.dat[i+j]*=a;
                }
            for (i=0;i<S4.num;i+=n)
                {
                a=S4.dat[i+N]-w;
                if (a>=F) a=F/a; else a=0.0;
                for (j=0;j<n;j++) S4.dat[i+j]*=a;
                }
            }
        if (cfg[N].view==_view_CrossSection)
            {
            w=cfg[N].coordinate;
            _swap(S1,tmp); for (S1.num=0,i=0;i<tmp.num;i+=n1)               // points
                {
                p0=tmp.dat+i+n0;
                if (fabs(p0[N]-w)<=_zero)
                    {
                    for (j=0;j<n;j++) S1.add(p0[j]);
                    }
                }
            _swap(S2,tmp); for (S2.num=0,i=0;i<tmp.num;i+=n2)               // lines
                {
                p0=tmp.dat+i+n0;              a=p0[N];              b=p0[N];// a=min,b=max
                p1=tmp.dat+i+n1; if (a>p1[N]) a=p1[N]; if (b<p1[N]) b=p1[N];
                if (fabs(a-w)+fabs(b-w)<=_zero)                             // fully inside
                    {
                    for (j=0;j<n;j++) S2.add(p0[j]);
                    for (j=0;j<n;j++) S2.add(p1[j]);
                    continue;
                    }
                if ((a<=w)&&(b>=w))                                         // intersection -> points
                    {
                    a=(w-p0[N])/(p1[N]-p0[N]);
                    for (j=0;j<n;j++) S1.add(p0[j]+a*(p1[j]-p0[j]));
                    }
                }
            _swap(S3,tmp); for (S3.num=0,i=0;i<tmp.num;i+=n3)               // triangles
                {
                p0=tmp.dat+i+n0;              a=p0[N];              b=p0[N];// a=min,b=max
                p1=tmp.dat+i+n1; if (a>p1[N]) a=p1[N]; if (b<p1[N]) b=p1[N];
                p2=tmp.dat+i+n2; if (a>p2[N]) a=p2[N]; if (b<p2[N]) b=p2[N];
                if (fabs(a-w)+fabs(b-w)<=_zero)                             // fully inside
                    {
                    for (j=0;j<n;j++) S3.add(p0[j]);
                    for (j=0;j<n;j++) S3.add(p1[j]);
                    for (j=0;j<n;j++) S3.add(p2[j]);
                    continue;
                    }
                if ((a<=w)&&(b>=w))                                         // cross section -> t0
                    {
                    t0.num=0;
                    i0=0; if (p0[N]<w-_zero) i0=1; if (p0[N]>w+_zero) i0=2;
                    i1=0; if (p1[N]<w-_zero) i1=1; if (p1[N]>w+_zero) i1=2;
                    i2=0; if (p2[N]<w-_zero) i2=1; if (p2[N]>w+_zero) i2=2;
                    if (i0+i1==3){ a=(w-p0[N])/(p1[N]-p0[N]); for (j=0;j<n;j++) t0.add(p0[j]+a*(p1[j]-p0[j])); }
                    if (i1+i2==3){ a=(w-p1[N])/(p2[N]-p1[N]); for (j=0;j<n;j++) t0.add(p1[j]+a*(p2[j]-p1[j])); }
                    if (i2+i0==3){ a=(w-p2[N])/(p0[N]-p2[N]); for (j=0;j<n;j++) t0.add(p2[j]+a*(p0[j]-p2[j])); }
                    if (!i0) for (j=0;j<n;j++) t0.add(p0[j]);
                    if (!i1) for (j=0;j<n;j++) t0.add(p1[j]);
                    if (!i2) for (j=0;j<n;j++) t0.add(p2[j]);
                    if (t0.num==n1) for (j=0;j<t0.num;j++) S1.add(t0.dat[j]);// copy t0 to target simplex based on points count
                    if (t0.num==n2) for (j=0;j<t0.num;j++) S2.add(t0.dat[j]);
                    if (t0.num==n3) for (j=0;j<t0.num;j++) S3.add(t0.dat[j]);
                    }
                }
            _swap(S4,tmp); for (S4.num=0,i=0;i<tmp.num;i+=n4)               // tetrahedrons
                {
                p0=tmp.dat+i+n0;              a=p0[N];              b=p0[N];// a=min,b=max
                p1=tmp.dat+i+n1; if (a>p1[N]) a=p1[N]; if (b<p1[N]) b=p1[N];
                p2=tmp.dat+i+n2; if (a>p2[N]) a=p2[N]; if (b<p2[N]) b=p2[N];
                p3=tmp.dat+i+n3; if (a>p3[N]) a=p3[N]; if (b<p3[N]) b=p3[N];
                if (fabs(a-w)+fabs(b-w)<=_zero)                             // fully inside
                    {
                    for (j=0;j<n;j++) S4.add(p0[j]);
                    for (j=0;j<n;j++) S4.add(p1[j]);
                    for (j=0;j<n;j++) S4.add(p2[j]);
                    for (j=0;j<n;j++) S4.add(p3[j]);
                    continue;
                    }
                if ((a<=w)&&(b>=w))                                         // cross section -> t0
                    {
                    t0.num=0;
                    i0=0; if (p0[N]<w-_zero) i0=1; if (p0[N]>w+_zero) i0=2;
                    i1=0; if (p1[N]<w-_zero) i1=1; if (p1[N]>w+_zero) i1=2;
                    i2=0; if (p2[N]<w-_zero) i2=1; if (p2[N]>w+_zero) i2=2;
                    i3=0; if (p3[N]<w-_zero) i3=1; if (p3[N]>w+_zero) i3=2;
                    if (i0+i1==3){ a=(w-p0[N])/(p1[N]-p0[N]); for (j=0;j<n;j++) t0.add(p0[j]+a*(p1[j]-p0[j])); }
                    if (i1+i2==3){ a=(w-p1[N])/(p2[N]-p1[N]); for (j=0;j<n;j++) t0.add(p1[j]+a*(p2[j]-p1[j])); }
                    if (i2+i0==3){ a=(w-p2[N])/(p0[N]-p2[N]); for (j=0;j<n;j++) t0.add(p2[j]+a*(p0[j]-p2[j])); }
                    if (i0+i3==3){ a=(w-p0[N])/(p3[N]-p0[N]); for (j=0;j<n;j++) t0.add(p0[j]+a*(p3[j]-p0[j])); }
                    if (i1+i3==3){ a=(w-p1[N])/(p3[N]-p1[N]); for (j=0;j<n;j++) t0.add(p1[j]+a*(p3[j]-p1[j])); }
                    if (i2+i3==3){ a=(w-p2[N])/(p3[N]-p2[N]); for (j=0;j<n;j++) t0.add(p2[j]+a*(p3[j]-p2[j])); }
                    if (!i0) for (j=0;j<n;j++) t0.add(p0[j]);
                    if (!i1) for (j=0;j<n;j++) t0.add(p1[j]);
                    if (!i2) for (j=0;j<n;j++) t0.add(p2[j]);
                    if (!i3) for (j=0;j<n;j++) t0.add(p3[j]);
                    if (t0.num==n1) for (j=0;j<t0.num;j++) S1.add(t0.dat[j]);// copy t0 to target simplex based on points count
                    if (t0.num==n2) for (j=0;j<t0.num;j++) S2.add(t0.dat[j]);
                    if (t0.num==n3) for (j=0;j<t0.num;j++) S3.add(t0.dat[j]);
                    if (t0.num==n4) for (j=0;j<t0.num;j++) S4.add(t0.dat[j]);
                    }
                }
            }
        }
    glColor4ubv((BYTE*)(&col));
    if (render==_render_Wireframe)
        {
        // add points from higher primitives
        for (i=0;i<S2.num;i++) S1.add(S2.dat[i]);
        for (i=0;i<S3.num;i++) S1.add(S3.dat[i]);
        for (i=0;i<S4.num;i++) S1.add(S4.dat[i]);
        glPointSize(5.0);
        glBegin(GL_POINTS);
        glNormal3d(0.0,0.0,1.0);
        if (n==2) for (i=0;i<S1.num;i+=n1) glVertex2dv(S1.dat+i);
        if (n>=3) for (i=0;i<S1.num;i+=n1) glVertex3dv(S1.dat+i);
        glEnd();
        glPointSize(1.0);
        glBegin(GL_LINES);
        glNormal3d(0.0,0.0,1.0);
        if (n==2)
            {
            for (i=0;i<S2.num;i+=n1) glVertex2dv(S2.dat+i);
            for (i=0;i<S3.num;i+=n3)
                {
                glVertex2dv(S3.dat+i+n0); glVertex2dv(S3.dat+i+n1);
                glVertex2dv(S3.dat+i+n1); glVertex2dv(S3.dat+i+n2);
                glVertex2dv(S3.dat+i+n2); glVertex2dv(S3.dat+i+n0);
                }
            for (i=0;i<S4.num;i+=n4)
                {
                glVertex2dv(S4.dat+i+n0); glVertex2dv(S4.dat+i+n1);
                glVertex2dv(S4.dat+i+n1); glVertex2dv(S4.dat+i+n2);
                glVertex2dv(S4.dat+i+n2); glVertex2dv(S4.dat+i+n0);
                glVertex2dv(S4.dat+i+n0); glVertex2dv(S4.dat+i+n3);
                glVertex2dv(S4.dat+i+n1); glVertex2dv(S4.dat+i+n3);
                glVertex2dv(S4.dat+i+n2); glVertex2dv(S4.dat+i+n3);
                }
            }
        if (n>=3)
            {
            for (i=0;i<S2.num;i+=n1) glVertex3dv(S2.dat+i);
            for (i=0;i<S3.num;i+=n3)
                {
                glVertex3dv(S3.dat+i+n0); glVertex3dv(S3.dat+i+n1);
                glVertex3dv(S3.dat+i+n1); glVertex3dv(S3.dat+i+n2);
                glVertex3dv(S3.dat+i+n2); glVertex3dv(S3.dat+i+n0);
                }
            for (i=0;i<S4.num;i+=n4)
                {
                glVertex3dv(S4.dat+i+n0); glVertex3dv(S4.dat+i+n1);
                glVertex3dv(S4.dat+i+n1); glVertex3dv(S4.dat+i+n2);
                glVertex3dv(S4.dat+i+n2); glVertex3dv(S4.dat+i+n0);
                glVertex3dv(S4.dat+i+n0); glVertex3dv(S4.dat+i+n3);
                glVertex3dv(S4.dat+i+n1); glVertex3dv(S4.dat+i+n3);
                glVertex3dv(S4.dat+i+n2); glVertex3dv(S4.dat+i+n3);
                }
            }
        glEnd();
        }
    if (render==_render_Polygon)
        {
        double nor[3],a[3],b[3],q;
        #define _triangle2(ss,p0,p1,p2)                 \
            {                                           \
            glVertex2dv(ss.dat+i+p0);                   \
            glVertex2dv(ss.dat+i+p1);                   \
            glVertex2dv(ss.dat+i+p2);                   \
            }
        #define _triangle3(ss,p0,p1,p2)                 \
            {                                           \
            for(j=0;(j<3)&&(j<n);j++)                   \
                {                                       \
                a[j]=ss.dat[i+p1+j]-ss.dat[i+p0+j];     \
                b[j]=ss.dat[i+p2+j]-ss.dat[i+p1+j];     \
                }                                       \
            for(;j<3;j++){ a[j]=0.0; b[j]=0.0; }        \
            nor[0]=(a[1]*b[2])-(a[2]*b[1]);             \
            nor[1]=(a[2]*b[0])-(a[0]*b[2]);             \
            nor[2]=(a[0]*b[1])-(a[1]*b[0]);             \
            q=sqrt((nor[0]*nor[0])+(nor[1]*nor[1])+(nor[2]*nor[2]));    \
            if (q>1e-10) q=1.0/q; else q-0.0;           \
            for (j=0;j<3;j++) nor[j]*=q;                \
            glNormal3dv(nor);                           \
            glVertex3dv(ss.dat+i+p0);                   \
            glVertex3dv(ss.dat+i+p1);                   \
            glVertex3dv(ss.dat+i+p2);                   \
            }
        #define _triangle3b(ss,p0,p1,p2)                \
            {                                           \
            glNormal3dv(nor3.dat+(i/n));                \
            glVertex3dv(ss.dat+i+p0);                   \
            glVertex3dv(ss.dat+i+p1);                   \
            glVertex3dv(ss.dat+i+p2);                   \
            }
        glBegin(GL_TRIANGLES);
        if (n==2)
            {
            glNormal3d(0.0,0.0,1.0);
            for (i=0;i<S3.num;i+=n3) _triangle2(S3,n0,n1,n2);
            for (i=0;i<S4.num;i+=n4)
                {
                _triangle2(S4,n0,n1,n2);
                _triangle2(S4,n3,n0,n1);
                _triangle2(S4,n3,n1,n2);
                _triangle2(S4,n3,n2,n0);
                }
            }
        if (n>=3)
            {
            for (i=0;i<S3.num;i+=n3) _triangle3 (S3,n0,n1,n2);
            for (i=0;i<S4.num;i+=n4)
                {
                _triangle3(S4,n0,n1,n2);
                _triangle3(S4,n3,n0,n1);
                _triangle3(S4,n3,n1,n2);
                _triangle3(S4,n3,n2,n0);
                }
            glNormal3d(0.0,0.0,1.0);
            }
        glEnd();
        #undef _triangle2
        #undef _triangle3
        }
    #undef _swap
    }
//---------------------------------------------------------------------------
#undef _cube
//---------------------------------------------------------------------------
#endif
//---------------------------------------------------------------------------

我使用动态列表模板的方式如下： List<double> xxx;与double xxx[];相同
xxx.add(5);将5添加到列表结尾
xxx[7]访问数组元素（安全）
xxx.dat[7]访问数组元素（不安全但直接访问速度快）
xxx.num是数组的实际使用大小
xxx.reset()清除数组并设置xxx.num=0
xxx.allocate(100)预先分配100个项目的空间

因此，您需要将其移植到任何可用的列表中（例如std:vector<>）。我还使用了5x5转换矩阵，其中：

void ND_reper::g2l    (vector<4> &l,vector<4> &g);  // global xyzw -> local xyzw
void ND_reper::l2g    (vector<4> &g,vector<4> &l);  // global xyzw <- local xyzw

将点转换为全局或本地坐标（通过将直接或反向矩阵乘以点）。由于其仅在渲染中使用一次，因此您可以忽略它并复制点（无旋转）... 在同一标题中还有一些常量：

const double pi   =    M_PI;
const double pi2  =2.0*M_PI;
const double pipol=0.5*M_PI;
const double deg=M_PI/180.0;
const double rad=180.0/M_PI;

我还整合了向量和矩阵数学模板到变换矩阵头文件中，因此vector<n>是n维向量，matrix<n>是n*n的方阵，但仅用于渲染，因此您可以忽略它。如果您感兴趣，这里有一些链接，从中得出了所有这些内容：

• 如何使用4d旋转器
• ND向量和方阵数学模板

枚举和尺寸缩小仅用于渲染。 cfg保存每个维度应如何缩减为2D。

AnsiString是来自VCL的自我重定位字符串，因此请使用您的环境中提供的char*或string类。 DWORD只是无符号32位整数。希望我没有忘记什么...

- Spektre

---

我已经颁发了悬赏，因为这看起来是最有前途的解决方案，并且悬赏即将到期。然而，由于未声明的变量，我无法运行此代码，您能否解决这个问题？ - F Chopin

@Karl 我添加了[edit1]，包含更多（缺失的）代码和描述。我没有发布其他网格的代码，因为我担心我接近答案的30K限制（网格的完整代码有23KB，不包括辅助文件），如果你还缺少其他内容，请在评论中提醒我。 - Spektre

@Karl，我刚刚稍微更新了一下代码（为3D和4D提供更好的螺旋和点比率）。 - Spektre

Answer 2

之前的回答都是正确的，但缺乏实际代码。有两个真正的缺失部分，这里一般实现了它们。

1. 我们需要计算 sin^(d-2)(x) 的积分。如果使用递归分部法，则此函数具有封闭形式。在这里，我以递归方式实现它，但对于维数 ~> 100，我发现 sin^d 的数值积分速度更快。
2. 我们需要计算该积分的反函数，在 sin^d 中，当 d > 1 时没有一个封闭的形式。在这里，我使用二分查找来计算它，尽管其他答案中可能有更好的方式。

这两个步骤结合生成素数的方法就形成了完整的算法：

from itertools import count, islice
from math import cos, gamma, pi, sin, sqrt
from typing import Callable, Iterator, List

def int_sin_m(x: float, m: int) -> float:
    """Computes the integral of sin^m(t) dt from 0 to x recursively"""
    if m == 0:
        return x
    elif m == 1:
        return 1 - cos(x)
    else:
        return (m - 1) / m * int_sin_m(x, m - 2) - cos(x) * sin(x) ** (
            m - 1
        ) / m

def primes() -> Iterator[int]:
    """Returns an infinite generator of prime numbers"""
    yield from (2, 3, 5, 7)
    composites = {}
    ps = primes()
    next(ps)
    p = next(ps)
    assert p == 3
    psq = p * p
    for i in count(9, 2):
        if i in composites:  # composite
            step = composites.pop(i)
        elif i < psq:  # prime
            yield i
            continue
        else:  # composite, = p*p
            assert i == psq
            step = 2 * p
            p = next(ps)
            psq = p * p
        i += step
        while i in composites:
            i += step
        composites[i] = step

def inverse_increasing(
    func: Callable[[float], float],
    target: float,
    lower: float,
    upper: float,
    atol: float = 1e-10,
) -> float:
    """Returns func inverse of target between lower and upper

    inverse is accurate to an absolute tolerance of atol, and
    must be monotonically increasing over the interval lower
    to upper    
    """
    mid = (lower + upper) / 2
    approx = func(mid)
    while abs(approx - target) > atol:
        if approx > target:
            upper = mid
        else:
            lower = mid
        mid = (upper + lower) / 2
        approx = func(mid)
    return mid

def uniform_hypersphere(d: int, n: int) -> List[List[float]]:
    """Generate n points over the d dimensional hypersphere"""
    assert d > 1
    assert n > 0
    points = [[1 for _ in range(d)] for _ in range(n)]
    for i in range(n):
        t = 2 * pi * i / n
        points[i][0] *= sin(t)
        points[i][1] *= cos(t)
    for dim, prime in zip(range(2, d), primes()):
        offset = sqrt(prime)
        mult = gamma(dim / 2 + 0.5) / gamma(dim / 2) / sqrt(pi)

        def dim_func(y):
            return mult * int_sin_m(y, dim - 1)

        for i in range(n):
            deg = inverse_increasing(dim_func, i * offset % 1, 0, pi)
            for j in range(dim):
                points[i][j] *= sin(deg)
            points[i][dim] *= cos(deg)
    return points

在球体上生成200个点，将产生以下图像：

- Erik

---

根据您的回答，我优化了代码，使其能够在高维空间中（大约）生成许多点（300维上的30000个点需要大约23秒）。请参见https://pastebin.com/YPpVJMkc。 - Wakeme UpNow

Answer 3

我有另一个疯狂的想法来做这件事。它完全不同于我的以前的方法，因此是一个新答案...

好吧，其他答案之一建议在超立方体表面创建点的均匀分布，然后将点距离超立方体中心的距离归一化为超空间的半径，并将其用于排斥粒子模拟。我过去在3D中尝试过，效果很好，但在更高的维度中，这将变得非常缓慢或者需要使用类似BVH的结构进行复杂处理。

但是这让我想到了反向操作。因此，将点非线性地分布在超立方体上，使得在归一化后，点在超球面上线性分布...

让我们从简单的2D开始。

所以我们只需要在+/-45度之间步进角度并计算绿色点。角度步长da必须完全除尽90度并给出点密度。因此，所有的2D点都将是+/-1.0和tan(angle)的组合，适用于所有面。

当所有点都完成后，只需计算每个点到中心的大小并重新缩放它，使其等于超球体半径。

这可以轻松地扩展到任何维数。

对于高于2D的每个维度，只需添加一个循环角度即可。

以下是使用我先前回答中的引擎的C++示例，适用于2D、3D和4D：

void ND_mesh::set_HyperSpherePCL(int N,double r,double da)
    {
    reset(N);

    int na=floor(90.0*deg/da);
    if (na<1) return;
    da=90.0*deg/double(na-1);

    if (n==2)
        {
        int i;
        double a,x,y,l;
        for (a=-45.0*deg,i=0;i<na;i++,a+=da)
            {
            x=tan(a); y=1.0;
            l=sqrt((x*x)+(y*y));
            x/=l; y/=l;
            pnt.add( x); pnt.add(-y);
            pnt.add( x); pnt.add(+y);
            pnt.add(-y); pnt.add( x);
            pnt.add(+y); pnt.add( x);
            }
        }
    if (n==3)
        {
        int i,j;
        double a,b,x,y,z,l;
        for (a=-45.0*deg,i=0;i<na;i++,a+=da)
         for (b=-45.0*deg,j=0;j<na;j++,b+=da)
            {
            x=tan(a); y=tan(b); z=1.0;
            l=sqrt((x*x)+(y*y)+(z*z));
            x/=l; y/=l; z/=l;
            pnt.add( x); pnt.add( y); pnt.add(-z);
            pnt.add( x); pnt.add( y); pnt.add(+z);
            pnt.add( x); pnt.add(-z); pnt.add( y);
            pnt.add( x); pnt.add(+z); pnt.add( y);
            pnt.add(-z); pnt.add( x); pnt.add( y);
            pnt.add(+z); pnt.add( x); pnt.add( y);
            }
        }
    if (n==4)
        {
        int i,j,k;
        double a,b,c,x,y,z,w,l;
        for (a=-45.0*deg,i=0;i<na;i++,a+=da)
         for (b=-45.0*deg,j=0;j<na;j++,b+=da)
          for (c=-45.0*deg,k=0;k<na;k++,c+=da)
            {
            x=tan(a); y=tan(b); z=tan(c); w=1.0;
            l=sqrt((x*x)+(y*y)+(z*z)+(w*w));
            x/=l; y/=l; z/=l; w/=l;
            pnt.add( x); pnt.add( y); pnt.add( z); pnt.add(-w);
            pnt.add( x); pnt.add( y); pnt.add( z); pnt.add(+w);
            pnt.add( x); pnt.add( y); pnt.add(-w); pnt.add( z);
            pnt.add( x); pnt.add( y); pnt.add(+w); pnt.add( z);
            pnt.add( x); pnt.add(-w); pnt.add( y); pnt.add( z);
            pnt.add( x); pnt.add(+w); pnt.add( y); pnt.add( z);
            pnt.add(-w); pnt.add( x); pnt.add( y); pnt.add( z);
            pnt.add(+w); pnt.add( x); pnt.add( y); pnt.add( z);
            }
        }

    for (int i=0;i<pnt.num/n;i++) as1(i);
    rescale(r,n);
    }
//---------------------------------------------------------------------------

"

n=N是维度，r是半径，da是角度步长（以弧度表示）。

并且有2D/3D/4D预览：

"

这里有更多的点和更好的3D尺寸：

“方块图案略微可见，但是点距离看起来还可以。在 GIF 上很难看到它，因为背面的点与前面的点合并了……”“这是未经球形归一化的二维正方形和三维立方体：”

如您所见，边缘上的点密度要小得多...

预览仅使用透视投影，因为这不会生成网格拓扑结构，只是点，所以无法进行横截面操作...

此外，请注意，这会在边缘上产生一些重复的点（我认为对于某些镜子，将角度循环迭代少一次应该可以解决这个问题，但我太懒了没有实现）

我强烈建议阅读以下内容：

• 使用高斯分布PRNG在球体上均匀分布点

- Spektre

Answer 4

我们有n个点，它们分别是P1, ..., Pn。我们有一个维度数d。每个(i = 1,n)点可以表示为：

Pi = (pi(x1), ..., pi(xd))

我们知道

D(Pi,0) = 1 <=> sqrt((pi(x1) - pj(x1))^2 + ... + (pi(xd) - pj(xd))^2) = 1

并且任何两个点之间的最小距离MD是

MD <= D(Pi, Pj)

只有当MD不能更高时才接受解决方案。

如果d = 2，则我们有一个圆并在其上放置点。该圆是具有以下属性的多边形：

- 它有n个角 - n -> 无穷大 - 每条边长度相似

因此，一个拥有n个角的多边形（其中n是有限且大于2的数字，并且每条边的长度相似）在我们增加n的时候越来越接近于一个圆。请注意，在d = 2时，第一个多边形是三角形。我们有一个单一的角度，最小的角度单位为360度/n。

现在，如果我们有一个正方形并均匀地分布点在上面，那么通过基础变换将我们的正方形转换为圆形应该是精确解或非常接近精确解。如果这是精确解，那么这就是当d = 2时的简单解决方案。如果它仅仅是非常接近，那么通过逼近的方法，我们可以在给定您选择的精度范围内确定解决方案。

我会将这个想法用于当d = 3时的情况。我会解决立方体的问题，因为这个问题要简单得多，然后使用基础变换将我的立方体点转换为球面点。我会在d > 3上使用这种方法，解决超立方体的问题并将其转换为超球体。在您均匀分布d维超立方体上的点时，请使用曼哈顿距离。

请注意，我不知道将超立方体转换为超球体的解决方案是否为确切解决方案，还是仅仅接近于它，但如果这不是确切解决方案，则我们可以通过近似来增加精度。

因此，这种方法是解决问题的一种方法，但在时间复杂度方面不一定是最佳方法，因此，如果有人深入研究了斐波那契晶格区域，并知道如何将其推广到更多维度，则他/她的答案可能比我的更好。

如果您定义了f（x）= x-0.5sin2x的 Taylor系列，则可以确定其反演。 您将得到一个可逆的x的多项式系列 。

- Lajos Arpad

---

我们在超立方体的表面均匀分布点，然后将其转换为超球体，我们调整所有点从原点到端点的向量长度为1。除非我误解了您所说的基础变换，否则这将导致点在超立方体角落处更加密集。 - F Chopin

@Karl 我同意你的看法，这个解决方案可能不太可行（就如你所说的），但也许可以用来设置粒子排斥方法中所提到的初始状态。如果初始状态分布良好，那么收敛到最优状态的速度可能会更快。 - John Coleman

@JohnColeman 我已经研究了4年的粒子排斥方法来解决这个问题。我研究的其中一个领域是使用在这个答案中描述的技术来种植粒子排斥方法（如果我正确理解了基础变换）。结果还不错，但现在我希望研究确定性方法，这就是为什么我想专注于斐波那契晶格的原因。 - F Chopin

@Karl，根据我的想法，我们不使用欧几里得几何来计算点之间的距离，而是使用曼哈顿距离（将不同维度的距离相加）。当然，这只是一个起点。如果这导致根据规格的确定性等分布，则这是一种解决方案。如果不是，则这是一个很好的起点，但在这种情况下是不确定的。如果有人有时间检查初始结果是否符合标准，如果不符合标准，离标准还有多远，那就太好了。 - Lajos Arpad

@LajosArpad 看起来确实是一个有前途的开始。 - John Coleman

Answer 5

作为部分答案，您可以使用牛顿法来计算f的反函数。在牛顿迭代中使用x作为初始点是一个不错的选择，因为f(x)从未超过x 1个单位。以下是Python实现：

import math

def f(x):
    return x + 0.5*math.sin(2*x)

def f_inv(x,tol = 1e-8):
    xn = x
    y = f(xn)
    while abs(y-x) > tol:
        xn -= (y-x)/(1+math.cos(2*xn))
        y = f(xn)
    return xn

牛顿迭代法的一个好处是，当cos(2*x) = -1时（即除数为0的情况），你自动有sin(2*x) = 0，因此f(x) = x。在这种情况下，while循环永远不会执行，f_inv只需返回原始x即可。

- John Coleman

---

很好，这样就很好地解决了反函数的问题。唯一剩下的问题是如何为任意d生成角度公式。 - F Chopin

简洁而优美的实现。 - Lajos Arpad