使用指数平滑法和不规则事件来估计事件发生的速率

Question

使用指数平滑法和不规则事件来估计事件发生的速率

18

Imagine that I have a set of measurements of x that are taken by many processes x₀ ... x_N at times t₀ ... t_N. Let's assume that at time t I want to make an estimate of the current value of x, based on the assumption that there is no long-term trend I know about and that x can be predicted from an algorithm such as exponential smoothing. As we have many processes, and N can get very large, I can't store more than a few values (e.g. the previous state).

One approach here would be to adapt the normal exponential smoothing algorithm. If samples are taken regularly, I would maintain an estimator y_n such that: y_n = α.y_n-1 + ( 1 - α ). x_n 这种方法在抽样不规则时并不理想，因为许多样本在一起会产生不成比例的影响。因此，该公式可以改为：

y_n = α_n.y_n-1 + ( 1 - α_n ). x_n 其中，

α_n = e^{-k.(t_n - t_n-1)} 即根据前两个样本之间的时间间隔动态调整平滑常数。我对这种方法感到满意，并且它似乎有效。这是here给出的第一个答案，并且Eckner在2012年的论文（PDF）中提供了这些技术的良好概述。

现在，我的问题如下。我想将上述内容适应于评估事件发生的速率。偶尔会发生某个事件。使用类似的指数技术，我想要得到该事件发生的速率的估计值。

两种明显的策略是： 1. 使用上一个事件之间的延迟作为数据序列 xn 来使用第一个或第二个技术。 2. 使用上一个事件之间的延迟的倒数（即速率）作为数据序列 xn 来使用第一个或第二个技术。

据我所知，这两种策略都不是好的策略。首先，考虑每500ms发生一次事件（一方面），而另一方面则是200ms和800ms的延迟后才发生一次事件。很明显，它们每秒都会发生两次，因此给出的速率估计应该是相同的。忽略最后一个样本的时间似乎是愚蠢的，因此我将专注于第二个策略。使用延迟（而不是倒数）并不是一个好的预测因素，因为模拟200ms / 800ms的样本流产生了约1.5的估计值（基于倒数的平均值不是平均数的倒数）。

但是，更为重要的是，这两种策略都无法应对实际情况，即突然所有事件停止了很长一段时间。因此，y的“最新”值是上一个事件的值，因此速率的估计从未被计算过。因此，速率看起来是恒定的。当然，如果我是在事后分析数据，这不会成为问题，但我正在实时分析它。

我意识到另一种方法是定期运行一些线程（例如每10秒），并计算此10秒间隔内发生的事件数。这对我的资源非常消耗，因为统计数据通常不需要，而且由于互斥问题，我不愿运行轮询所有内容的线程。因此，我想（某种方式）使用调整状态读取的算法（例如）自上次采样以来的时间。这似乎是一个合理的方法，因为如果性能是在与样本独立选择的时间测量的话，测量时间将平均位于样本之间时间段的中点，因此未经平滑处理的速率估计值将是自上次采样以来的时间的倒数的一半。为了使事情更加复杂，我的测量时间将不独立于样本。

我感觉这个问题的答案很简单，但是它却让我无法理解。我觉得正确的方法是假设事件服从泊松分布，并根据上一个样本以及某种形式的移动平均值来推导出λ的估计值，但我的统计学知识太生疏了，无法使其有效运作。

这个问题有一个相似的问题here，但答案似乎并不令人满意（希望我解释清楚了）。我还想补充一下，卡尔曼滤波器似乎过于繁重，因为我只需要估计一个变量，并且对它一无所知。还有其他一些类似的问题，其中大部分建议保留大量的值（从内存角度来看这不现实），或者没有解决以上两个问题。

- abligh

@RamanShah 事件应该以大致恒定的速率（短期内可能服从泊松分布）来自多个来源，导致一个不错的稳定平均值。我试图衡量的是（a）这些事件的大幅下降，表明存在严重的连接问题，（b）在稳态条件下相对准确的“速率”，以便有东西可以用来衡量性能。您可以将其视为具有许多接口的网络设备上的接口计数器。 - abligh

那么，为了澄清一下，当您很长时间没有看到事件时，您希望您的估算器衰减为零？我认为我开始理解您的数据以及您想要从中获得的内容，但我不确定。 - Raman Shah

1

这里有一篇论文，涉及到估计非齐次泊松过程的参数的情况，同时也提到了速率趋近于零的问题。 - Daniel Brückner

@DanielBrückner 谢谢。看起来非常有用。我会阅读的。与此同时，你给了我一个想法，我将在下面发布。 - abligh

在我发表第一条评论之前，我并没有完全阅读这篇论文。我的想法是保留最后n个事件，当你想知道当前速率时，从最后n次发生和自上次发生以来的时间计算它。因此，您将不会有一个包含当前速率的变量，而是在需要时计算它，并可能缓存结果一段时间，以防经常使用。 - Daniel Brückner

显示剩余5条评论

2个回答

2

你可以尝试以下方法：

保留一个估计器 z_n，使得在每个事件发生时：

z_n = (z_n-1+κ).e^{-κ.(t_n-t_n-1)} 这将收敛于每秒的事件率。稍微更好的估计器是（如果你在事件之前或之后计算估计值仍然存在误差/噪声）：

w_n = z_n.e^-κ/(2.z_n) 在你的例子中，它将收敛于2s^-1（500ms的倒数）。常数κ负责平滑处理，单位为s^-1。小的值将平滑更多。如果你的事件速率大约为每秒，那么0.01s-1的值对于κ来说是一个很好的开始。

这种方法有一个起始偏差，z₀可以设置为一个值的估计，以加快收敛速度。小的κ值将保持偏差更长时间。

还有更强大的分析泊松分布的方法，但它们通常需要大缓冲区。频率分析如傅里叶变换就是其中之一。

- galinette

这基本上与我提供的公式相同，只是你在追踪平均值时是在最近事件之前，而我是在最近事件之后追踪平均值。当然，任何一种方法都可以；它们只是* k *不同而已。无论如何，+1 表示你更快。 :-) - Ilmari Karonen

至少你证明了它，我没有 :) （我只是凭直觉做的，并在随机系列上进行了检查...） - galinette

经过最后一次编辑，我的更准确，因为它补偿了与间隔相关的偏差。 - galinette

看起来你现在计算的东西和我略有不同：我的λ*是最近事件速率的简单指数加权平均值，如果没有新事件发生，它将指数级地衰减到零，而你似乎是从最后一个事件向前进行投影以计算“平均值的平均值”（只有在事件发生时你的估计才会改变）。我想，如果每个事件的平均值的不连续性被认为是不可取的，我也可以在公式中添加某种平滑项；我还需要再考虑一下…… - Ilmari Karonen

你能解释一下w sub n的推导过程吗？如果在最后一个样本时间之后进行估计，你会如何进行调整？ - abligh

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- Ilmari Karonen · Accepted Answer

首先，如果您假设事件本身的发生率是恒定的（或者您只关心其长期平均值），那么您可以简单地估计它为：

λ* = N / (t − t₀)

其中，t 是当前时间，t₀ 是观测开始时间，N 是自 t₀ 起观察到的事件数量，λ* 是真实频率 λ 的估计。

此时，有必要注意，上述估计公式可以改写为积分形式：

λ* = integral( δ_event(τ) dτ ) / integral( 1 dτ )

其中积分变量τ的范围从t₀到t，δ_event(τ) = sum( δ(τ − t_i), i = 1 .. N )是狄拉克δ函数的和，每个事件i的发生时间t_i处有一个单独的delta峰。

当然，这将是一种完全无用的计算λ*的方式，但事实证明这是一个概念上有用的公式。基本上，观察这个公式的方法是，函数δ_event(τ)测量在时间τ时事件数量增加的瞬时速率，而第二个被积函数（只是常数1）测量时间随时间增加的速率（当然，这只是每秒钟增加一秒）。

好的，但是如果频率λ本身可能随时间变化，并且您想要估计其当前值，或者至少是最近一段时间的平均值，该怎么办？使用上面给出的积分比公式，我们可以通过将两个积分加权来得到这样的估计值，加权函数w(τ)偏向于最近的时间：

λ*_recent = integral( δ_event(τ) w(τ) dτ ) / integral( w(τ) dτ )

现在，唯一需要做的就是选择一个合理的w(τ)，使得这些积分简化为易于计算的内容。事实证明，如果我们选择一个指数衰减的加权函数，形式为w(τ) = exp(k(τ − t))，其中k是衰减速率，则积分简化为：

λ*_recent = sum( exp(k(t_i − t)), i = 0 .. N ) k / ( 1 − exp(k(t₀ − t)) )

当 t₀ → −∞ 时（即，在实践中，当总观测时间（t − t₀）远大于权重衰减时间尺度 1/k 时），这进一步简化为：

λ*_recent = k sum( exp(k(t_i − t)), i = 0 .. N )

很遗憾，天真地应用这个公式仍需要我们记住所有事件时间t_i。然而，我们可以使用与计算常规指数加权平均值相同的技巧——在较早时间t'处给出加权平均事件率λ*_recent_*(t')，并假设在t'和t之间没有发生新事件，我们可以简单地计算当前加权平均事件率λ*_recent_*(t)为：

λ*_recent(t) = exp(k(t' - t)) λ*_recent(t')

此外，如果我们现在观察到一个恰好发生在时间t的新事件，那么事件后的加权平均事件率将变为：

λ*_recent(t) = k + exp( k(t' − t) ) λ*_recent(t')

因此，我们得出一个非常简单的规则：我们需要存储的是上一个观察事件的时间t_last和在该事件之后估计的最近事件率λ*_last。（例如，我们可以将它们初始化为t_last = t₀和λ*_last = 0; 实际上，对于λ*_last = 0，t_last的值没有影响，但对于非零λ*_last，它会有影响。）

每当发生新事件（在时间t_new），我们更新这些值如下：

λ*_last ← k + exp( k(t_last − t_new) ) λ*_last t_last ← t_new 每当我们想要知道当前时间的最近事件率平均值时，我们只需按以下方式计算：

λ*（）= exp（（_last - ））λ*_last

提示：为了纠正对t_last（任意的初始值）的初始偏差，我们可以添加回之前简化的 1 / ( 1 − exp(k(t₀ − t)) ) 校正项。要做到这一点，只需从t_last = 0开始，在t = t₀时更新t_last，但计算时间t的估计事件率平均值如下：

λ*_corr(t) = exp( k(t_last − t) ) λ*_last / ( 1 − exp(k(t₀ − t)) )

(这里，t₀表示您开始测量事件的时间，而不是第一个事件的发生时间。)

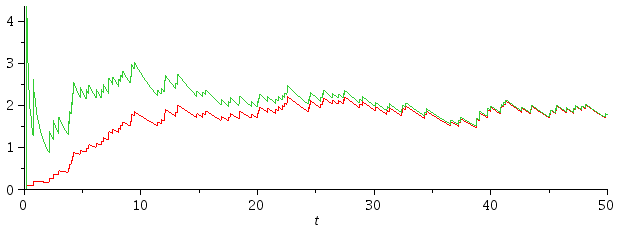
这将消除对零的初始偏差，但代价是增加早期方差。以下是一个示例图，显示了进行校正的效果，其中 k = 0.1，真实平均事件率为2： Plot of λ* over time, with or without initial bias correction

红线显示没有进行初始偏差校正的 λ*(t)（从 λ*(t₀) = 0 开始），而绿线显示经过校正的估计值 λ*_corr(t)。

Pps. 如上图所示，λ*并非时间的连续函数：每当事件发生时，它会跃升k，在未发生事件时指数衰减至零。

如果您希望得到更平滑的估计值，则可以计算λ*本身的指数衰减平均值：

λ**(t) = integral( λ*(τ) exp(k₂(τ − t)) dτ ) / integral( exp(k₂(τ − t)) dτ )

其中，λ*是如上所述的指数衰减平均事件率，k₂是第二个平均值的衰减率，积分范围为−∞ ≤ τ ≤ t。

此积分也可以通过以上的逐步更新规则进行计算：

λ_last ← W(Δt) λ*_last + exp(−k₂ Δt) λ_last*
λ*_last ← k₁ + exp(−k₁ Δt) λ*_last
t_last ← t_new

其中 k₁ 和 k₂ 是第一和第二平均值的衰减率，Δt=t_new − t_last 是事件之间的经过时间，且：

如果k₁ ≠ k₂，则：

W(Δt) = k₂ ( exp( −k₂ Δt ) − exp( −k₁ Δt ) ) / (k₁ − k₂)

如果k₁ = k₂ = k，则：

W(Δt) = k Δt exp( −k Δt ) （当(k₁ − k₂) → 0时，后一个式子由前者的极限得出。）

要计算任意时间点t的第二个平均值，请使用相同的公式：

λ**(t) = W(Δt) λ*_last + exp( −k₂ Δt ) λ**_last

除了Δt = t − t_last之外，不要更改任何内容。

如上所述，这个估计值也可以通过应用合适的时间依赖缩放因子进行偏差校正：

λ**_corr(t) = λ**(t) / (1 - S(t − t₀))

其中： S(Δt) = ( k₁ exp( −k₂ Δt ) − k₂ exp( −k₁ Δt ) ) / (k₁ − k₂)

如果k₁ ≠ k₂，或者

S(Δt) = (1 + k Δt) exp( −k Δt )

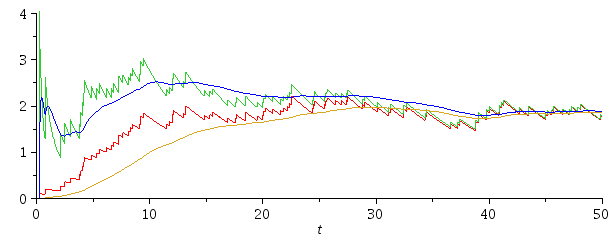
如果k₁ = k₂ = k，则如上所述，下图显示了平滑的效果。红色和绿色线条显示λ*(t)和λ*_corr(t)，而黄色和蓝色线条显示λ**(t)和λ**_corr(t)，使用k₁ = 0.1（如上所述）和k₂ = 0.2进行计算：

Plot of λ* and λ** over time, with or without initial bias correction