移动点和移动线段的撞击位置和时间（连续碰撞检测）

Question

我正在开发一个2D碰撞系统，将形状分解为一种可能的基元：由两个点定义的不可穿透线段。为了为此系统提供碰撞检测，我使用一种静态碰撞检测方法，每帧计算一个线段边缘与当前处理的线段（点/线距离）之间的距离。如果距离太小，则在该帧期间触发碰撞。这很好用，但已知问题是如果一个或多个物体表现出高速度，则会出现隧道效应。因此，我正在尝试其他选择。

现在我想引入连续碰撞检测（CCD），它可以操作动态点/动态线段。我的问题是：我不确定该如何实现。我知道如何在两个移动点之间进行连续碰撞、移动点和静态线段之间进行连续碰撞，但不知道如何在移动点（由点P定义）和移动线段（由点U和V定义，两者都可以完全自由移动）之间进行CCD。 问题示意图 我看到类似的问题在SO和其他平台上被问过，但没有这些确切的要求。

• 点和线段都在移动
• 线段可以旋转和拉伸（因为 U 和 V 自由移动）
• 需要在两帧之间准确地找到碰撞时间和碰撞点（CCD，无静态碰撞测试）
• 如果可能，我更喜欢数学上完美的解决方案（没有迭代逼近算法，扫描体积）
• 注意：扫描线形状不总是一个凸多边形，因为 U、V 点的自由度（见图像）
• 注意：使用扫描体积测试进行碰撞检测是不准确的，因为与多边形相交的碰撞点并不意味着实际运动中的碰撞点（见图像，一旦实际线段越过点的轨迹，该点就已经离开了多边形）

到目前为止，我想出了以下方法，假设：

• sP (帧开始时的P),
• eP (帧结束时的P),
• sU (帧开始时的U),
• eU (帧结束时的U),
• sV (帧开始时的V),
• eV (帧结束时的V)

问题: 它们会碰撞吗？如果是，何时和在哪里？

为了回答“是否”的问题，我发现这篇论文很有用：https://www.cs.ubc.ca/~rbridson/docs/brochu-siggraph2012-ccd.pdf（第3.1节），但我无法得出“何时”和“在哪里”的答案。 我也在这里找到了一个替代性的解释：http://15462.courses.cs.cmu.edu/fall2018/article/13（第三个问题）。

解决方案:

将每个点在帧期间的时间轨迹建模为线性运动（对于 0 <= t <= 1 的线路轨迹）。

• P(t) = sP * (1 - t) + eP * t
• U(t) = sU * (1 - t) + eU * t
• V(t) = sV * (1 - t) + eV * t

（0 <= a <= 1 表示由 U 和 V 定义的线段上的位置）：

• UV(a, t) = U(t) * (1 - a) + V(t) * a

通过等式化点和线段方程来建模碰撞：

• P(t) = UV(a, t)
• P(t) = U(t) * (1 - a) + V(t) * a

导出从点P到线段上一点的向量函数(见F图片):

• F(a, t) = P(t) - (1 - a) * U(t) - a * V(t)

现在需要找到a和t，使得F(a, t) = (0, 0)，且a，t在[0，1]范围内。这可以建模为一个具有2个变量的根查找问题。

将时间轨迹方程插入F(a, t)中：

• F(a, t) = (sP * (1 - t) + eP * t) - (1 - a) * (sU * (1 - t) + eU * t) - a * (sV * (1 - t) + eV * t)

按维度（x和y）分离时间轨迹方程:

• Fx(a, t) = (sP.x * (1 - t) + eP.x * t) - (1 - a) * (sU.x * (1 - t) + eU.x * t) - a * (sV.x * (1 - t) + eV.x * t)

• Fy(a, t) = (sP.y * (1 - t) + eP.y * t) - (1 - a) * (sU.y * (1 - t) + eU.y * t) - a * (sV.y * (1 - t) + eV.y * t)

现在我们有两个方程和两个变量需要求解 (Fx，Fy 分别对应 a，t)，因此我们可以使用求解器来得到 a 和 t，然后再检查它们是否在 [0, 1] 范围内。对吗？

当我将其输入到 Python sympy 中进行求解时：

from sympy import symbols, Eq, solve, nsolve

def main():

    sxP = symbols("sxP")
    syP = symbols("syP")
    exP = symbols("exP")
    eyP = symbols("eyP")

    sxU = symbols("sxU")
    syU = symbols("syU")
    exU = symbols("exU")
    eyU = symbols("eyU")

    sxV = symbols("sxV")
    syV = symbols("syV")
    exV = symbols("exV")
    eyV = symbols("eyV")

    a = symbols("a")
    t = symbols("t")

    eq1 = Eq((sxP * (1 - t) + exP * t) - (1 - a) * (sxU * (1 - t) + exU * t) - a * (sxV * (1 - t) + exV * t))
    eq2 = Eq((syP * (1 - t) + eyP * t) - (1 - a) * (syU * (1 - t) + eyU * t) - a * (syV * (1 - t) + eyV * t))

    sol = solve((eq1, eq2), (a, t), dict=True)

    print(sol)

if __name__ == "__main__":
    main()

我得到了一个解决方案，它非常庞大，花费sympy约5分钟来评估。 我不能在我的实际引擎代码中使用这样一个大表达式，这个解决方案对我来说似乎不正确。 我想知道的是： 我错过了什么吗？我认为这个问题似乎很容易理解，但我无法找到一种数学上准确的方法来找到动态点/动态线段的时间（t）和点（a）的撞击解决方案。任何帮助都将不胜感激，即使有人告诉我这样做是不可能的。

- PawelBoe

Answer 1

简而言之

我读到了“……大约需要5分钟来评估……”

绝不会这么长时间，这是一个实时解决方案，适用于许多行和点。

很抱歉这不是一个完整的答案（我没有理性化和简化方程），这将由您自己完成找到交点的过程。

此外，我可以看到几种解决方法，因为它围绕着一个三角形（见图像），当它变平时即为解决方案。下面的方法是找到三角形的长边等于两个短边之和的时间点。

求解u（时间）

这可以作为一个简单的二次方程来完成，系数来自3个起始点，每个点的单位时间向量。求解u。

下面的图片提供更多细节。

• P点是点的起始位置
• L1，L2点是线段的起点。
• V1向量代表点在单位时间内的位移（沿着绿线）。
• V2，V3向量代表线段两端在单位时间内的位移。
• u是单位时间
• A为蓝色点，B和C为红色线段的端点

可能存在一个时间点u，在这个时间点上，A在线段B，C上。此时，线段AB（用a表示）和AC（用c表示）的长度之和等于线段BC（用b表示）的长度（橙色线段）。

这意味着当 b - (a + c) == 0 时，该点在直线上。在图像中，将点表示为正方形可以简化问题。b² - (a² + c²) == 0 图像底部是关于 u, P, L1, L2, V1, V2, V3 的二次方程。

需要重新排列该方程以获得 (???)u² + (???)u + (???) = 0 很抱歉，手动完成这个过程非常繁琐，而且容易出错。我没有工具来完成这项任务，也不使用Python，因此您正在使用的数学库对我来说是未知的。但是，它应该能够帮助您找到如何计算 (???)u² + (???)u + (???) = 0 的系数。

更新

忽略上面的大部分，因为我犯了一个错误。 b - (a + c) == 0 不等同于 b² - (a² + c²) == 0。第一个是需要的，这在处理根式时是一个问题（请注意，仍然可以使用 a + bi == sqrt(a^2 + b^2) 的解决方案，其中 i 是虚数）。

另一种解决方案

所以我探索了其他选项。

最简单的有一个小缺陷。它将返回拦截的时间。但必须验证它，因为它还将返回拦截线而不是线段BC的时间

因此，当找到结果时，您需要通过将找到的点和线段的点积除以线段长度的平方来测试它。请参见测试片段中的 isPointOnLine 函数。

为了解决问题，我使用以下事实：线段BC的叉积和从B到A的向量在点在直线上时为0。

一些重命名

使用上面的图像，我重新命名变量，以便更容易地进行所有琐碎的部分。

/*
point P is  {a,b}
point L1 is  {c,d}
point L2 is  {e,f}
vector V1 is {g,h}
vector V2 is {i,j}
vector V3 is {k,l}

Thus for points A,B,C over time u    */
Ax = (a+g*u)
Ay = (b+h*u)
Bx = (c+i*u)
By = (d+j*u)
Cx = (e+k*u)
Cy = (f+l*u)

/* Vectors BA and BC at u */
Vbax = ((a+g*u)-(c+i*u))
Vbay = ((b+h*u)-(d+j*u))
Vbcx = ((e+k*u)-(c+i*u))
Vbcy = ((f+l*u)-(d+j*u))

/*
   thus Vbax * Vbcy - Vbay * Vbcx == 0 at intercept 
*/

这将给出二次方程。

0 = ((a+g*u)-(c+i*u)) * ((f+l*u)-(d+j*u)) - ((b+h*u)-(d+j*u)) * ((e+k*u)-(c+i*u))

重新排列后我们得到

0 = -((i*l)-(h*k)+g*l+i*h+(i+k)*j-(g+i)*j)*u* u -(d*g-c*l-k*b-h*e+l*a+g*f+i*b+c*h+(i+k)*d+(c+e)*j-((f+d)*i)-((a+c)*j))*u +(c+e)*d-((a+c)*d)+a*f-(c*f)-(b*e)+c*b

系数因此为：

 A = -((i*l)-(h*k)+g*l+i*h+(i+k)*j-(g+i)*j)
 B = -(d*g-c*l-k*b-h*e+l*a+g*f+i*b+c*h+(i+k)*d+(c+e)*j-((f+d)*i)-((a+c)*j))
 C = (c+e)*d-((a+c)*d)+a*f-(c*f)-(b*e)+c*b

我们可以使用二次公式来解决问题（见右上方图像）。

请注意，可能会有两个解。在这个例子中，我忽略了第二个解。然而，由于第一个解可能不在线段上，所以如果第一个解失败，您需要保留第二个解，但只有在范围0 <= u <= 1内时才有效。您还需要验证该结果。

测试

为了避免错误，我必须对解决方案进行测试。

下面是一个生成随机线对并生成随机线直到找到拦截的片段的代码段。

相关函数包括：

• movingLineVPoint，如果有，则返回第一个拦截的单位时间。
• isPointOnLine，用于验证结果。

const ctx = canvas.getContext("2d");
canvas.addEventListener("click",test);
const W = 256, H = W, D = (W ** 2 * 2) ** 0.5;
canvas.width  = W; canvas.height = H;
const rand = (m, M) => Math.random() * (M - m) + m;
const Tests = 300;
var line1, line2, path, count = 0; 
setTimeout(test, 0);

// creating P point L line
const P = (x,y) => ({x,y,get arr() {return [this.x, this.y]}}); 
const L = (l1, l2) => ({l1,l2,vec: P(l2.x - l1.x, l2.y - l1.y), get arr() {return [this.l1, this.l2]}}); 
const randLine = () => L(P(rand(0, W), rand(0, H)), P(rand(0, W), rand(0, H)));
const isPointOnLine = (p, l) =>  {
    const x = p.x - l.l1.x;
    const y = p.y - l.l1.y;
    const u = (l.vec.x * x + l.vec.y * y) / (l.vec.x * l.vec.x + l.vec.y * l.vec.y);
    return u >= 0 && u <= 1;
}
// See answer illustration for names
// arguments in order Px,Py,L1x,l1y,l2x,l2y,V1x,V1y,V2x,V2y,V3x,V3y
function movingLineVPoint(a,b, c,d, e,f, g,h, i,j, k,l) {
    var A = -(i*l)-(h*k)+g*l+i*h+(i+k)*j-(g+i)*j;
    var B = -d*g-c*l-k*b-h*e+l*a+g*f+i*b+c*h+(i+k)*d+(c+e)*j-((f+d)*i)-((a+c)*j)
    var C = +(c+e)*d-((a+c)*d)+a*f-(c*f)-(b*e)+c*b

    // Find roots if any. Could be up to 2
    // Using the smallest root >= 0 and <= 1
    var u, D, u1, u2;
    // if A is tiny we can ignore
    if (Math.abs(A) < 1e-6) { 
        if (B !== 0) {
            u = -C / B;
            if (u < 0 || u > 1) { return }  // !!!!  no solution  !!!!
        } else { return }                   // !!!!  no solution  !!!!
    } else {
        B /= A;
        D = B * B - 4 * (C / A);
        if (D > 0) {
            D **= 0.5;
            u1 = 0.5 * (-B + D);
            u2 = 0.5 * (-B - D);
            if ((u1 < 0 || u1 > 1) && (u2 < 0 || u2 > 1))  { return }  // !!!!  no solution  !!!!
            if (u1 < 0 || u1 > 1) { u = u2 }        // is first out of range
            else if (u2 < 0 || u2 > 1) { u = u1 }   // is second out of range
            else if (u1 < u2) { u = u1 }            // first is smallest
            else { u = u2 }
        } else if (D === 0) {
            u = 0.5 * -B;
            if (u < 0 || u > 1)  { return }  // !!!!  no solution  !!!!            
        } else { return }                    // !!!!  no solution  !!!! 
    }    
    return u;
}

function test() {
   if (count> 0) { return }
   line1 = randLine();
   line2 = randLine();
   count = Tests
   subTest();
}
function subTest() {
   path = randLine()
   ctx.clearRect(0,0,W,H);
   drawLines();
   const u = movingLineVPoint(
       path.l1.x, path.l1.y,
       line1.l1.x, line1.l1.y,
       line2.l1.x, line2.l1.y,
       path.vec.x, path.vec.y,
       line1.vec.x, line1.vec.y,
       line2.vec.x, line2.vec.y
   );
   
   if (u !== undefined) { // intercept found maybe
      pointAt = P(path.l1.x + path.vec.x * u, path.l1.y + path.vec.y * u);
      lineAt = L(
          P(line1.l1.x + line1.vec.x * u, line1.l1.y + line1.vec.y * u),
          P(line2.l1.x + line2.vec.x * u, line2.l1.y + line2.vec.y * u)
      );
      const isOn = isPointOnLine(pointAt, lineAt);
      if (isOn) {
          drawResult(pointAt, lineAt);
          count = 0;
          info.textContent = "Found at: u= " + u.toFixed(4) + ". Click for another";
          return;
      }
   }
   setTimeout((--count < 0 ? test : subTest), 18);
}   








function drawLine(line, col = "#000", lw = 1) {
    ctx.lineWidth = lw;
    ctx.strokeStyle = col;
    ctx.beginPath();
    ctx.lineTo(...line.l1.arr);
    ctx.lineTo(...line.l2.arr);
    ctx.stroke();
}
function markPoint(p, size = 3, col = "#000", lw = 1) {
    ctx.lineWidth = lw;
    ctx.strokeStyle = col;
    ctx.beginPath();
    ctx.arc(...p.arr, size, 0, Math.PI * 2);
    ctx.stroke();
}
function drawLines() {
   drawLine(line1);
   drawLine(line2);
   markPoint(line1.l1);
   markPoint(line2.l1);
   drawLine(path, "#0B0", 1);
   markPoint(path.l1, 2, "#0B0", 2);
}
function drawResult(pointAt, lineAt) {
   ctx.clearRect(0,0,W,H);
   drawLines();
   markPoint(lineAt.l1, 2, "red", 1.5);
   markPoint(lineAt.l2, 2, "red", 1.5);
   markPoint(pointAt, 2, "blue", 3);
   drawLine(lineAt, "#BA0", 2);
}

div {position: absolute; top: 10px; left: 12px}
canvas {border: 2px solid black}

<canvas id="canvas" width="1024" height="1024"></canvas>
    <div><span id="info">Click to start</span></div>

- Blindman67

---

我认为这种方法非常优雅，因为它消除了在 OP 的方法中处理段落位置（a）的需要。只需要解决时间（t，或这里的 u），我认为这很整洁。很快就会尝试。我投了赞成票，但由于声望不够，它并没有显示出来。 - PawelBoe

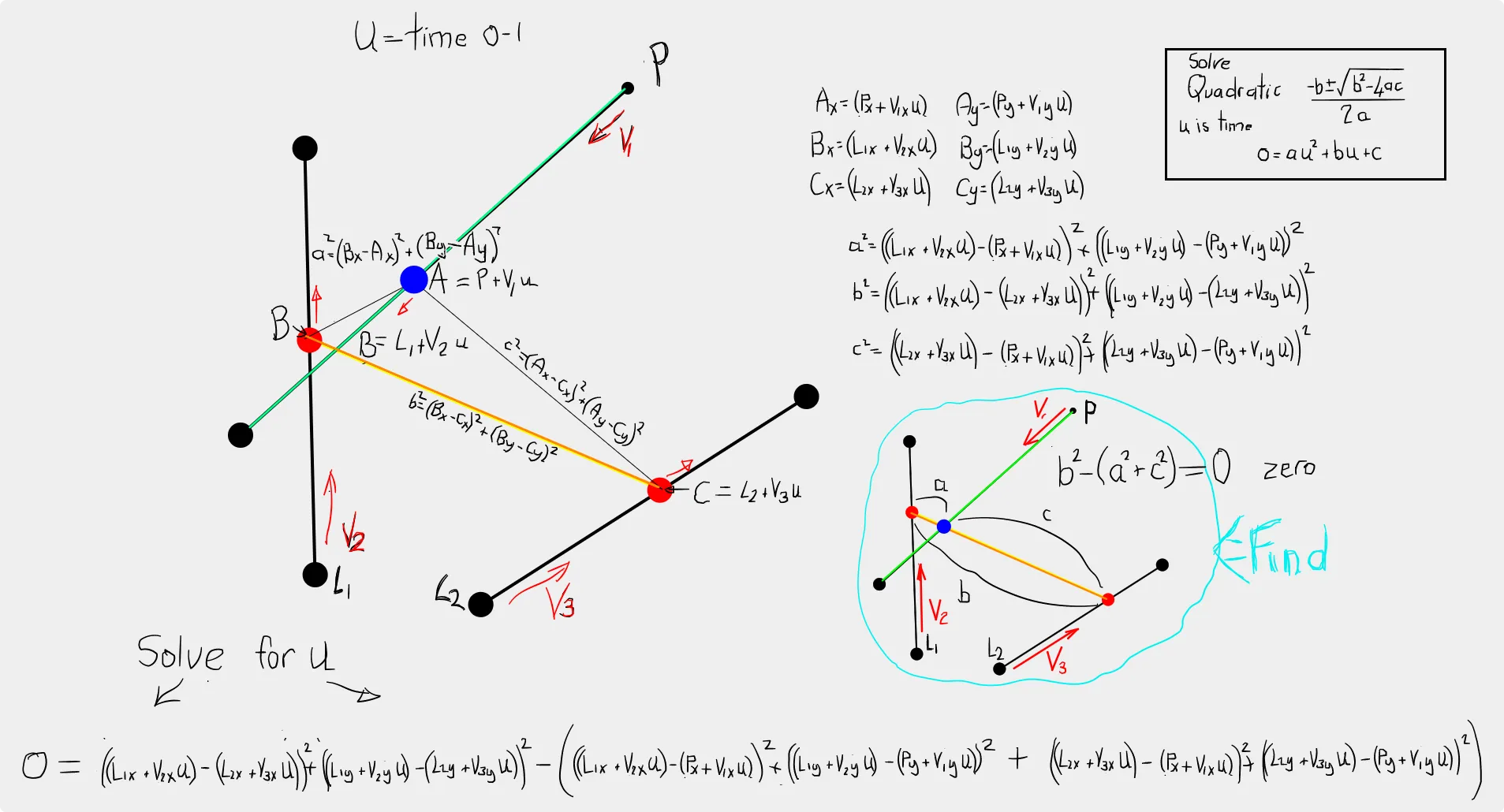
@PawelBoe 我再次查看了我的答案，发现有一个错误。我将线段长度a、b、c保留为长度的平方。这是不正确的。它们需要是长度，即 b^2 - (a^2+c^2) == 0 应该是 b- (a+c) == 0 对此我感到非常抱歉 :( - Blindman67

@PawelBoe 哦，这意味着系数不能被表述。作为答案的话这是不行的。 - Blindman67

但是最后一种方法和解释确实非常有帮助！非常感谢。我自己验证了重新排列，得到了略微不同（但等效）的系数表示，但这没关系。 我想知道在某些边缘情况下会发生什么，比如当线段静止时（两个边缘的运动向量为（0,0）），但点沿着线段移动时会发生什么

• 这不应该导致无限解吗？就目前而言，对我来说还可以。

- PawelBoe

@PawelBoe 如果一个问题可以表示为单个值（在这种情况下是时间），并且函数小于5次多项式，则此方法非常有效。我要指出的是，对于您的问题，如果您将整个问题缩放和旋转，使L1位于原点（0,0），并且V2是沿x轴的单位向量，则可以删除许多术语。例如，第二个prob coefs变成类似于A = -l-(h*k)+g*l+h; B = -k*b-h*e+l*a+g*f+b-f-a; C = a*f-b*e，因为c = d = j = 0 & i = 1。如果您正在重复问题的某些部分，则效果很好。例如，1条移动线和许多移动点。 - Blindman67

Answer 2

我不理解@Blindman67的解决方案中的两个部分：

• 解决 b^2 - (a^2 + c^2) = 0 而不是 sqrt(b^2)-(sqrt(a^2)+sqrt(b^2)) = 0
• 返回的时间戳被夹在范围 [0,1] 内

也许我错过了一些显而易见的东西，但无论如何，我设计了一个解决这些问题的解决方案：

• 解决所有二次项，而不仅仅是一个
• 返回的时间戳没有限制
• 解决 sqrt(b^2)-(sqrt(a^2)+sqrt(b^2)) = 0 而不是 b^2 - (a^2 + c^2) = 0

欢迎推荐优化方法：

# pnt, crt_1, and crt_2 are points, each with x,y and dx,dy attributes
# returns a list of timestamps for which pnt is on the segment
# whose endpoints are crt_1 and crt_2
def colinear_points_collision(pnt, crt_1, crt_2):
    a, b, c, d = pnt.x, pnt.y, pnt.dx, pnt.dy
    e, f, g, h = crt_1.x, crt_1.y, crt_1.dx, crt_1.dy
    i, j, k, l = crt_2.x, crt_2.y, crt_2.dx, crt_2.dy

    m = a - e
    n = c - g
    o = b - f
    p = d - h
    q = a - i
    r = c - k
    s = b - j
    u = d - l
    v = e - i
    w = g - k
    x = f - j
    y = h - l

    # Left-hand expansion
    r1 = n * n + p * p
    r2 = 2 * o * p + 2 * m * n
    r3 = m * m + o * o
    r4 = r * r + u * u
    r5 = 2 * q * r + 2 * s * u
    r6 = q * q + s * s

    coef_a = 4 * r1 * r4  # t^4 coefficient
    coef_b = 4 * (r1 * r5 + r2 * r4)  # t^3 coefficient
    coef_c = 4 * (r1 * r6 + r2 * r5 + r3 * r4)  # t^2 coefficient
    coef_d = 4 * (r2 * r6 + r3 * r5)  # t coefficient
    coef_e = 4 * r3 * r6  # constant

    # Right-hand expansion
    q1 = (w * w + y * y - n * n - p * p - r * r - u * u)
    q2 = 2 * (v * w + x * y - m * n - o * p - q * r - s * u)
    q3 = v * v + x * x - m * m - o * o - q * q - s * s

    coef1 = q1 * q1  # t^4 coefficient
    coef2 = 2 * q1 * q2  # t^3 coefficient
    coef3 = 2 * q1 * q3 + q2 * q2  # t^2 coefficient
    coef4 = 2 * q2 * q3  # t coefficient
    coef5 = q3 * q3  # constant

    # Moves all the coefficients onto one side of the equation to get
    # at^4 + bt^3 + ct^2 + dt + e
    # solve for possible values of t
    p = np.array([coef1 - coef_a, coef2 - coef_b, coef3 - coef_c, coef4 - coef_d, coef5 - coef_e])

    def fun(x):
        return p[0] * x**4 + p[1] * x**3 + p[2] * x**2 + p[3] * x + p[4]

    # could use np.root, but I found this to be more numerically stable
    sol = optimize.root(fun, [0, 0], tol=0.002)
    r = sol.x

    uniques = np.unique(np.round(np.real(r[np.isreal(r)]), 4))
    final = []

    for r in uniques[uniques > 0]:
        if point_between(e + g * r, f + h * r, i + k * r, j + l * r, a + c * r, b + d * r):
            final.append(r)

    return np.array(final)

# Returns true if the point (px,py) is between the endpoints
# of the line segment whose endpoints lay at (ax,ay) and (bx,by)
def point_between(ax, ay, bx, by, px, py):
    # colinear already checked above, this checks between the other two.
    return (min(ax, bx) <= px <= max(ax, bx) or abs(ax - bx) < 0.001) and (min(ay, by) <= py <= max(ay, by) or abs(ay - by) < 0.001)

一个例子（L1和L2是线段的端点）：
P = (0,0) 速度为 (0, +1)
L1 = (-1,2) 速度为 (0, -1)
L2 = (1,2) 速度为 (0, -1)

返回结果应该是 t=1，因为经过1个时间步长后，P将向上移动一个单位，而线段的两个端点将各向下移动一个单位，因此，该点在t=1时与线段相交。

- widavies