理论上,法向量并不是真正的向量,它们最好被视为bivectors,只是在三维空间中向量和双线性形式都有三个分量,因此将它们识别为相同的。如果我们生活在一个四维世界中,我们就不会有这种困惑。在那里,向量将有4个分量,而双线性形式则有6个分量。
双线性形式和pseudovectors /轴向量之间存在微妙的区别。如果 i、j、k 是向量的基元素,则双线性形式具有基础 j ^ k、i ^ k 和 i ^ j,Hodge双线性映射一个集合到另一个集合,并将双线性形式映射到伪向量。双线性形式可以始终被视为两个其他向量的叉积。
如果您认为法向量总是由一些切向量对的叉积得出的,那么您可以通过首先转换这两个切向量然后取它们的叉积来找到法向量的变换。
让我们将问题中的图表想象成通过圆柱体的切片。在第一张图片中,当横截面为圆形时,两个切向量分别为
(1/rt2, 1/rt2, 0)和
(0,0,1),其中rt2 = sqrt(2)。取叉积得到:
( 1/rt2 ) ( 0 ) ( 1/rt2 )
( 1/rt2 ) X ( 0 ) = ( -1/rt2 )
( 0 ) ( 1 ) ( 0 )
现在进行一个挤压操作 (x,y,z) -> (x, y/2, z),切向量会转变为 (1/rt2, 1/(2 rt2), 0) 和 (0,0,1)。取叉积。
( 1/rt2 ) ( 0 ) ( 1/(2 rt2) )
( 1/(2 rt2) ) X ( 0 ) = ( -1/rt2 )
( 0 ) ( 1 ) ( 0 )
将其标准化后得到(1/√5,-2/√5,0)。
选择哪一对切向量并不重要,我们仍然会得到相同的结果。上面的计算有点冗长,需要找到一对合适的切向量。使用转置的逆矩阵更简单。
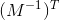 进行转换。
进行转换。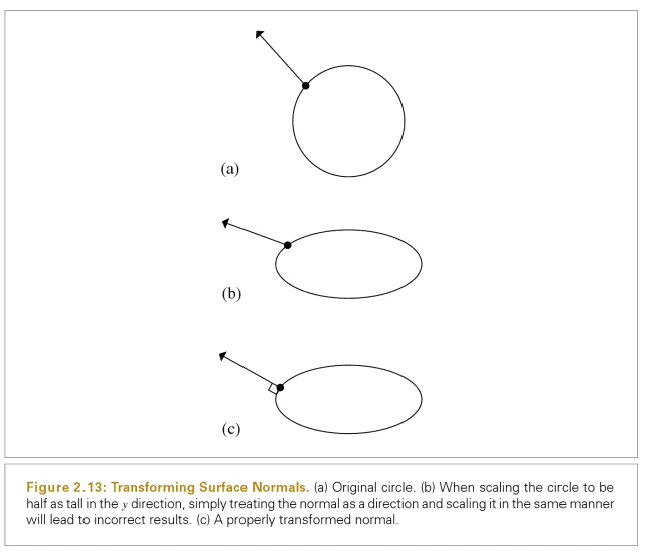 我曾读到过这样的法线变换需要保持法线和切线的正交性。但我想得到一些直观的解释。
我曾读到过这样的法线变换需要保持法线和切线的正交性。但我想得到一些直观的解释。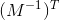 进行转换。
进行转换。 我曾读到过这样的法线变换需要保持法线和切线的正交性。但我想得到一些直观的解释。
我曾读到过这样的法线变换需要保持法线和切线的正交性。但我想得到一些直观的解释。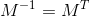 。这意味着
。这意味着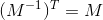 ,因此对于这些类型的变换,处理并没有什么特殊之处。
,因此对于这些类型的变换,处理并没有什么特殊之处。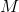 来转换法线是不够的,需要使用
来转换法线是不够的,需要使用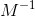 来转换法线,在对称情况下等于
来转换法线,在对称情况下等于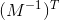 。
。