在 R 中进行指数曲线拟合
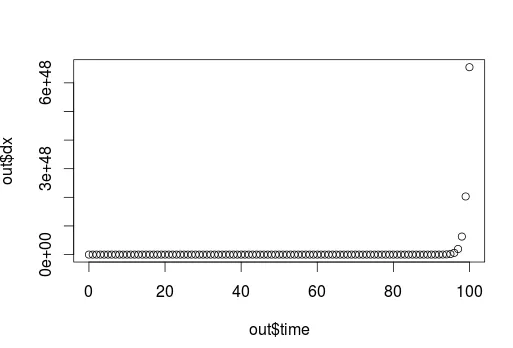
20
- Si22
1
你能发布 “y” 吗?你需要假设一个模型,然后说“这是一个指数曲线”。或者你可以使用样条函数而不需要模型。 - Colonel Beauvel
3个回答
41
你需要一个模型来适应数据。
不知道你的模型的全部细节,假设这是一个指数增长模型,可以写成:y = a * e r*t
其中y是您的测量变量,t是测量时的时间,a是当t = 0时y的值,r是增长常数。我们想要估计a和r。
这是一个非线性问题,因为我们想要估计指数r。然而,在这种情况下,我们可以使用一些代数方法,并通过在两侧取对数并解决(记住对数规则)将其转化为线性方程,结果为:log(y) = log(a) + r * t。
我们可以通过一个例子来进行可视化,从我们的模型中生成曲线,假设一些值为a和r:
让我们通过一些包含添加噪声的模拟来说明(从正态分布中采样),以模拟真实数据。请参阅StackExchange post以了解此模拟背后的推理(由Alejo Bernardin's comment指出)。
使用
通过绘制模型的残差,您可以看到误差方差在数据范围内是合理恒定的:
针对乘性误差情况(我们的
为了解释这个输出,需要再次记住我们的线性化模型是log(y) = log(a) + r*t,等价于一个形式为Y = β0 + β1 * X的线性模型,其中β0是截距,β1是斜率。
因此,在这个输出中,
值得注意的是,如果我们使用
现在我们高估了a并低估了r(Mario Reutter在他的评论中强调了这一点)。我们可以想象使用错误的方法来拟合我们的模型的后果:
您可以再次绘制此模型的残差图,以查看数据范围内方差不是恒定的(我们也可以在上面的图表中看到这一点,其中数据的扩散随着 t 值的增加而增加)。
这是一个非线性问题,因为我们想要估计指数r。然而,在这种情况下,我们可以使用一些代数方法,并通过在两侧取对数并解决(记住对数规则)将其转化为线性方程,结果为:log(y) = log(a) + r * t。
我们可以通过一个例子来进行可视化,从我们的模型中生成曲线,假设一些值为a和r:
t <- 1:100 # these are your time points
a <- 10 # assume the size at t = 0 is 10
r <- 0.1 # assume a growth constant
y <- a*exp(r*t) # generate some y observations from our exponential model
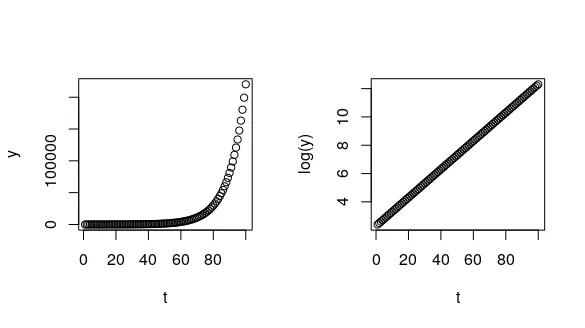
# visualise
par(mfrow = c(1, 2))
plot(t, y) # on the original scale
plot(t, log(y)) # taking the log(y)
- 将我们的非线性模型拟合到原始数据上(例如使用
nls()函数) - 将我们的“线性化”模型拟合到对数转换后的数据上(例如使用
lm()函数)
让我们通过一些包含添加噪声的模拟来说明(从正态分布中采样),以模拟真实数据。请参阅StackExchange post以了解此模拟背后的推理(由Alejo Bernardin's comment指出)。
set.seed(12) # for reproducible results
# errors constant across time - additive
y_add <- a*exp(r*t) + rnorm(length(t), sd = 5000) # or: rnorm(length(t), mean = a*exp(r*t), sd = 5000)
# errors grow as y grows - multiplicative (constant on the log-scale)
y_mult <- a*exp(r*t + rnorm(length(t), sd = 1)) # or: rlnorm(length(t), mean = log(a) + r*t, sd = 1)
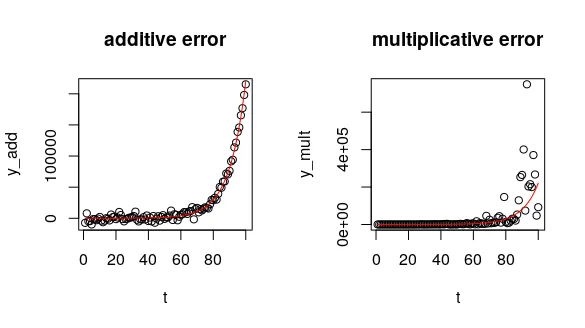
# visualise
par(mfrow = c(1, 2))
plot(t, y_add, main = "additive error")
lines(t, a*exp(t*r), col = "red")
plot(t, y_mult, main = "multiplicative error")
lines(t, a*exp(t*r), col = "red")
nls(),因为误差在t上是恒定的。使用nls()时,我们需要指定一些优化算法的起始值(尽量“猜测”这些值,因为nls()经常难以收敛到一个解决方案)。add_nls <- nls(y_add ~ a*exp(r*t),
start = list(a = 0.5, r = 0.2))
coef(add_nls)
# a r
# 11.30876845 0.09867135
使用
coef()函数,我们可以获得两个参数的估计值。这给了我们不错的估计值,接近于我们模拟的结果(a = 10和r = 0.1)。通过绘制模型的残差,您可以看到误差方差在数据范围内是合理恒定的:
plot(t, resid(add_nls))
abline(h = 0, lty = 2)
针对乘性误差情况(我们的
y_mult 模拟值),我们应该在对数转换后的数据上使用 lm(),因为在该尺度上误差是恒定的。mult_lm <- lm(log(y_mult) ~ t)
coef(mult_lm)
# (Intercept) t
# 2.39448488 0.09837215
为了解释这个输出,需要再次记住我们的线性化模型是log(y) = log(a) + r*t,等价于一个形式为Y = β0 + β1 * X的线性模型,其中β0是截距,β1是斜率。
因此,在这个输出中,
(Intercept)相当于我们模型中的log(a),而t是时间变量的系数,等价于我们的r。
要有意义地解释(Intercept),我们可以取它的指数(exp(2.39448488)),得到约10.96,这非常接近我们的模拟值。值得注意的是,如果我们使用
nls函数拟合误差是乘法的数据,会发生什么:mult_nls <- nls(y_mult ~ a*exp(r*t), start = list(a = 0.5, r = 0.2))
coef(mult_nls)
# a r
# 281.06913343 0.06955642
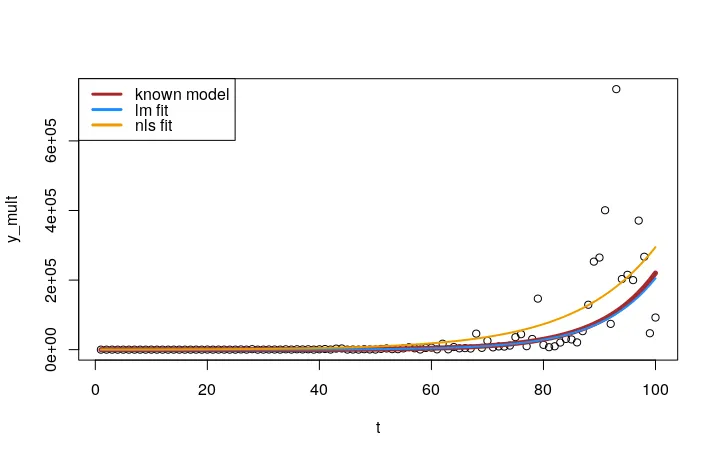
现在我们高估了a并低估了r(Mario Reutter在他的评论中强调了这一点)。我们可以想象使用错误的方法来拟合我们的模型的后果:
# get the model's coefficients
lm_coef <- coef(mult_lm)
nls_coef <- coef(mult_nls)
# make the plot
plot(t, y_mult)
lines(t, a*exp(r*t), col = "brown", lwd = 5)
lines(t, exp(lm_coef[1])*exp(lm_coef[2]*t), col = "dodgerblue", lwd = 2)
lines(t, nls_coef[1]*exp(nls_coef[2]*t), col = "orange2", lwd = 2)
legend("topleft", col = c("brown", "dodgerblue", "orange2"),
legend = c("known model", "nls fit", "lm fit"), lwd = 3)
lm() 拟合要比对原始数据使用 nls() 拟合好得多。您可以再次绘制此模型的残差图,以查看数据范围内方差不是恒定的(我们也可以在上面的图表中看到这一点,其中数据的扩散随着 t 值的增加而增加)。
plot(t, resid(mult_nls))
abline(h = 0, lty = 2)
- hugot
3
3如果有人想了解何时使用
lm()或nls(),这里有一个很好的讨论https://stats.stackexchange.com/questions/61747/linear-vs-nonlinear-regression?rq=1 - Alejo Bernardin1将对数值进行线性模型拟合(使用
lm)与拟合非线性模型(使用nls)得到的结果不同,因为最小化的距离不同。对于对数化的线性模型,对数化的残差被最小化,从而产生了偏差,使得剩余较大的残差偏离。因此,增长的开始更容易被错误地估计。 - Mario Reutter3@wpkzz 是的,原先的回答在根本上是错误的。我已经完全重写了它,希望现在准确无误。感谢您指出这个问题(五年后回来看到这个问题真是有些自惭形秽……) - hugot
5
很遗憾,取对数并拟合线性模型不是最优解。原因是,当将指数函数应用于返回原始模型时,大y值的误差的权重要比小y值的误差更大。以下是一个例子:
f <- function(x){exp(0.3*x+5)}
squaredError <- function(a,b,x,y) {sum((exp(a*x+b)-f(x))^2)}
x <- 0:12
y <- f(x) * ( 1 + sample(-300:300,length(x),replace=TRUE)/10000 )
x
y
#--------------------------------------------------------------------
M <- lm(log(y)~x)
a <- unlist(M[1])[2]
b <- unlist(M[1])[1]
print(c(a,b))
squaredError(a,b,x,y)
approxPartAbl_a <- (squaredError(a+1e-8,b,x,y) - squaredError(a,b,x,y))/1e-8
for ( i in 0:10 )
{
eps <- -i*sign(approxPartAbl_a)*1e-5
print(c(eps,squaredError(a+eps,b,x,y)))
}
结果:
> f <- function(x){exp(0.3*x+5)}
> squaredError <- function(a,b,x,y) {sum((exp(a*x+b)-f(x))^2)}
> x <- 0:12
> y <- f(x) * ( 1 + sample(-300:300,length(x),replace=TRUE)/10000 )
> x
[1] 0 1 2 3 4 5 6 7 8 9 10 11 12
> y
[1] 151.2182 203.4020 278.3769 366.8992 503.5895 682.4353 880.1597 1186.5158 1630.9129 2238.1607 3035.8076 4094.6925 5559.3036
> #--------------------------------------------------------------------
>
> M <- lm(log(y)~x)
> a <- unlist(M[1])[2]
> b <- unlist(M[1])[1]
> print(c(a,b))
coefficients.x coefficients.(Intercept)
0.2995808 5.0135529
> squaredError(a,b,x,y)
[1] 5409.752
> approxPartAbl_a <- (squaredError(a+1e-8,b,x,y) - squaredError(a,b,x,y))/1e-8
> for ( i in 0:10 )
+ {
+ eps <- -i*sign(approxPartAbl_a)*1e-5
+ print(c(eps,squaredError(a+eps,b,x,y)))
+ }
[1] 0.000 5409.752
[1] -0.00001 5282.91927
[1] -0.00002 5157.68422
[1] -0.00003 5034.04589
[1] -0.00004 4912.00375
[1] -0.00005 4791.55728
[1] -0.00006 4672.70592
[1] -0.00007 4555.44917
[1] -0.00008 4439.78647
[1] -0.00009 4325.71730
[1] -0.0001 4213.2411
>
也许可以尝试一些数值方法,比如梯度搜索,来找到平方误差函数的最小值。
- mra68
1
一张图表会大大提升您的回答。 - Rodrigo
4
如果确实是指数关系,你可以尝试取对数,并将线性模型拟合到这个变量上。
- Adama
网页内容由stack overflow 提供, 点击上面的可以查看英文原文,
原文链接
原文链接