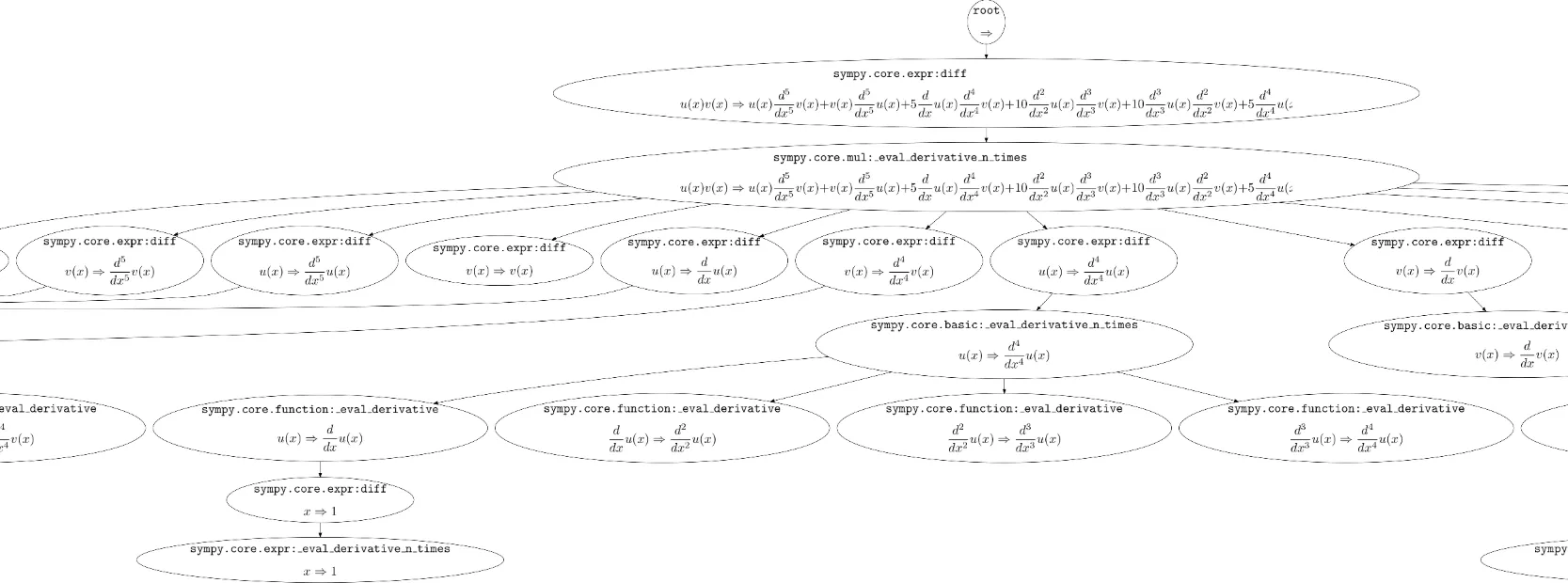
在我的研究中,我试图解决Kolmogorov反向方程,即对以下式子感兴趣: $$Af = b(x)f'(x)+\sigma(x)f''(x)$$
根据特定的b(x)和\sigma(x),我想看到在计算更高的Af幂时,表达式的系数增长速度有多快。我很难从分析上推导出这一点,因此尝试通过经验主义来观察趋势。
首先,我使用了sympy:
from sympy import *
import matplotlib.pyplot as plt
import re
import math
import numpy as np
import time
np.set_printoptions(suppress=True)
x = Symbol('x')
b = Function('b')(x)
g = Function('g')(x)
def new_coef(gamma, beta, coef_minus2, coef_minus1, coef):
return expand(simplify(gamma*coef_minus2 + beta*coef_minus1 + 2*gamma*coef_minus1.diff(x)\
+beta*coef.diff(x)+gamma*coef.diff(x,2)))
def new_coef_first(gamma, beta, coef):
return expand(simplify(beta*coef.diff(x)+gamma*coef.diff(x,2)))
def new_coef_second(gamma, beta, coef_minus1, coef):
return expand(simplify(beta*coef_minus1 + 2*gamma*coef_minus1.diff(x)\
+beta*coef.diff(x)+gamma*coef.diff(x,2)))
def new_coef_last(gamma, beta, coef_minus2):
return lambda x: gamma(x)*coef_minus2(x)
def new_coef_last(gamma, beta, coef_minus2):
return expand(simplify(gamma*coef_minus2 ))
def new_coef_second_to_last(gamma, beta, coef_minus2, coef_minus1):
return expand(simplify(gamma*coef_minus2 + beta*coef_minus1 + 2*gamma*coef_minus1.diff(x)))
def set_to_zero(expression):
expression = expression.subs(Derivative(b, x, x, x), 0)
expression = expression.subs(Derivative(b, x, x), 0)
expression = expression.subs(Derivative(g, x, x, x, x), 0)
expression = expression.subs(Derivative(g, x, x, x), 0)
return expression
def sum_of_coef(expression):
sum_of_coef = 0
for i in str(expression).split(' + '):
if i[0:1] == '(':
i = i[1:]
integers = re.findall(r'\b\d+\b', i)
if len(integers) > 0:
length_int = len(integers[0])
if i[0:length_int] == integers[0]:
sum_of_coef += int(integers[0])
else:
sum_of_coef += 1
else:
sum_of_coef += 1
return sum_of_coef
power = 6
charar = np.zeros((power, power*2), dtype=Symbol)
coef_sum_array = np.zeros((power, power*2))
charar[0,0] = b
charar[0,1] = g
coef_sum_array[0,0] = 1
coef_sum_array[0,1] = 1
for i in range(1, power):
#print(i)
for j in range(0, (i+1)*2):
#print(j, ':')
#start_time = time.time()
if j == 0:
charar[i,j] = set_to_zero(new_coef_first(g, b, charar[i-1, j]))
elif j == 1:
charar[i,j] = set_to_zero(new_coef_second(g, b, charar[i-1, j-1], charar[i-1, j]))
elif j == (i+1)*2-2:
charar[i,j] = set_to_zero(new_coef_second_to_last(g, b, charar[i-1, j-2], charar[i-1, j-1]))
elif j == (i+1)*2-1:
charar[i,j] = set_to_zero(new_coef_last(g, b, charar[i-1, j-2]))
else:
charar[i,j] = set_to_zero(new_coef(g, b, charar[i-1, j-2], charar[i-1, j-1], charar[i-1, j]))
#print("--- %s seconds for expression---" % (time.time() - start_time))
#start_time = time.time()
coef_sum_array[i,j] = sum_of_coef(charar[i,j])
#print("--- %s seconds for coeffiecients---" % (time.time() - start_time))
coef_sum_array
然后,研究了自动微分并使用了autograd:
import autograd.numpy as np
from autograd import grad
import time
np.set_printoptions(suppress=True)
b = lambda x: 1 + x
g = lambda x: 1 + x + x**2
def new_coef(gamma, beta, coef_minus2, coef_minus1, coef):
return lambda x: gamma(x)*coef_minus2(x) + beta(x)*coef_minus1(x) + 2*gamma(x)*grad(coef_minus1)(x)\
+beta(x)*grad(coef)(x)+gamma(x)*grad(grad(coef))(x)
def new_coef_first(gamma, beta, coef):
return lambda x: beta(x)*grad(coef)(x)+gamma(x)*grad(grad(coef))(x)
def new_coef_second(gamma, beta, coef_minus1, coef):
return lambda x: beta(x)*coef_minus1(x) + 2*gamma(x)*grad(coef_minus1)(x)\
+beta(x)*grad(coef)(x)+gamma(x)*grad(grad(coef))(x)
def new_coef_last(gamma, beta, coef_minus2):
return lambda x: gamma(x)*coef_minus2(x)
def new_coef_second_to_last(gamma, beta, coef_minus2, coef_minus1):
return lambda x: gamma(x)*coef_minus2(x) + beta(x)*coef_minus1(x) + 2*gamma(x)*grad(coef_minus1)(x)
power = 6
coef_sum_array = np.zeros((power, power*2))
coef_sum_array[0,0] = b(1.0)
coef_sum_array[0,1] = g(1.0)
charar = [b, g]
for i in range(1, power):
print(i)
charar_new = []
for j in range(0, (i+1)*2):
if j == 0:
new_funct = new_coef_first(g, b, charar[j])
elif j == 1:
new_funct = new_coef_second(g, b, charar[j-1], charar[j])
elif j == (i+1)*2-2:
new_funct = new_coef_second_to_last(g, b, charar[j-2], charar[j-1])
elif j == (i+1)*2-1:
new_funct = new_coef_last(g, b, charar[j-2])
else:
new_funct = new_coef(g, b, charar[j-2], charar[j-1], charar[j])
coef_sum_array[i,j] = new_funct(1.0)
charar_new.append(new_funct)
charar = charar_new
coef_sum_array
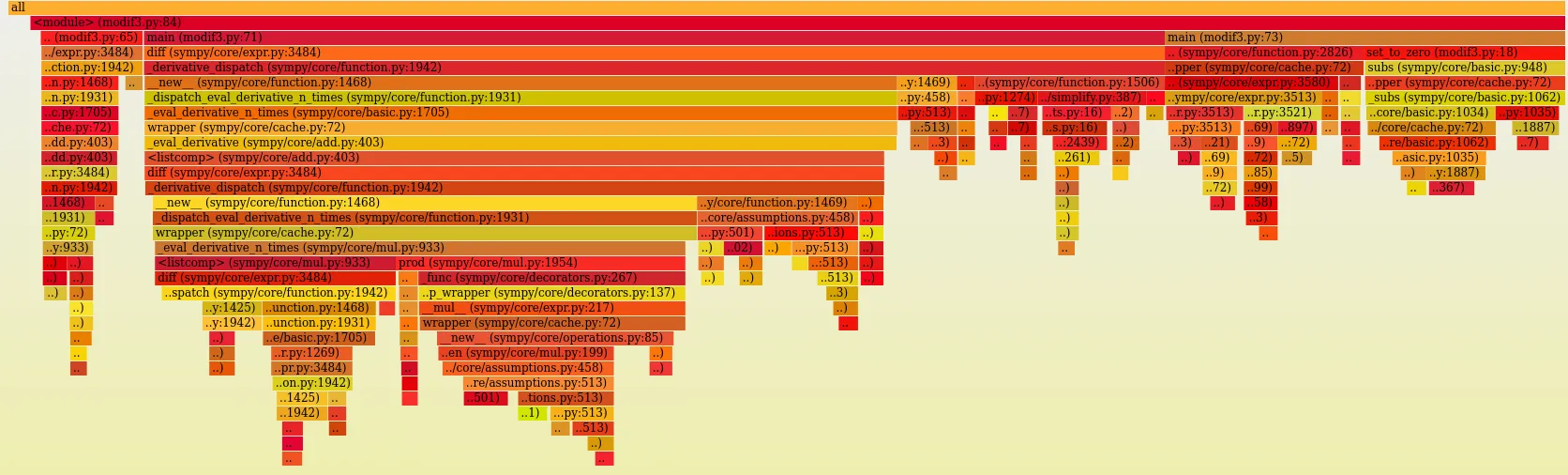
然而,我对它们的速度都不满意。在运行simpy方法3天后,我只得到了30个迭代,而我希望至少能做1000个迭代。
我期望第二种(数值)方法可以进行优化,以避免每次重新计算表达式。不幸的是,我自己没有看出解决方案。此外,我尝试过Maple,但也没有成功。
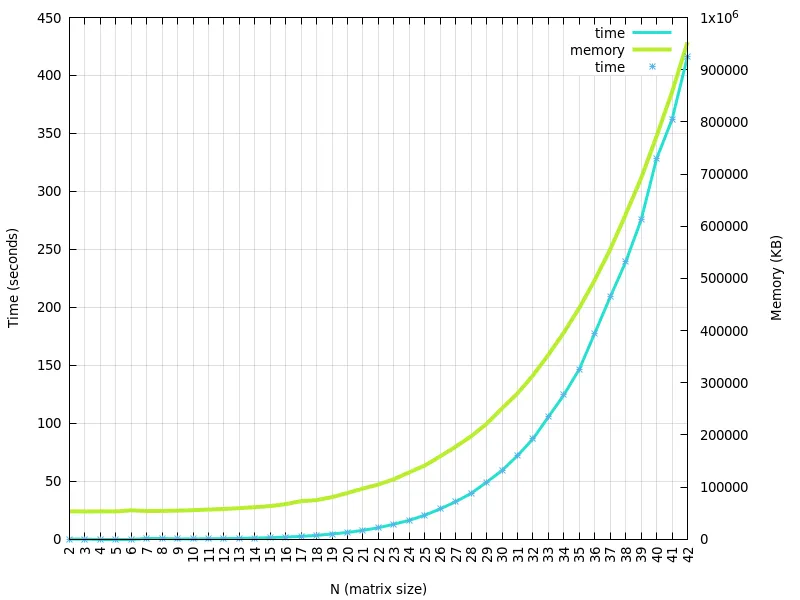
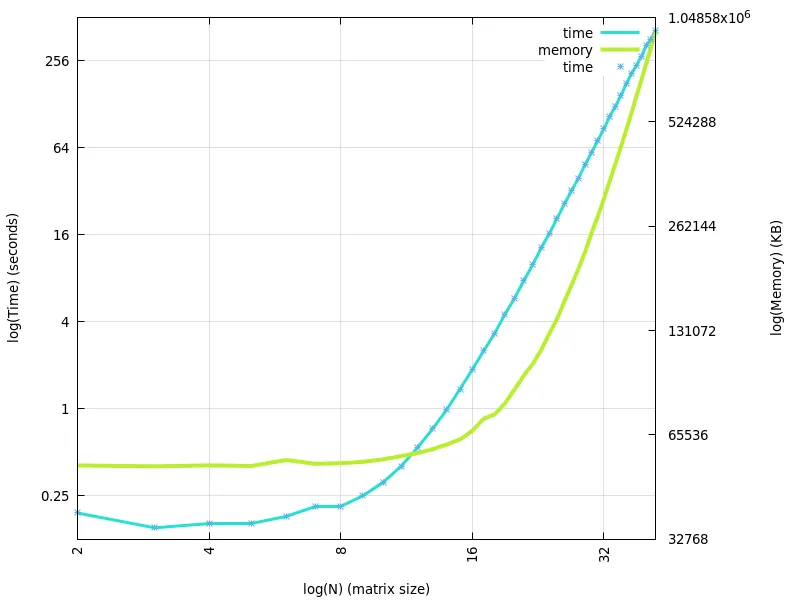
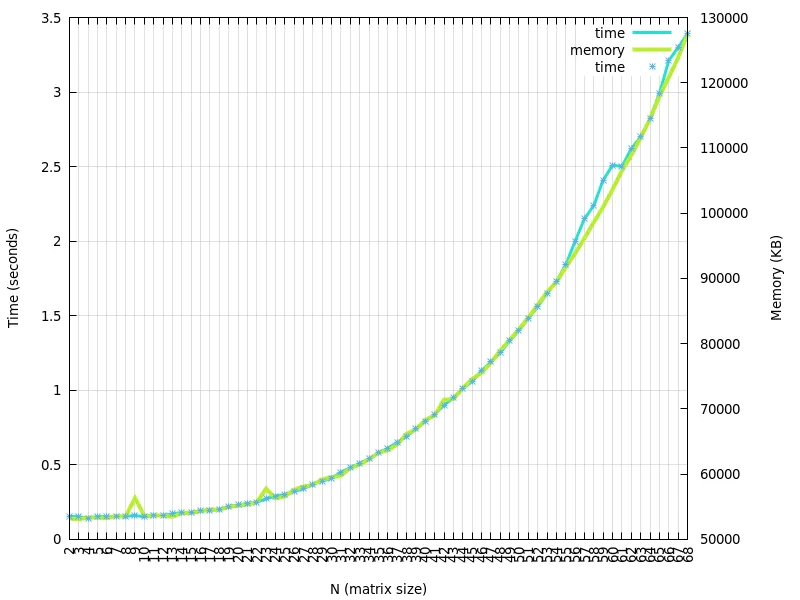
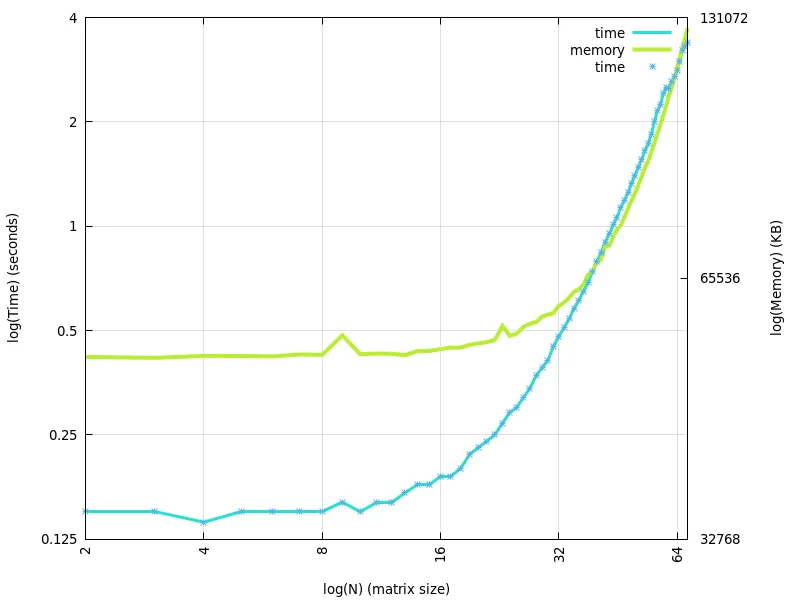
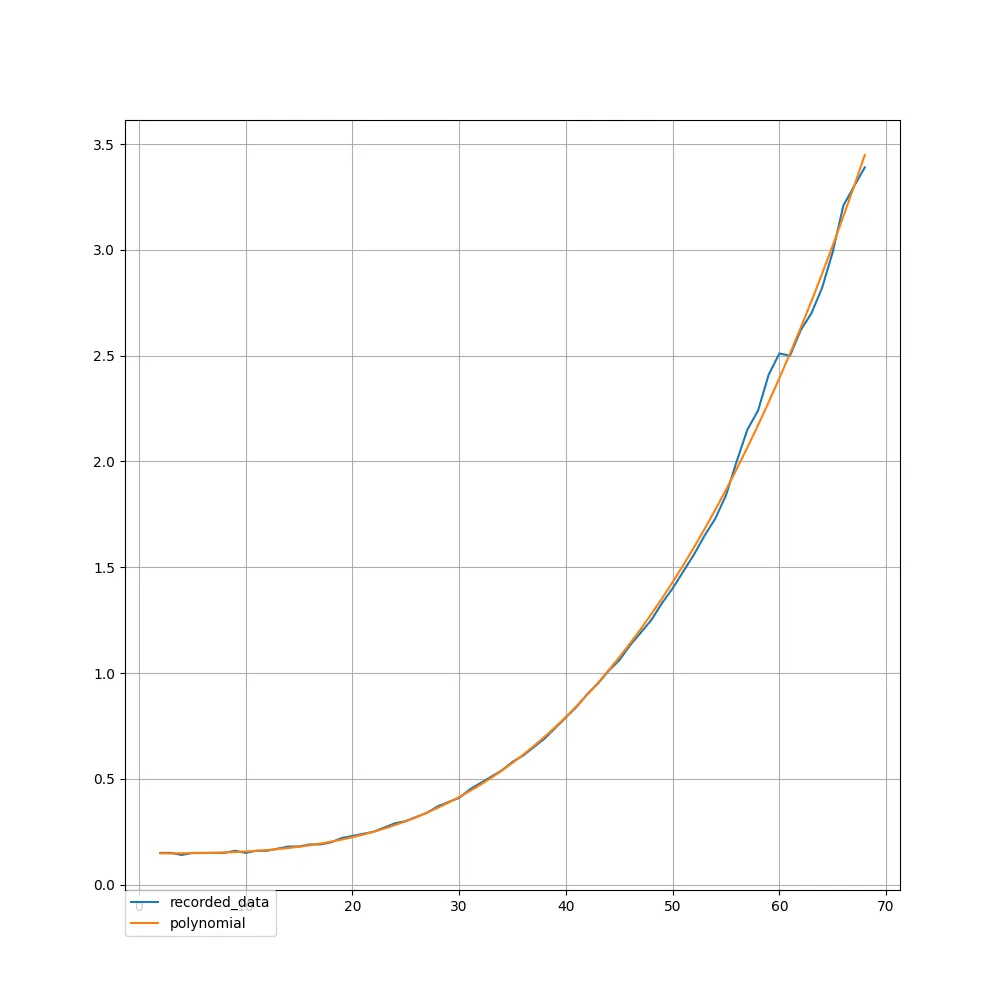
b=1+x和g=1+x+x**2来观察运行时间和内存使用情况。通常情况下,当使用符号方法太昂贵时(并且数值方法存在精度惩罚)才会使用数值方法。但是,如果您定义了函数b和g,则运行时间并不那么糟糕(请参见上文)。我认为这也很大程度上取决于您的实际b和g函数是什么。它们实际上是1+x和1+x+x**2还是其他东西? - wsdookadrb和g函数的前150个,我们仍然看到增长趋势。回答您的问题,目前仅需要处理1+x和1+x+x ** 2。而且在我看来,斜率计算是正确的 :) - Gabrielė Mongirdaitėvalues.append(sum(coef_sum_array[i]))values.insert(0, 2) answer = [] for i in range(1, power): answer.append(values[i - 1] / math.factorial(i)) plt.scatter(range(1, power), answer, marker='.', color='black') plt.show()`- Gabrielė Mongirdaitė