我希望确认一种方法，用于确定一个点是否位于三维空间中的三角形内。给定一个以R(t) = e + td形式表示的射线和由三个点T = {V0, V1, V2}构成的三角形集合，我知道如何找到这三个点所形成平面的参数方程，以及如何确定射线是否与该平面相交。最后，如果相交，我想知道交点是否实际上在三角形边界内。
请看下面的图片。
我的想法是，可以计算每条边向量与从第一条边向量指向该点的向量之间的点积，并检查它们是否全为正数。就像这样：
如果是这样，那么该点应该位于三角形内。对吗？这不是计算机图形学中用于确定背面的相同方法吗？
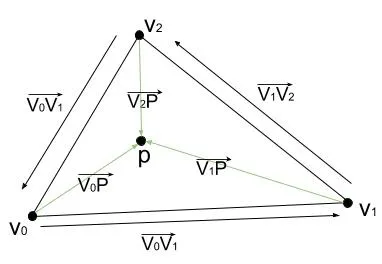
在图形学中，人们通常使用重心坐标系。在您的情况下，P 可以描述为 P = aV0 + bV1 + cV2，其中 a + b + c = 1。当且仅当 0 <= a, b, c <= 1 时，P 在三角形内。
如果由 v1、P、v2 组成的三角形的面积为 S1，由 P、v0、v2 组成的三角形的面积为 S2，并且 P、V0、V1 的面积为 S3。那么 a = S1/S，b = S2/S 和 c = S3/S，其中 S 是三角形 V0、V1、V2 的面积。
要找到 S = 1/2||(V0-V1)creosspdoruct(V0-V2)|| 的面积。
您可以查看我网站上发布的教程。
我有点晚到（抱歉），但是我对此有些看法：
我曾在80年代进行射线追踪。当时，我提出了一种与您讨论的相似的解决方案。
想法是，如果一个点始终位于三角形的边缘上逆时针行走的观察者右侧，那么该点就在三角形内部。
为此，我们需要测试是否每个边缘的右侧都存在该点。 叉积很好用，但是正如它所指出的那样，叉积会给你一个cos值。 您想要的是sin，因此可以拒绝具有负测试的点。 这就是人们倾向于使用叉积而不是点积的原因。 但是，叉积需要比点积更多的计算（在80年代这非常重要！）
但是我们可以通过简单的90度旋转将cos转换为sin！ 因此，我们不是计算点积而是在多边形平面中从边缘旋转90度的线计算它。
起初看起来很麻烦，但如果我们在主平面之一中工作，如XY、YZ或XZ，则不会。因此，让我们在其中一个主平面上以2D方式工作，而不是在三角形平面中以3D方式工作。如果一个点在3D中的多边形内部，它也将在其在2D平面上的投影内部。当然，如果多边形与其中一个主平面平行，如果我们在错误的平面上进行投影，可能会有问题。
因此，要选择这个平面，只需查看三角形的法线并选择更靠近三角形平面的平面。如果X分量最大，则使用YZ平面等等...此外，该分量的符号将告诉我们投影的多边形是顺时针��是逆时针。
在这些2D平面中，边的90度旋转只是交换值，并在其中一个值上改变符号。
例如，在XY平面上，V0和V1之间的边缘是：
V0V1x = v1x - v0x
V0V1y = V1y - v0y
V0和P之间的向量是：
V0Px = Px - V0x
V0Py = Py - V0y
将边旋转-90度，得到x' = y和y' = -x；
因此，我们计算第一条边的标量积为：
Scalar = (Px - V0x) * (V1y - V0y) + (Py - V0y) * (V0x - V1x)
如果该值小于0，则该点不在内部。
您可以使用另外两条边进行同样的操作，以完成“内部”测试。
在我的解决方案中，我预处理了一个值，用于给出每个三角形的最大法向量和符号。之后，我使用该值来确定要计算交点的平面。（负法向分量使我切换三角形的“顺时针”方向）。
检查点是否在多边形内部需要：
进行1个“方向”测试，最大正常值（一个有6种情况的开关，XY、XZ或YZ，正数或负数）
进行3个“边缘”测试，每个测试包括4次减法和2次乘法以及1个测试。
如果点在多边形内部，则只需进行3次“边缘”测试。否则，在第一次或第二次“边缘”测试后可能会被拒绝...
因此，知道一个点是否在三角形内需要8到22个操作。
我现在看到的大多数解决方案似乎使用的操作比这还要多！
E + t.D = a.V0 + b.V1 + c.V2
where
t, a, b, c >= 0, a + b + c = 1
使用c = 1 - a - b，您可以得到一个3x3线性系统（分解为x，y，z）
a.(V0 - V2) + b.(V1 - V2) - t.D = E - V2
如果你能解决t, a, b的问题，然后检查c是否为正数，那就太好了。
您可以使用点积来确定一个点是否在三角形内。首先找到测试点在每条边上的投影。点积的符号只有在直角时才有意义，而投影将给您一个直角。
对于三角形a、b、c和点p，计算每条边的m和s。m是点p在边ab上的投影点。
m = (p - a) • (b - a) / |b - a|² * (b - a) + a
s = (p - m) • (c - m)
s 是正数，则 p 和 c 在 ab 的同侧。对于每条边重复此测试。如果 p 和对面的顶点在每条边的同侧，则 p 在三角形内。|b - a|²，如果无法获得长度平方，则可以使用 (b - a) • (b - a)。