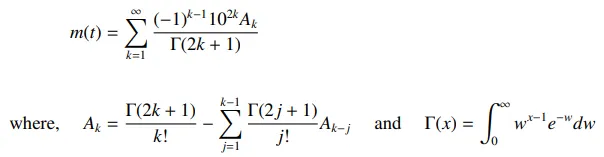威布尔分布的续航函数

Question

关于Weibull分布的更新函数 m(t)，其中t = 10的值如下所示。

我想找到m(t)的值。 我编写了以下的 r 代码来计算m(t)

last_term = NULL
gamma_k = NULL
n = 50
for(k in 1:n){
  gamma_k[k] = gamma(2*k + 1)/factorial(k)
}

for(j in 1: (n-1)){
  prev = gamma_k[n-j]
  last_term[j] = gamma(2*j + 1)/factorial(j)*prev
}

final_term = NULL
find_value = function(n){
  for(i in 2:n){
  final_term[i] = gamma_k[i] - sum(last_term[1:(i-1)])
  }
  return(final_term)
}
all_k = find_value(n)

af_sum = NULL
m_t = function(t){
for(k in 1:n){
af_sum[k] = (-1)^(k-1) * all_k[k] * t^(2*k)/gamma(2*k + 1)
}
  return(sum(na.omit(af_sum)))
}
m_t(20)

输出结果为m(t) = 2.670408e+93。我的迭代过程正确吗？谢谢。

- score324

---

我的建议是将问题分解成若干部分并逐一查看。首先尝试正确计算A[k]。手动计算几个项，如A[1]、A[2]、A[3]等，以便知道预期结果。然后尝试让程序计算A[k]以匹配预期结果。接下来，对于主求和式做类似的事情：通过手动计算前几个项，利用从A[k]中得到的知识，然后让程序匹配那些项。顺便说一句，如果求和式中的项不是很快地减少，那么对于任何少量的项，求和可能非常不准确。 - Robert Dodier

@score324 嗯，如果你喜欢它，你可以顶一下 - Severin Pappadeux

@score324 你只需要计算续订函数吗？如果是的话，使用库来完成这个任务是否可以？还是必须自己实现它？感谢提供信息。 - Robert Dodier

谢谢提供参考。以下是一些评论：（1）我看到你指定的m(t)实际上是针对t = 10和m = 2，其中m是Weibull形状参数。也许将方程中的t和m保留下来会帮助其他人理解。 （2）随着t和m的增加，求和变得更加困难。我不知道典型值是多少。您可以尝试确定典型值，并说明这些值以帮助其他人理解。 （3）此时可以尝试使用t^m的渐近逼近。 （4）您确定没有人在软件中实现了该函数吗？也许可以在面向统计的论坛上询问。 - Robert Dodier

顺便提一下，函数m(t)在范围0到4内的增长仅比线性略快 - 如果我正确实现了求和，则m(4)约为6.13。 - Robert Dodier

Answer 1

好的，所以我最终在这方面采用了一种非常不同的方法。我已经实现了一个简单的离散化积分方程，它定义了更新函数：

m(t) = F(t) + integrate (m(t - s)*f(s), s, 0, t)

使用矩形法近似计算积分。对不同的t值进行积分近似，得到一个线性方程组。我编写了一个函数来生成方程，并从中提取系数矩阵。在查看一些示例后，我猜测了一个规则来直接定义系数，并用它来生成一些示例的解。特别是像OP的例子一样尝试形状=2，t=10，步长为0.1（因此有101个方程）。

我发现结果与我在一篇论文中发现的近似结果相当吻合（该论文在代码中引用了Baxter等人）。由于更新函数是事件数量的期望值，因此对于大的t，它近似等于t/mu，其中mu是事件之间的平均时间；这是知道我们是否处于附近的一种方便方式。

我正在使用Maxima（http://maxima.sourceforge.net）进行工作，它不适用于数值处理，但使得尝试不同方面非常容易。此时，将最终的数值处理转换到另一种语言（如Python）将很简单。

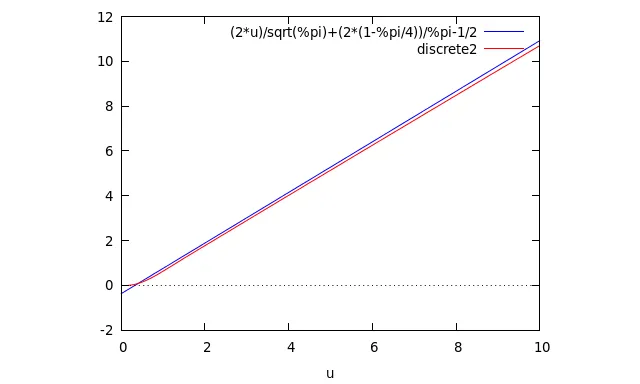
感谢 OP 提出这个问题，以及 S. Pappadeux 进行深入的讨论。下面是我得到的图表，将离散逼近（红色）与大 t 的逼近（蓝色）进行比较。尝试了一些不同步长的例子后，我发现随着步长变小，数值有点增加，因此我认为红线可能有点偏低，而蓝线可能更接近正确。

这是我的Maxima代码：

/* discretize weibull renewal function and formulate system of linear equations
 * copyright 2020 by Robert Dodier
 * I release this work under terms of the GNU General Public License
 *
 * This is a program for Maxima, a computer algebra system.
 * http://maxima.sourceforge.net/
 */

"Definition of the renewal function m(t):" $

renewal_eq: m(t) = F(t) + 'integrate (m(t - s)*f(s), s, 0, t);

"Approximate integral equation with rectangle rule:" $

discretize_renewal (delta_t, k) :=
  if equal(k, 0)
    then m(0) = F(0)
    else m(k*delta_t) =   F(k*delta_t)
                        + m(k*delta_t)*f(0)*(delta_t / 2)
                        + sum (m((k - j)*delta_t)*f(j*delta_t)*delta_t, j, 1, k - 1)
                        + m(0)*f(k*delta_t)*(delta_t / 2);

make_eqs (n, delta_t) :=
  makelist (discretize_renewal (delta_t, k), k, 0, n);

make_vars (n, delta_t) :=
  makelist (m(k*delta_t), k, 0, n);

"Discretized integral equation and variables for n = 4, delta_t = 1/2:" $

make_eqs (4, 1/2);
make_vars (4, 1/2);

make_eqs_vars (n, delta_t) :=
  [make_eqs (n, delta_t), make_vars (n, delta_t)];

load (distrib);
subst_pdf_cdf (shape, scale, e) :=
  subst ([f = lambda ([x], pdf_weibull (x, shape, scale)), F = lambda ([x], cdf_weibull (x, shape, scale))], e);

matrix_from (eqs, vars) :=
 (augcoefmatrix (eqs, vars),
  [submatrix (%%, length(%%) + 1), - col (%%, length(%%) + 1)]);

"Subsitute Weibull pdf and cdf for shape = 2 into discretized equation:" $

apply (matrix_from, make_eqs_vars (4, 1/2));
subst_pdf_cdf (2, 1, %);

"Just the  right-hand side matrix:" $

rhs_matrix_from (eqs, vars) :=
 (map (rhs, eqs),
  augcoefmatrix (%%, vars),
  [submatrix (%%, length(%%) + 1), col (%%, length(%%) + 1)]);

"Generate the right-hand side matrix, instead of extracting it from equations:" $

generate_rhs_matrix (n, delta_t) :=
  [delta_t * genmatrix (lambda ([i, j], if i = 1 and j = 1 then 0
                                        elseif j > i then 0
                                        elseif j = i then f(0)/2
                                        elseif j = 1 then f(delta_t*(i - 1))/2
                                        else f(delta_t*(i - j))), n + 1, n + 1),
   transpose (makelist (F(k*delta_t), k, 0, n))];

"Generate numerical right-hand side matrix, skipping over formulas:" $

generate_rhs_matrix_numerical (shape, scale, n, delta_t) :=
  block ([f, F, numer: true], local (f, F),
         f: lambda ([x], pdf_weibull (x, shape, scale)),
         F: lambda ([x], cdf_weibull (x, shape, scale)),
         [genmatrix (lambda ([i, j], delta_t * if i = 1 and j = 1 then 0
                                               elseif j > i then 0
                                               elseif j = i then f(0)/2
                                               elseif j = 1 then f(delta_t*(i - 1))/2
                                               else f(delta_t*(i - j))), n + 1, n + 1),
          transpose (makelist (F(k*delta_t), k, 0, n))]);

"Solve approximate integral equation (shape = 3, t = 1) via LU decomposition:" $

fpprintprec: 4 $
n: 20 $
t: 1;
[AA, bb]: generate_rhs_matrix_numerical (3, 1, n, t/n);
xx_by_lu: linsolve_by_lu (ident(n + 1) - AA, bb, floatfield);

"Iterative solution of approximate integral equation (shape = 3, t = 1):" $

xx: bb;
for i thru 10 do xx: AA . xx + bb;
xx - (AA.xx + bb);
xx_iterative: xx;

"Should find iterative and LU give same result:" $

xx_diff: xx_iterative - xx_by_lu[1];
sqrt (transpose(xx_diff) . xx_diff);

"Try shape = 2, t = 10:" $

n: 100 $
t: 10 $
[AA, bb]: generate_rhs_matrix_numerical (2, 1, n, t/n);
xx_by_lu: linsolve_by_lu (ident(n + 1) - AA, bb, floatfield);

"Baxter, et al., Eq. 3 (for large values of t) compared to discretization:" $
/* L.A. Baxter, E.M. Scheuer, D.J. McConalogue, W.R. Blischke.
 * "On the Tabulation of the Renewal Function,"
 * Econometrics, vol. 24, no. 2 (May 1982).
 * H(t) is their notation for the renewal function.
 */
H(t) := t/mu + sigma^2/(2*mu^2) - 1/2;

tx_points: makelist ([float (k/n*t), xx_by_lu[1][k, 1]], k, 1, n);

plot2d ([H(u), [discrete, tx_points]], [u, 0, t]), mu = mean_weibull(2, 1), sigma = std_weibull(2, 1);

- Robert Dodier

---

非常感谢。我无法安装Maxima 5.44.0软件。我收到一个错误，显示“C：\ maxima-5.44.0 \ clisp-2.49 \ ANNOUNCE”。 - score324

很难确定问题所在。我的建议是在Maxima邮件列表中发帖。请参阅：https://sourceforge.net/projects/maxima/lists/maxima-discuss - Robert Dodier

Answer 2

我认为这不会起作用。首先，让我们将m(t)中的Γ(2k+1)从分母移到A_k中。因此，A_k的行为大致相当于1/k!。

在m(t)项的分子中有t^2k，因此粗略地说，您正在计算具有以下术语的总和：

100^k/k!

根据斯特林公式，

k！~ k^k，使术语

（100/k）^k 因此，是的，它们将开始减少并收敛到某些值，但是在第100个术语之后。

无论如何，这是代码，您可以尝试改进它，但是在k〜70时会中断。

N <- 20
A <- rep(0, N)

# compute A_k/gamma(2k+1) terms
ps <- 0.0 # previous sum
A[1] = 1.0
for(k in 2:N) {
    ps <- ps + A[k-1]*gamma(2*(k-1) + 1)/factorial(k-1)
    A[k] <- 1.0/factorial(k) - ps/gamma(2*k+1)
}

print(A)

t <- 10.0
t2 <- t*t

r <- 0.0
for(k in 1:N){
    r <- r + (-t2)^k*A[k]
}

print(-r)

更新

好的，我按照你的问题计算了A_k，得到了相同的答案。我想要从m(t)中估计出A_k/Γ(2k+1)的项，我相信它将会被1/k!这一项所主导。为了做到这一点，我又创建了一个数组k!*A_k/Γ(2k+1)，它应该接近于1。

代码

N <- 20
A <- rep(0.0, N)

psum <- function( pA, k ) {
    ps <- 0.0
    if (k >= 2) {
        jmax <- k - 1
        for(j in 1:jmax) {
            ps <- ps + (gamma(2*j+1)/factorial(j))*pA[k-j]
        }
    }
    ps
}

# compute A_k/gamma(2k+1) terms
A[1] = gamma(3)
for(k in 2:N) {
    A[k] <- gamma(2*k+1)/factorial(k) - psum(A, k)
}

print(A)

B <- rep(0.0, N)
for(k in 1:N) {
    B[k] <- (A[k]/gamma(2*k+1))*factorial(k)
}

print(B)

显示了

1. 我得到了与您相同的A_k值。
2. B_k确实非常接近于1

这意味着项A_k/Γ(2k+1)可以被替换为1/k!，以便快速估计我们可能会得到的内容（进行替换）

m(t) ~= - Sum(k=1, k=Infinity) (-1)^k (t²)^k / k! = 1 - Sum(k=0, k=Infinity) (-t²)^k / k!

这实际上是一个众所周知的总和，等于带有负参数的exp()（好吧，您必须添加k=0的项）

m(t) ~= 1 - exp(-t²)

结论

1. 近似值为正。可能会一直保持积极，因为A_k/Γ(2k+1)与1/k!略有不同。

2. 我们正在谈论1 - exp(-100)，它为1-3.72*10^-44！而我们试图通过求和和减去高达10¹⁰⁰甚至更高的值来精确计算它。即使使用MPFR，我认为这也是不可能的。

需要另一种方法

- Severin Pappadeux

---

“m(t)”始终为正数。更新函数不能为负数。 - score324

有没有一种简单的方法来指定算术应该是任意精度的？我猜可能至少有两种类型是相关的——一种是任意精度整数，另一种是任意精度浮点数。我不知道在 R 中可能有什么。 - Robert Dodier

是的，我认为下一步要尝试的是以某种方式重新排列求和。此外，在这种情况下，精确或任意精度算术也不会有害。 - Robert Dodier

@RobertDodier 你可能是对的，它可能会有很大的偏差。但我认为仍然不可能通过运行OP问题中的公式来计算。在这一点上，如果t = 10且m = 2相关，则我认为OP需要寻找t^m的渐近逼近。是的，我同意，比如对于非常大的参数，(1/t)^mk的级数将是很好的选择。 - Severin Pappadeux

@SeverinPappadeux 另一种看起来可行的方法是观察续存函数满足的积分方程，m(t) = F(t) + integral(m(t - s) f(s), s from 0 to t)，其中f和F分别是概率密度和累积密度。我认为可以通过将其离散化为线性方程组来传统地进行近似。 - Robert Dodier