拟合由4个（或更多）XYZ点组成的平面

Question

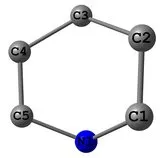
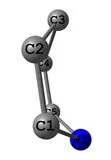
我有四个点，它们非常接近于在同一平面上 - 这是1,4-二氢吡啶环。

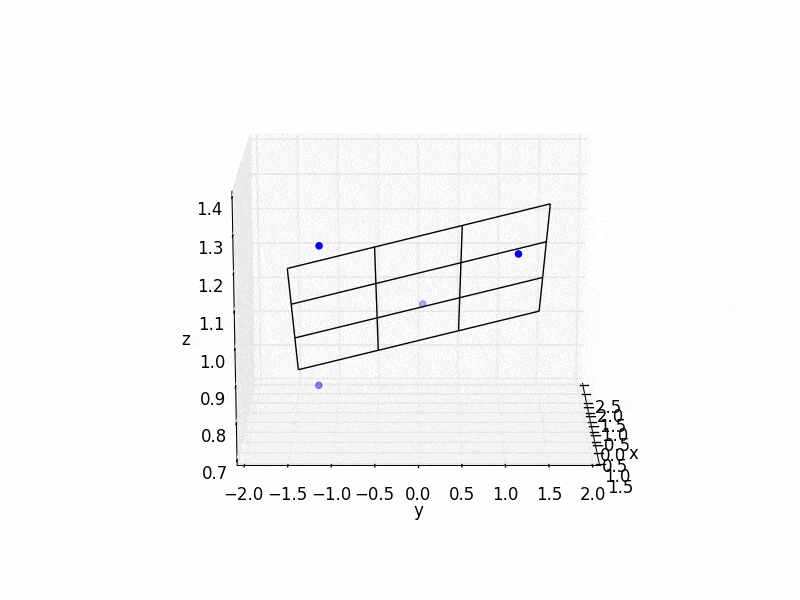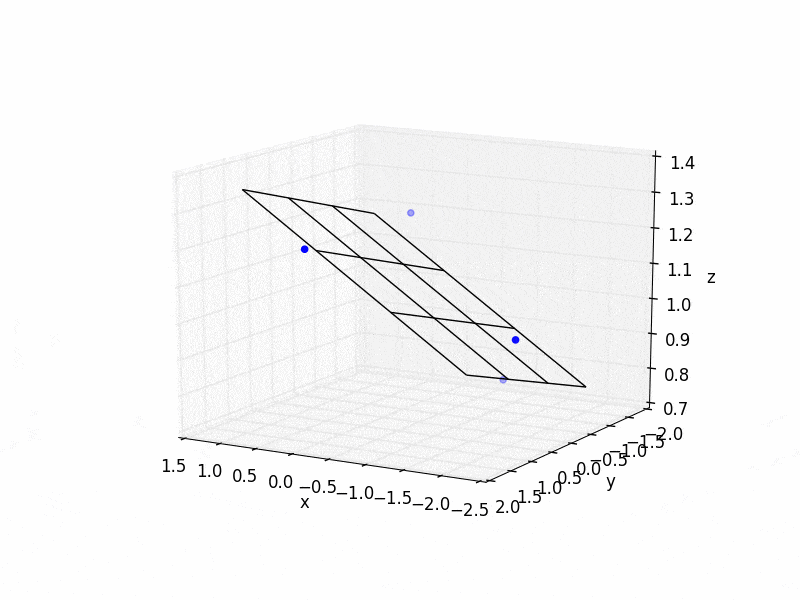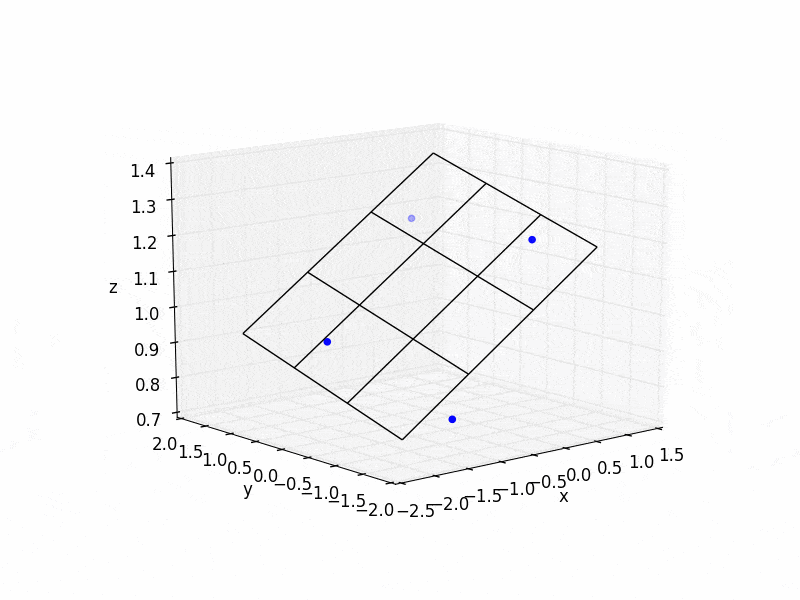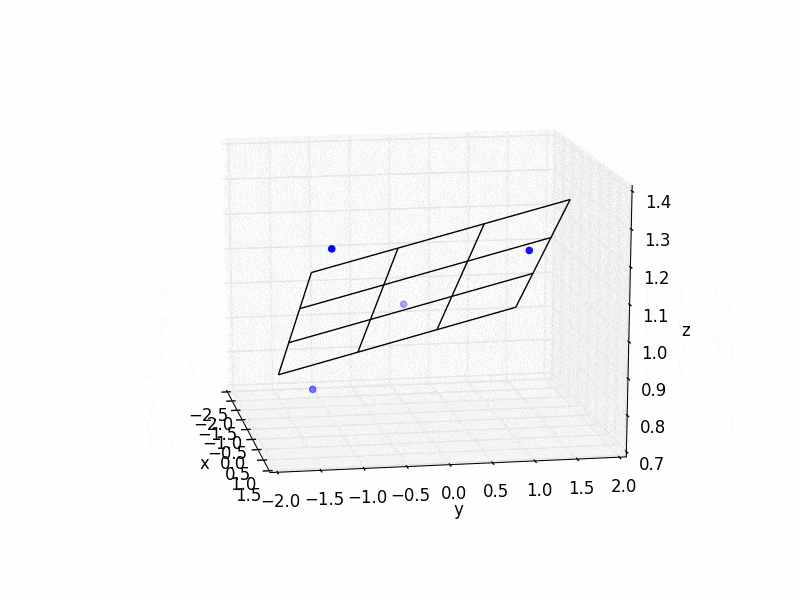
我需要计算从C3和N1到平面的距离，该平面由C1-C2-C4-C5组成。计算距离很简单，但是拟合平面对我来说非常困难。

1,4-DHP环：

1,4-DHP环的另一个视角：

from array import *
from numpy import *
from scipy import *

# coordinates (XYZ) of C1, C2, C4 and C5
x = [0.274791784, -1.001679346, -1.851320839, 0.365840754]
y = [-1.155674199, -1.215133985, 0.053119249, 1.162878076]
z = [1.216239624, 0.764265677, 0.956099579, 1.198231236]

# plane equation Ax + By + Cz = D
# non-fitted plane
abcd = [0.506645455682, -0.185724560275, -1.43998120646, 1.37626378129]

# creating distance variable
distance =  zeros(4, float)

# calculating distance from point to plane
for i in range(4):
    distance[i] = (x[i]*abcd[0]+y[i]*abcd[1]+z[i]*abcd[2]+abcd[3])/sqrt(abcd[0]**2 + abcd[1]**2 + abcd[2]**2)
    
print distance

# calculating squares
squares = distance**2

print squares

如何使平方和最小化？我尝试了最小二乘法，但对我来说太难了。

- XuMuK

---

尝试在math.stackexchange上询问吗？您目前似乎不需要编码帮助 :) - Shark

我不确定在这种情况下提到“1,4-二氢吡啶环”是否有帮助。你是否已经谷歌搜索了“Python平面拟合”？第五个结果看起来很有前途... - user1071136

我在这里写了一个类似的答案（https://dev59.com/MGDVa4cB1Zd3GeqPcVMo#9243785），可能会有用（只需忽略关于权重的最后一部分）。 - YXD

@MrE链接的信息对于理解我的解决方案在幕后所做的事情至关重要，否则你只是在处理一个神奇的黑匣子。 - Hooked

是的！最困难的是理解距离是如何计算的。 - XuMuK

你假设你的Google搜索结果与读者的搜索结果相同，并且这种搜索结果随着时间的推移保持不变，但这两点都是不正确的。提供一个链接比含糊地建议“你应该谷歌搜索‘这个’并点击第n个结果”更有帮助。为了证明我的观点，目前在DuckDuckGo上进行这样的搜索的第一个结果就是StackOverflow上的这个问题。 - ArtOfWarfare

Answer 1

听起来大概是正确的，但你应该用SVD代替非线性优化。以下代码创建了惯性张量M，然后对其进行SVD以获取平面法线。这应该是最小二乘拟合的一个很好的近似，并且速度更快、更可预测。它返回点云中心和法线。

def planeFit(points):
    """
    p, n = planeFit(points)

    Given an array, points, of shape (d,...)
    representing points in d-dimensional space,
    fit an d-dimensional plane to the points.
    Return a point, p, on the plane (the point-cloud centroid),
    and the normal, n.
    """
    import numpy as np
    from numpy.linalg import svd
    points = np.reshape(points, (np.shape(points)[0], -1)) # Collapse trialing dimensions
    assert points.shape[0] <= points.shape[1], "There are only {} points in {} dimensions.".format(points.shape[1], points.shape[0])
    ctr = points.mean(axis=1)
    x = points - ctr[:,np.newaxis]
    M = np.dot(x, x.T) # Could also use np.cov(x) here.
    return ctr, svd(M)[0][:,-1]

例如：在(10,100)处构建一个二维云，该云在x方向上很薄，在y方向上比原来大100倍。

>>> pts = np.diag((.1, 10)).dot(randn(2,1000)) + np.reshape((10, 100),(2,-1))

拟合平面非常接近于点（10，100），法线几乎沿着x轴方向。

>>> planeFit(pts)

    (array([ 10.00382471,  99.48404676]),
     array([  9.99999881e-01,   4.88824145e-04]))

- Ben

---

但是Hooked的答案非常精确; 测量单位是埃（不需要百分之一的精度），而且我的数据点并不多 - 速度还可以。但是这看起来是一个非常有趣的解决方案。 - XuMuK

使用scipy.optimize.leastsq是很好的，但（假设我没有添加错误），这是进行总最小二乘法的正确方式。http://en.wikipedia.org/wiki/Total_least_squares - Ben

为什么这会变得不太准确呢？实际上，这比非线性优化更加精确。 - vidstige

我现在对这个有点生疏了。我当时的想法是，总最小二乘法是平方误差的和，而奇异值分解（SVD）的解将给你（我认为）rsin(theta)的平方和。当然，对于较小的theta，rsin(theta)非常接近欧几里得误差，但对于较大的误差来说则不太一样。 - Ben

谢谢你的代码！顺便提一下，如果你需要回到一个平面方程，其中点r（x，y...）在平面上找到，法向量n，那么如果点满足以下条件：n⋅(r−b) = 0，那么它就在平面上。 - undefined

Answer 2

最小二乘法能够轻松拟合平面。平面的方程式为：ax + by + c = z。所以，使用所有数据设置以下矩阵：

    x_0   y_0   1  
A = x_1   y_1   1  
          ... 
    x_n   y_n   1  

并且

    a  
x = b  
    c

并且

    z_0   
B = z_1   
    ...   
    z_n

换句话说：Ax = B。现在解出x，这些是您的系数。但是由于您有超过3个点，系统是超定的，因此您需要使用左伪逆。所以答案是：

a 
b = (A^T A)^-1 A^T B
c

以下是一个简单的Python代码示例：

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

N_POINTS = 10
TARGET_X_SLOPE = 2
TARGET_y_SLOPE = 3
TARGET_OFFSET  = 5
EXTENTS = 5
NOISE = 5

# create random data
xs = [np.random.uniform(2*EXTENTS)-EXTENTS for i in range(N_POINTS)]
ys = [np.random.uniform(2*EXTENTS)-EXTENTS for i in range(N_POINTS)]
zs = []
for i in range(N_POINTS):
    zs.append(xs[i]*TARGET_X_SLOPE + \
              ys[i]*TARGET_y_SLOPE + \
              TARGET_OFFSET + np.random.normal(scale=NOISE))

# plot raw data
plt.figure()
ax = plt.subplot(111, projection='3d')
ax.scatter(xs, ys, zs, color='b')

# do fit
tmp_A = []
tmp_b = []
for i in range(len(xs)):
    tmp_A.append([xs[i], ys[i], 1])
    tmp_b.append(zs[i])
b = np.matrix(tmp_b).T
A = np.matrix(tmp_A)
fit = (A.T * A).I * A.T * b
errors = b - A * fit
residual = np.linalg.norm(errors)

print("solution: %f x + %f y + %f = z" % (fit[0], fit[1], fit[2]))
print("errors:")
print(errors)
print("residual: {}".format(residual))

# plot plane
xlim = ax.get_xlim()
ylim = ax.get_ylim()
X,Y = np.meshgrid(np.arange(xlim[0], xlim[1]),
                  np.arange(ylim[0], ylim[1]))
Z = np.zeros(X.shape)
for r in range(X.shape[0]):
    for c in range(X.shape[1]):
        Z[r,c] = fit[0] * X[r,c] + fit[1] * Y[r,c] + fit[2]
ax.plot_wireframe(X,Y,Z, color='k')

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()

您的问题的解决方案如下：

0.143509 x + 0.057196 y + 1.129595 = z

- Ben

---

谢谢你的回答。当我提出这个问题时，我对def函数的工作原理一无所知。而且我找不到任何已经可用于我的任务的东西。 - XuMuK

该方法对奇异矩阵不够健壮。将尝试其他方法。 - Nathan majicvr.com

@Frank 这个解决方案不是迭代的，也不是机器学习。它只是最小二乘法，这只是一种直接的数学方法，可以最小化模型误差。不，这不能处理奇异矩阵，我也不确定怎么做才行。我认为这意味着问题的表述存在根本性错误。 - Ben

这在Python3 / 新的numpy中不起作用。如果可以请帮我修改，因为我自己无法做到。 - Gulzar

@Gulzar，只需要更新print()函数以适应Python3即可，现在应该可以工作了。 - Ben

Answer 3

你正在拟合一个平面的事实在此只是略微相关。你试图做的是从一个猜测开始最小化一个特定的函数。为此，请使用scipy.optimize。请注意，这不是全局最优解，只是局部最优解。不同的初始条件可能会收敛到不同的结果，如果你从接近所寻找的局部极小值的位置开始，则效果很好。

我已经利用numpy的广播功能对你的代码进行了清理:

import numpy as np

# coordinates (XYZ) of C1, C2, C4 and C5
XYZ = np.array([
        [0.274791784, -1.001679346, -1.851320839, 0.365840754],
        [-1.155674199, -1.215133985, 0.053119249, 1.162878076],
        [1.216239624, 0.764265677, 0.956099579, 1.198231236]])

# Inital guess of the plane
p0 = [0.506645455682, -0.185724560275, -1.43998120646, 1.37626378129]

def f_min(X,p):
    plane_xyz = p[0:3]
    distance = (plane_xyz*X.T).sum(axis=1) + p[3]
    return distance / np.linalg.norm(plane_xyz)

def residuals(params, signal, X):
    return f_min(X, params)

from scipy.optimize import leastsq
sol = leastsq(residuals, p0, args=(None, XYZ))[0]

print("Solution: ", sol)
print("Old Error: ", (f_min(XYZ, p0)**2).sum())
print("New Error: ", (f_min(XYZ, sol)**2).sum())

这将给出：

Solution:  [  14.74286241    5.84070802 -101.4155017   114.6745077 ]
Old Error:  0.441513295404
New Error:  0.0453564286112

- Hooked

---

这段代码即使有超过4个点也能正常工作...是吧？ 只需将坐标添加到第一个数组中即可。 - user1941583

@Hooked你说“局部最优”，但是有没有一种方法可以保证全局最优解而不考虑初始条件？我自己对线性代数不够了解。 - Nathan majicvr.com

@frank 一般来说，对于任意成本函数，无法保证你处于全局最小值而非局部最小值。然而，在一个重要的（线性）问题子集中，我们可以保证并在多项式时间内找到解决方案。这实际上是线性代数的主要优势之一。许多非线性问题可以近似为线性问题，因此您可以精确地解决近似问题。 - Hooked

难道不应该最小化的是绝对距离吗？ - Niranjan Kotha

@NiranjanKotha 这取决于具体情况！L1和L2范数（绝对值与均方差）总是给出相同的排名，但它们是衡量你离目标有多远的不同度量。对于迭代求解器来说，这意味着它们具有相同的最小值（因此具有相同的“正确”答案），但梯度不同。不同的梯度允许某些求解器更快地到达解决方案。在许多情况下，但并非所有情况下，L2范数收敛更快。 - Hooked

@frank Scipy有一种寻找全局最小值的方法。 - user10121139

Answer 4

此函数返回3D平面系数以及拟合的均方根误差(RMSE)。

该平面使用齐次坐标表示，意味着它与点的齐次坐标进行点积所得到的结果是两者之间的距离。

def fit_plane(points):
    assert points.shape[1] == 3
    centroid = points.mean(axis=0)
    x = points - centroid[None, :]
    U, S, Vt = np.linalg.svd(x.T @ x)
    normal = U[:, -1]
    origin_distance = normal @ centroid
    rmse = np.sqrt(S[-1] / len(points))
    return np.hstack([normal, -origin_distance]), rmse

小注：SVD也可以直接应用于点而不是外积矩阵，但我发现使用NumPy的SVD实现时速度较慢。

U, S, Vt = np.linalg.svd(x.T, full_matrices=False)
rmse = S[-1] / np.sqrt(len(points))

- Martin Valgur

Answer 5

在处理异常值时（当您有大型数据集时），除了SVD之外，另一种快速解决方案是RANSAC：

def fit_plane(voxels, iterations=50, inlier_thresh=10):  # voxels : x,y,z
    inliers, planes = [], []
    xy1 = np.concatenate([voxels[:, :-1], np.ones((voxels.shape[0], 1))], axis=1)
    z = voxels[:, -1].reshape(-1, 1)
    for _ in range(iterations):
        random_pts = voxels[np.random.choice(voxels.shape[0], voxels.shape[1] * 10, replace=False), :]
        plane_transformation, residual = fit_pts_to_plane(random_pts)
        inliers.append(((z - np.matmul(xy1, plane_transformation)) <= inlier_thresh).sum())
        planes.append(plane_transformation)
    return planes[np.array(inliers).argmax()]


def fit_pts_to_plane(voxels):  # x y z  (m x 3)
    # https://math.stackexchange.com/questions/99299/best-fitting-plane-given-a-set-of-points
    xy1 = np.concatenate([voxels[:, :-1], np.ones((voxels.shape[0], 1))], axis=1)
    z = voxels[:, -1].reshape(-1, 1)
    fit = np.matmul(np.matmul(np.linalg.inv(np.matmul(xy1.T, xy1)), xy1.T), z)
    errors = z - np.matmul(xy1, fit)
    residual = np.linalg.norm(errors)
    return fit, residual

- Dan Erez

---

体素应该给出非常接近的结果，但看起来需要更多的编码！ - XuMuK

我不确定你的意思，但是体素在原问题中相当于XYZ - 你不需要以某种方式预处理它们。 - Dan Erez

Answer 6

这里有一种方法。如果你的点是P[1]..P[n]，那么计算它们的平均值M，并从每个点中减去它，得到点p[1]..p[n]。然后计算C = Sum{ p[i]*p[i]'}（点的“协方差”矩阵）。接下来对C进行对角化，即找到正交矩阵U和对角矩阵E，使得C = U*E*U'。如果你的点确实在一个平面上，那么其中一个特征值（即E的对角线条目）将非常小（在完美的算术中为0）。无论如何，如果其中第j个是最小的，则让U的第j列为（A，B，C），并计算D = -M'*N。这些参数定义了“最佳”平面，即使得从P[]到平面的距离的平方和最小的平面。

- dmuir

---

这是非常快的方法，但我需要确切的最小二乘法。 - XuMuK