logo标签列表

为什么在将乘法转换为循环内加法后，这段代码的执行速度变慢了？

assemblyoptimizationx86-64cpu-architecturesimd
320

我正在阅读Agner Fog的优化手册，然后看到了这个例子:

double data[LEN];

void compute()
{
    const double A = 1.1, B = 2.2, C = 3.3;

    int i;
    for(i=0; i<LEN; i++) {
        data[i] = A*i*i + B*i + C;
    }
}

Agner指出有一种优化这段代码的方法——意识到循环可以避免使用昂贵的乘法，而是使用每次迭代应用的“增量”。

我先用一张纸确认这个理论...

Theory

当然，他是对的——在每个循环迭代中，我们可以通过添加“delta”来基于旧结果计算新结果。这个delta从值“A+B”开始，然后在每一步上增加“2*A”。

因此，我们更新代码如下：

void compute()
{
    const double A = 1.1, B = 2.2, C = 3.3;
    const double A2 = A+A;
    double Z = A+B;
    double Y = C;

    int i;
    for(i=0; i<LEN; i++) {
        data[i] = Y;
        Y += Z;
        Z += A2;
    }
}

从操作复杂性来看，这两个函数版本的差异确实很明显。相对于加法，乘法在我们的CPU中被认为是明显较慢的。我们已经用2个加法代替了3个乘法和2个加法……

因此，我添加一个循环来执行compute很多次，然后保留执行所需的最短时间：

unsigned long long ts2ns(const struct timespec *ts)
{
    return ts->tv_sec * 1e9 + ts->tv_nsec;
}

int main(int argc, char *argv[])
{
    unsigned long long mini = 1e9;
    for (int i=0; i<1000; i++) {
        struct timespec t1, t2;
        clock_gettime(CLOCK_MONOTONIC_RAW, &t1);
        compute();
        clock_gettime(CLOCK_MONOTONIC_RAW, &t2);
        unsigned long long diff = ts2ns(&t2) - ts2ns(&t1);
        if (mini > diff) mini = diff;
    }
    printf("[-] Took: %lld ns.\n", mini);
}

我编译了两个版本，运行它们... 然后看到了这个：

gcc -O3 -o 1 ./code1.c

gcc -O3 -o 2 ./code2.c

./1

[-] Took: 405858 ns.

./2

[-] Took: 791652 ns.

哦，这很意外。由于我们报告的是最短执行时间，因此我们排除了操作系统的各个部分引起的“噪音”。我们还特别注意在一台什么都不做的机器上运行。结果或多或少是可重复的 - 重新运行这两个二进制文件表明这是一个一致的结果：

for i in {1..10} ; do ./1 ; done

[-] Took: 406886 ns.
[-] Took: 413798 ns.
[-] Took: 405856 ns.
[-] Took: 405848 ns.
[-] Took: 406839 ns.
[-] Took: 405841 ns.
[-] Took: 405853 ns.
[-] Took: 405844 ns.
[-] Took: 405837 ns.
[-] Took: 406854 ns.

for i in {1..10} ; do ./2 ; done

[-] Took: 791797 ns.
[-] Took: 791643 ns.
[-] Took: 791640 ns.
[-] Took: 791636 ns.
[-] Took: 791631 ns.
[-] Took: 791642 ns.
[-] Took: 791642 ns.
[-] Took: 791640 ns.
[-] Took: 791647 ns.
[-] Took: 791639 ns.

接下来要做的就是看编译器为这两个版本生成了什么样的代码。

objdump -d -S 显示 compute 的第一个版本——“笨拙但快速”的代码有一个如下所示的循环：

objdump naive

第二个优化版本怎么样 - 只执行了两次加法操作？

objdump optimized

现在我不知道你，但就我而言，我感到有些困惑。第二个版本的指令数量大约少了4倍，其中两个主要指令只是基于SSE的加法(addsd)。第一个版本不仅有4倍的指令......也充满了乘法(mulpd)，这是预期的。

我承认我没有预料到这个结果。这不是因为我是Agner的粉丝（虽然我是），但这与此无关。

你有什么想法吗？我有没有犯任何错误可以解释速度差异？请注意，我在Xeon W5580和Xeon E5-1620上进行了测试，在两者中，第一个（愚蠢的）版本比第二个版本快得多。

为了方便重现结果，这里有两个代码版本的gist：Dumb yet somehow faster和optimized, yet somehow slower。

P.S. 请不要评论浮点精度问题；这不是这个问题的重点。

73
原始代码容易进行向量化，新版本存在循环依赖，无法进行向量化。因此，在第二个版本中，除了缺乏向量化之外，您还失去了OOO处理器一次执行多个迭代的能力。 - fuz
7
这些时间数值是哪个CPU的？你提到了两个旧的Xeon CPU，一个是W5580（Nehalem-EP），另一个是E5-1620（Sandybridge-EP）。这两个CPU都有每个时钟1/clock的浮点加法和乘法吞吐量，在不同的端口上以便并行运行。只有Skylake及以后的CPU才具有每个时钟2/clock的加法吞吐量。但它们所有的FPU都具有流水线结构，延迟相对较大，而吞吐量相对较小，因此，正如phuclv和fuz指出的那样，循环依赖是一个巨大的问题。 - Peter Cordes
4
为了将2元素相加的版本向量化，您需要手动展开，并以4*A2的增量进行。可能使用-ffast-math可以让clang为您完成这项工作（甚至可能是GCC，但GCC倾向于不使用多个累加器展开）。对于Haswell或更高版本的处理器，使用Horner方法处理这样一个简短的多项式非常适合，并且易于应用程序执行顺序隐藏，尽管它仍需要i的FP版本。 - Peter Cordes
11
我想提一下，在整数运算中，乘法比加法更耗费时间；但是对于浮点数来说通常情况相反（加法更耗费时间）。原因是对于浮点数乘法，显式位和指数可以独立并行确定（例如显式位 = sig1 * sig2; 指数 = exp1 + exp2），而对于浮点数加法，则需要依次完成（确定结果的指数，然后“移位”两个值以匹配结果指数，然后确定结果的显式位）。 - Brendan
5
@Brendan: 尽管如此，现代x86硬件FPUs的乘法延迟始终至少与加法相同。尾数相乘仍然是一个24或53位整数乘法。但是，如果您采用微码辅助来处理次正常输入或输出，那么可以使快速路径变得非常短。请查看https://uops.info/，以获取“mulpd”与“addpd”（以及“vfma…”）之间的比较。 Alder Lake将“addpd”的延迟改进为3个周期，从Skylake以来addpd / subpd / mulpd / vfma…pd的延迟为4个周期。 AMD在某些CPU上有更低的加法延迟，但Zen2的addpd和mulpd的延迟为3个时钟周期，而fma为5个时钟周期，就像Broadwell一样。 - Peter Cordes
显示剩余7条评论
7个回答
314
理解性能差异的关键在于向量化。是的，基于加法的解决方案在其内部循环中只有两条指令，但重要的区别不在于循环中有多少指令，而在于每个指令执行了多少工作。
在第一个版本中，输出仅取决于输入：每个data[i]只是i本身的函数，这意味着可以以任何顺序计算每个data[i]：编译器可以向前、向后、侧向等方式进行计算，你仍然会得到相同的结果——除非你正在观察来自另一个线程的内存，否则你永远不会注意到数据被压缩的方式。
在第二个版本中，输出不依赖于i——它依赖于上次循环中的A和Z。
如果我们将这些循环的主体表示为小的数学函数，它们的整体形式将非常不同：
  • f(i) -> di
  • f(Y, Z) -> (di, Y', Z')
在后一种形式中，实际上并没有依赖于i——你可以通过知道上一次调用函数的Y和Z来计算函数的值，这意味着函数形成了一个链——你不能做下一个直到完成前一个。
为什么这很重要？因为CPU具有向量并行指令，每个指令可以同时执行两个、四个甚至八个算术操作！（AVX CPU可以并行执行更多操作。）那就是四个乘法、四个加法、四个减法、四个比较——四个任何东西！所以，如果你要计算的输出仅依赖于输入，那么你可以安全地一次执行两个、四个或甚至八个——无论它们是向前还是向后，因为结果都是相同的。但如果输出依赖于先前的计算，那么你只能按顺序进行——一个接一个地进行。
这就是为什么“更长”的代码在性能上胜出的原因。即使它有很多设置，并且实际上正在执行更多的工作，但大部分工作都是并行完成的：它不仅在每次循环迭代中计算data[i]，还同时计算data[i+1]、data[i+2]和data[i+3]，然后跳到下一组四个。

为了更好地解释我的意思，编译器首先将原始代码转换成以下内容：

int i;
for (i = 0; i < LEN; i += 4) {
    data[i+0] = A*(i+0)*(i+0) + B*(i+0) + C;
    data[i+1] = A*(i+1)*(i+1) + B*(i+1) + C;
    data[i+2] = A*(i+2)*(i+2) + B*(i+2) + C;
    data[i+3] = A*(i+3)*(i+3) + B*(i+3) + C;
}

如果你眯起眼睛看的话，你可以相信它会做与原始代码相同的事情。这是由于所有这些相同的操作符垂直线造成的：所有这些*和+操作都是相同的操作，只是在不同的数据上执行 - CPU具有特殊的内置指令，可以在每个时钟周期中对不同的数据执行多个*或多个+操作。
注意快速解决方案中指令中的字母p - addpd和mulpd，以及较慢解决方案中指令中的字母s - addsd。那是“添加打包双精度”和“乘以打包双精度”，而“添加单精度”则相对较慢。
此外，似乎编译器部分展开了循环-循环不仅在每次迭代中执行两个值，而实际上是四个，并交错操作以避免依赖关系和停顿，所有这些都减少了汇编代码必须测试i < 1000 的次数。
然而，所有这些仅在循环之间存在没有依赖性的情况下才起作用：如果决定每个data [i]发生什么的唯一因素是i本身。如果存在依赖关系，如果上一次迭代的数据影响下一次迭代，则编译器可能受到它们的限制，无法改变代码 - 而不是编译器能够使用花哨的并行指令或巧妙的优化（CSE，strength reduction，loop unrolling，重新排序等），你得到的是完全与输入相同的代码-首先添加Y，然后添加Z，然后重复。
但是，在代码的第一个版本中，编译器正确地识别出数据中没有依赖关系，并计算出可以并行处理的工作，因此它就这样做了，这就是使所有差异的原因。
44
不仅仅是向量化，还有数据依赖关系。由于迭代之间的延迟瓶颈，来自“优化”版本的标量代码不能以最高速度运行。这也是阻止它向量化的原因，但如果没有循环传递依赖性，就可以实现向量化和跨迭代的指令级并行处理。 （整数 i++ 是循环传递依赖关系，但编译器可以操作它，因为整数数学是可结合的，不像没有 -ffast-math 的浮点数）。 - Peter Cordes
24
@PeterCordes，我真的想在这个答案中专注于“并行计算与串行计算”的高层概念，因为这似乎是问题的根源 - 如果你甚至不知道并行指令的存在，那么你会像提问者一样困惑，不知道如何将“更多”转变为“更少”。依赖关系和瓶颈 - 编译器确定可用的优化选项的方式 - 将是很好的后续问题。 - Sean Werkema
13
指令级并行与SIMD并行同样重要。也许更重要，因为在Nehalem和Sandy Bridge上，每个向量只有2个double，而SIMD FP addsd/addpd的延迟为3个时钟周期，吞吐量为1个时钟周期。尽管在循环中有两个独立的加法链，但这可能意味着每1.5个时钟周期就会有一个标量FP加法，因此可能SIMD更重要。 - Peter Cordes
12
在循环迭代中存在串行依赖性实际上是实现并行与串行代码（以及执行该代码）的最终关键，我认为这将是一个很好的开头段落。编译器和CPU可以以多种方式利用它，编译器自动矢量化，CPU则利用独立循环迭代的ILP。即使您只想谈论SIMD矢量化，在循环中发现可用的数据并行性是关键的第一步观察。（我已经为这个答案点了赞；总体而言不错，但我希望它从并行性vs.依赖性开始）。 - Peter Cordes
8
在您的更新中，提到了“strength-reduction optimization”（强度降低优化）。问题中提出的优化 是 强度降低的一个高级案例，将独立乘法替换为循环内的累加链。因此，如果编译器使用“-ffast-math”实现该优化，希望以不影响展开向量化的方式进行。 - Peter Cordes
显示剩余6条评论
65
这里的主要区别在于循环依赖关系。第二种情况下的循环是“依赖性”的——循环中的操作依赖于上一个迭代。这意味着每次迭代都无法开始，直到上一个迭代完成。而在第一种情况下，循环体是完全“独立”的——循环体中的所有内容都是自包含的，仅取决于迭代计数器和常量值。这意味着循环可以并行计算——多个迭代可以同时进行。这样就可以轻松地展开循环并将其向量化，重叠许多指令。
如果您查看性能计数器（例如，使用perf stat ./1命令），您会发现第一个循环不仅运行得更快，而且每个周期也执行了更多的指令（IPC）。相比之下，第二个循环具有更多的依赖周期——CPU 在等待指令完成之前会闲置一段时间，然后才能发出更多指令。

第一种方法可能会出现内存带宽瓶颈，特别是如果你让编译器在 Sandy Bridge 上使用 AVX 自动向量化 (gcc -O3 -march=native)，并且它成功地使用了 256 位向量。此时，IPC 将会下降，特别是对于一个输出数组太大以至于不适合 L3 缓存 的情况。

注意：展开和向量化并不需要独立的循环——即使有一些循环依赖也可以这样做。然而，这种情况更难实现，而且回报较少。因此，如果你想从向量化中获得最大的加速效果，尽可能消除循环依赖将会有所帮助。

1
谢谢 - 这很有道理。同时运行4个，我猜分支比较也会少运行4次。如果您有关于如何读取您所说的性能计数器（在Linux下）的建议，将不胜感激。 - ttsiodras
1
oprofile是在Linux上执行此操作的常规方式。 - Chris Dodd
1
@ttsiodras：现在大多数人使用类似于perf stat --all-user ./1的东西来累积整个程序的计数。这很好，因为它在循环内花费了大部分时间。您可能希望将计时移动到循环外部或删除它以进行此类分析，也许通过将实际工作放在一个__attribute__((noinline,noipa))函数中隐藏重复循环，以阻止程序间分析和内联。 - Peter Cordes
8
为了获得最大的手动向量化效益，我认为您可能会使用版本2，但是使用多个向量以锁定方式前进，其中每个不同的Z和Y向量都有四个向量，例如Z0 += 8 * A2（如果每个Z向量保存4个双精度浮点数而不是2个，则为16*A2）。 您需要进行一些数学计算来考虑在8或16个“i”值中跨越一个元素的步幅，可能需要在其中某个位置进行乘法。 您几乎肯定可以比每次迭代重新执行int-> FP转换更好； 这是一种昂贵的方法来获得独立迭代。 - Peter Cordes
42
这种 有限差分法 的强化减少优化方法，相比于每次单独重新评估多项式，可以 提高速度。但是只有当你将其推广到更大的步长时，才能在循环中保持足够的并行性。 我的版本针对适合L1d缓存的小数组，在Skylake上每个时钟周期存储一个向量（四个双精度数），否则它就是一个带宽测试。在早期的Intel处理器上，包括使用AVX的Sandy Bridge（如果输出对齐），也应该达到SIMD FP-add吞吐量的最大值（每两个时钟周期1x 256位加法和1x 256位存储）。

依赖于上一次迭代的值会导致性能下降

这种强度降低优化（只是简单地加法，而不是重新开始一个新的i并进行乘法运算）在循环迭代中引入了一个串行依赖关系，涉及到浮点数运算而不是整数增量。

原始版本具有每个输出元素的数据并行性：每个元素仅依赖于常量和自己的i值。编译器可以使用SIMD（SSE2或AVX，如果您使用-O3 -march=native）进行自动向量化，而CPU可以通过乱序执行将工作跨越循环迭代重叠。尽管需要额外的工作量，但CPU能够以足够的暴力应用，并获得编译器的帮助。

但是，计算poly(i+1)的版本却具有非常有限的并行性；没有SIMD向量化，例如，在Intel Skylake到Tiger Lake上，四个周期是FP加法的延迟时间，其中您的CPU每四个周期只能运行两个标量加法（https://uops.info/）。

huseyin tugrul buyukisik的答案展示了如何在更现代的CPU上接近最大化原始版本的吞吐量，使用两个FMA操作来评估多项式(Horner's scheme)，加上整数到浮点转换或浮点增量。(后者创建了一个FP依赖链，您需要展开以隐藏。)
因此，在最好的情况下，每个SIMD输出向量有三个浮点数学运算。(加上存储)当前英特尔CPU只有两个浮点执行单元，可以运行包括int-to-double在内的FP数学运算。(对于512位向量，当前CPU关闭端口1上的向量ALU，因此总共只有两个SIMD ALU端口，因此非FP数学运算(如SIMD-integer increment)也将竞争SIMD吞吐量。除了只有一个512位FMA单元的CPU，那么端口5是空闲的，可用于其他工作。)
自Zen 2以来，AMD在两个端口上拥有两个FMA/mul单元和两个不同端口上的两个FP add/sub单元，因此如果使用FMA进行加法，您理论上每个时钟周期最多可以进行四个SIMD加法。
Haswell/Broadwell每个时钟周期有2个FMA，但只有1个FP add/sub (具有较低的延迟)。这对于天真的代码来说很好，但对于已经优化为具有大量并行性的代码来说不是很好。这可能是英特尔在Skylake中进行更改的原因。(Alder Lake重新引入了低延迟FP add/sub，但吞吐量与乘法相同，每个时钟周期2个。有趣的是，非交换延迟:目标只需要2个周期，另一个操作数需要3个周期，因此它非常适用于较长的依赖链。)
您的Sandy Bridge(E5-1620)和Nehalem(W5580) CPU每个时钟周期有1个FP add/sub，1个FP mul，在不同的端口上。这就是Haswell正在构建的内容。这也是为什么添加额外的乘法不是一个大问题：它们可以与现有的加法并行运行。(Sandy Bridge的宽度为256位，但您编译时未启用AVX:使用-march=native。)

寻找并行性：任意步长下的强度降低

您的compute2根据前一个值计算出下一个Y和下一个Z。也就是说，对于data[i+1]，步长为1，您需要的值。因此，每次迭代都依赖于前一个迭代。

如果将其推广到其他步长，则可以提前4、6、8或更多个独立的Y和Z值，使它们彼此锁步跳跃，所有这些值都相互独立。 这恢复了足够的并行性，以便编译器和/或CPU利用它们。

poly(i)   = A i^2           + B i       + C

poly(i+s) = A (i+s)^2       + B (i+s)   + C
          = A*i^2 + A*2*s*i + A*s^2 +  B*i + B*s + C
          = poly(i) + A*2*s*i + A*s^2 + B*s + C

所以这有点混乱，不太清楚如何将其分解为Y和Z部分。（而且此答案的早期版本是错误的。）可能更容易从FP值序列的步幅的一阶和二阶差异开始逆推（有限差分法）。这将直接找到我们需要添加的内容以向前移动；Z []初始化程序和步骤。这基本上就像取一阶和二阶导数，然后优化循环有效地进行积分来恢复原始函数。以下输出由下面基准测试中正确性检查部分生成。
# method of differences for stride=1, A=1, B=0, C=0
poly(i) 1st    2nd  difference from this poly(i) to poly(i+1)
0       1
1       3       2        # 4-1 = 3   | 3-1 = 2
4       5       2        # 9-4 = 5   | 5-3 = 2
9       7       2        # ...
16      9       2
25      11      2

相同的多项式（x^2），但是采用步长为3的差分。非2的幂有助于显示步长因子/幂与自然出现的2的因子之间的区别。

# for stride of 3, printing in groups. A=1, B=0, C=0
poly(i)  1st   2nd  difference from this poly(i) to poly(i+3)
0        9
1       15
4       21

9       27      18     # 36- 9 = 27 | 27-9  = 18
16      33      18     # 49-16 = 33 | 33-15 = 18
25      39      18     # ...

36      45      18     # 81-36 = 45 | 45-27 = 18
49      51      18
64      57      18

81      63      18
100     69      18
121     75      18

Y[]和Z[]的初始化器

  • 初始Y[j] = poly(j)因为它必须存储到相应位置的输出中（data[i+j] = Y[j]）。

  • 初始Z[j]将被添加到Y[j]中，并需要使其成为poly(j+stride)。因此，初始Z[j] = poly(j+stride) - Y[j]，我们可以通过代数化简来简化它。 （对于编译时常量A、B、C，编译器将以任何一种方式进行常量传播。）

    Z[j]保存了在穿过poly(x)的poly(0..stride-1)的起始点时的步幅中的一阶差异。这是上表中的中间列。

  • 必要的更新Z[j] += second_difference是一个标量常量，因为我们可以看到二阶差异是相同的。

    通过尝试几个不同的stride和A值（i ^ 2的系数），我们可以看到它是A * 2 * (stride * stride)。（使用非互质值如3和5有助于解开纷乱的事情。）通过更多的代数，您可以符号地显示这一点。从微积分的角度来看，2的因子是有意义的：d(A*x^2)/dx = 2Ax，而第二个导数是2A。

// Tested and correct for a few stride and coefficient values.

#include <stdalign.h>
#include <stdlib.h>
#define LEN 1024
alignas(64) double data[LEN];

//static const double A = 1, B = 0, C = 0; // for easy testing
static const double A = 5, B = 3, C = 7; // can be function args

void compute2(double * const __restrict__ data)
{
    const int stride = 16; // unroll factor.  1 reduces to the original
    const double diff2 = (stride * stride) * 2 * A; // 2nd-order differences
    double Z[stride], Y[stride];
    for (int j = 0 ; j<stride ; j++){ // this loop will fully unroll
          Y[j] = j*j*A + j*B + C; // poly(j) starting values to increment
        //Z[j] = (j+stride)*(j+stride)*A + (j+stride)*B + C - Y[j];
        //Z[j] = 2*j*stride*A + stride*stride*A + stride*B;
          Z[j] = ((2*j + stride)*A + B)*stride; // 1st-difference to next Y[j], from this to the next i
    }

    for(ptrdiff_t i=0; i < LEN - (stride-1); i+=stride) {
        // loops that are easy(?) for a compiler to roll up into some SIMD vectors
        for (int j=0 ; j<stride ; j++)  data[i+j] = Y[j];  // store
        for (int j=0 ; j<stride ; j++)  Y[j] += Z[j];      // add
        for (int j=0 ; j<stride ; j++)  Z[j] += diff2;     // add
    }

    // cleanup for the last few i values
    for (int j = 0 ; j < LEN % stride ; j++) {
        // let the compiler see LEN%stride to help it decide *not* to auto-vectorize this part
        //size_t i = LEN - (stride-1) + j;
        //data[i] = poly(i);
    }
}

对于stride=1（不展开）的情况，这些简化为原始值。但对于更大的stride，编译器可以将Y[]和Z[]中的元素保存在少数几个SIMD向量中，因为每个Y[j]只与相应的Z[j]交互。

对于编译器（SIMD）和CPU（流水线执行单元），存在独立于stride的并行依赖链，可以利用其优势，以比原始速度快stride倍的速度运行，直到你受限于SIMD FP-add吞吐量而不是延迟，或者存储带宽如果你的缓冲区不适合L1d。（或者直到编译器失败，并且不能像预期那样展开和向量化这些循环！）

实际编译情况：使用clang优美地编译

(Godbolt编译器探索者) 使用clang14 -O3 -march=skylake -ffast-math，stride=16（每个向量包含4个double）时，clang可以很好地自动向量化。

看起来clang进一步展开了2次，将Z[j] += diff2快捷方式转换为tmp = Z[j] + diff2; / Z[j] += 2*diff2;。这减轻了Z依赖链的压力，只留下Y[j]紧贴着Skylake上的延迟瓶颈。

因此，每个asm循环迭代执行2个8个vaddpd指令和2个4存储操作。循环开销是add + 宏融合的cmp/jne，因此是2个uops。（或者对于全局数组，只有一个add/jne uop，计算从负索引逐渐增加到零；它相对于数组末尾进行索引。）

Skylake以非常接近每个时钟周期1个存储和2个vaddpd的速度运行此操作。这是两者的最大吞吐量。前端只需要跟上略高于每个时钟周期3个uops，但自Core2以来就一直是4宽的。

Sandy Bridge系列中的uop缓存使得这不成问题。（除非您遇到Skylake上的JCC错误，因此我使用了-mbranches-within-32B-boundaries让clang填充指令以避免该问题。）

由于Skylake的vaddpd延迟为4个周期，从stride=16产生的4个依赖链刚好足够保持4个独立操作在进行中。任何时候Y[j]+=不能在它准备好的周期运行，都会创建一个气泡。感谢Clang对Z[]链的额外展开，然后可以提前运行Z[j]+=，因此Z链可以领先。使用最旧的优先调度，它倾向于安定下来，进入一个Yj+= uops没有冲突的状态，显然，因为它在我的Skylake上以全速运行。如果我们可以让编译器仍然为stride=32生成漂亮的汇编代码，那么将留下更多空间，但不幸的是它不会。（以奇数大小为代价进行更多的清理工作。）

Clang奇怪地只有在-ffast-math的情况下才能对此进行向量化。完整基准测试中的模板版本不需要-ffast-math。源代码已经被精心编写为支持SIMD操作，具体表现为数学操作按照源代码顺序执行。（尽管快速数学运算使得clang可以更好地展开Z增量）。
另一种循环编写方式是内部只有一个循环，而不是所有Y操作和所有Z操作。这在下面的基准测试中很好（有时甚至更好），但在这里即使使用-ffast-math也无法进行向量化。让编译器为像这样的非平凡问题生成最优展开的SIMD汇编代码可能会很棘手且不可靠，并且可能需要一些实验。
我在Godbolt上将其包含在#if 0/#else/#endif块内。
// can auto-vectorize better or worse than the other way
// depending on compiler and surrounding code.
for(int i=0; i < LEN - (stride-1); i+=stride) {
    for (int j = 0 ; j<stride ; j++){
        data[i+j] = Y[j];
        Y[j] += Z[j];
        Z[j] += deriv2;
    }
}
我们必须手动选择适当的展开数量。过大的展开因子甚至会使编译器无法看到正在发生的事情，并停止将临时数组保留在寄存器中。例如，32或24对于clang来说是一个问题，但16不是。可能有一些调整选项可以强制编译器展开循环直到某个计数; 对于GCC，有时可以使用这些选项让它在编译时看穿某些东西。
另一种方法是手动矢量化，使用#include 和__m256d Z [4]而不是double Z [16]。但是，此版本可以为其他ISA（例如AArch64）进行矢量化。
大展开因子的其他缺点是在问题大小不是展开的倍数时留下更多的清理工作。（您可以使用compute1策略进行清理，在执行标量之前让编译器将其向量化一两次。）
理论上，使用-ffast-math编译器可以帮你完成这个过程，要么是通过在原始多项式上进行强度降低，要么是看到步幅累加的方式从compute2中。但实际上，这很复杂，需要人类自己来完成。除非有人教给编译器如何寻找和应用类似的模式，并使用步幅的方法来计算！但即使使用-ffast-math，对具有不同误差累积特性的算法进行全面重写可能也是不可取的。(整数不会有任何精度问题，但仍然存在复杂的模式匹配/替换)

实验性能结果:

我在我的桌面电脑上 (i7-6700k) 使用 clang13.0.0 进行了测试。在几种编译器选项 (快速数学运算或非快速数学运算) 和内部循环策略的 #if 0 vs. #if 1 的多种组合下，确实可以每个时钟周期运行 1 个 SIMD 存储。我的基准 / 测试框架基于 @huseyin tugrul buyukisik 的版本，改进了重复可测量数量的方法，在 rdtsc 指令之间进行测试，并使用测试循环来检查多项式的简单计算是否正确。

我还让它补偿了核心时钟频率和 "参考" TSC 读取频率的差异，在我的情况下是 3.9 GHz vs. 4008 MHz。(额定最大 Turbo 是 4.2 GHz，但在 Linux 上使用 EPP = balance_performance 时，它只想要时钟提升到 3.9 GHz。)

Source code on Godbolt: using one inner loop, rather than 3 separate j<16 loops, and not using -ffast-math. Using __attribute__((noinline)) to keep this from inlining into the repeat loop. Some other variations of options and source led to some vpermpd shuffles inside the loop.

以下基准数据来自具有错误的Z[j]初始化程序的先前版本，但其循环汇编代码相同。现在Godbolt链接在计时循环后进行了正确性测试，测试通过。实际性能在我的桌面上仍然相同，每个double略高于0.25个周期，即使没有#if 1 / -ffast-math来允许clang额外展开。

$ clang++ -std=gnu++17 -O3 -march=native -mbranches-within-32B-boundaries poly-eval.cpp -Wall
# warning about noipa, only GCC knows that attribute
$ perf stat --all-user -etask-clock,context-switches,cpu-migrations,page-faults,cycles,instructions,uops_issued.any,uops_executed.thread,fp_arith_inst_retired.256b_packed_double -r10 ./a.out
... (10 runs of the whole program, ending with)
...
0.252295 cycles per data element (corrected from ref cycles to core clocks for i7-6700k @ 3.9 GHz)
0.252109 cycles per data element (corrected from ref cycles to core clocks for i7-6700k @ 3.9 GHz)
xor=4303
min cycles per data = 0.251868

Performance counter stats for './a.out' (10 runs):

           298.92 msec task-clock                #    0.989 CPUs utilized            ( +-  0.49% )
                0      context-switches          #    0.000 /sec
                0      cpu-migrations            #    0.000 /sec
              129      page-faults               #  427.583 /sec                     ( +-  0.56% )
    1,162,430,637      cycles                    #    3.853 GHz                      ( +-  0.49% )  # time spent in the kernel for system calls and interrupts isn't counted, that's why it's not 3.90 GHz
    3,772,516,605      instructions              #    3.22  insn per cycle           ( +-  0.00% )
    3,683,072,459      uops_issued.any           #   12.208 G/sec                    ( +-  0.00% )
    4,824,064,881      uops_executed.thread      #   15.990 G/sec                    ( +-  0.00% )
    2,304,000,000      fp_arith_inst_retired.256b_packed_double # 7.637 G/sec

          0.30210 +- 0.00152 seconds time elapsed (+- 0.50%)

fp_arith_inst_retired.256b_packed_double用于计算每个FP加法或乘法指令（FMA为2），因此整个程序中，包括打印等，我们每个时钟周期得到1.98个vaddpd指令。这非常接近理论最大值2/clock，显然没有受到次优的uop调度的影响。（我增加了重复循环，使程序在大部分时间内都在那里，从而使perf stat对整个程序有用。）

这种优化的目标是用更少的FLOPS完成相同的工作，但这也意味着我们基本上在不使用FMA的情况下达到了Skylake的8 FLOP/clock的极限（单核心在3.9 GHz时为30.58 GFLOP/s）。

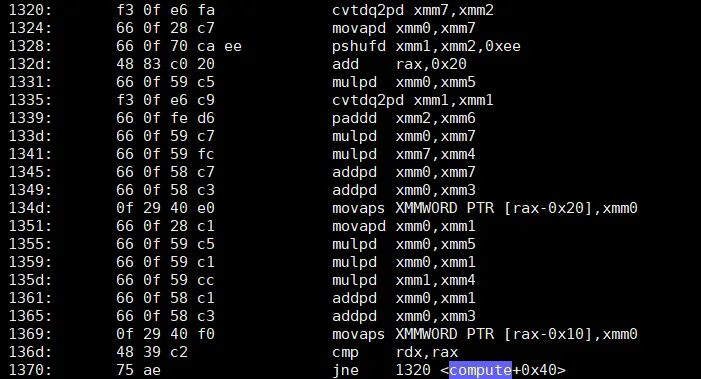
非内联函数的汇编（objdump -drwC -Mintel）; clang使用了4个Y,Z对的YMM向量，并将循环展开了3倍，使其成为24 KiB大小的精确倍数，没有清除操作。请注意，add rax,0x30每次迭代执行3 * stride=0x10个double。

0000000000001440 <void compute2<3072>(double*)>:
# just loading constants; the setup loop did fully unroll and disappear
    1440:  c5 fd 28 0d 18 0c 00 00         vmovapd ymm1,YMMWORD PTR [rip+0xc18]    # 2060 <_IO_stdin_used+0x60>
    1448:  c5 fd 28 15 30 0c 00 00         vmovapd ymm2,YMMWORD PTR [rip+0xc30]    # 2080
    1450:  c5 fd 28 1d 48 0c 00 00         vmovapd ymm3,YMMWORD PTR [rip+0xc48]    # 20a0
    1458:  c4 e2 7d 19 25 bf 0b 00 00      vbroadcastsd ymm4,QWORD PTR [rip+0xbbf] # 2020
    1461:  c5 fd 28 2d 57 0c 00 00         vmovapd ymm5,YMMWORD PTR [rip+0xc57]    # 20c0
    1469:  48 c7 c0 d0 ff ff ff    mov    rax,0xffffffffffffffd0
    1470:  c4 e2 7d 19 05 af 0b 00 00      vbroadcastsd ymm0,QWORD PTR [rip+0xbaf] # 2028
    1479:  c5 fd 28 f4             vmovapd ymm6,ymm4 # buggy Z[j] initialization in this ver used the same value everywhere
    147d:  c5 fd 28 fc             vmovapd ymm7,ymm4
    1481:  c5 7d 28 c4             vmovapd ymm8,ymm4
    1485:  66 66 2e 0f 1f 84 00 00 00 00 00        data16 cs nop WORD PTR [rax+rax*1+0x0]

# top of outer loop.  The NOP before this is to align it.
    1490:  c5 fd 11 ac c7 80 01 00 00      vmovupd YMMWORD PTR [rdi+rax*8+0x180],ymm5
    1499:  c5 d5 58 ec             vaddpd ymm5,ymm5,ymm4
    149d:  c5 dd 58 e0             vaddpd ymm4,ymm4,ymm0
    14a1:  c5 fd 11 9c c7 a0 01 00 00      vmovupd YMMWORD PTR [rdi+rax*8+0x1a0],ymm3
    14aa:  c5 e5 58 de             vaddpd ymm3,ymm3,ymm6
    14ae:  c5 cd 58 f0             vaddpd ymm6,ymm6,ymm0
    14b2:  c5 fd 11 94 c7 c0 01 00 00      vmovupd YMMWORD PTR [rdi+rax*8+0x1c0],ymm2
    14bb:  c5 ed 58 d7             vaddpd ymm2,ymm2,ymm7
    14bf:  c5 c5 58 f8             vaddpd ymm7,ymm7,ymm0
    14c3:  c5 fd 11 8c c7 e0 01 00 00      vmovupd YMMWORD PTR [rdi+rax*8+0x1e0],ymm1
    14cc:  c5 bd 58 c9             vaddpd ymm1,ymm8,ymm1
    14d0:  c5 3d 58 c0             vaddpd ymm8,ymm8,ymm0
    14d4:  c5 fd 11 ac c7 00 02 00 00      vmovupd YMMWORD PTR [rdi+rax*8+0x200],ymm5
    14dd:  c5 d5 58 ec             vaddpd ymm5,ymm5,ymm4
    14e1:  c5 dd 58 e0             vaddpd ymm4,ymm4,ymm0
    14e5:  c5 fd 11 9c c7 20 02 00 00      vmovupd YMMWORD PTR [rdi+rax*8+0x220],ymm3
    14ee:  c5 e5 58 de             vaddpd ymm3,ymm3,ymm6
    14f2:  c5 cd 58 f0             vaddpd ymm6,ymm6,ymm0
    14f6:  c5 fd 11 94 c7 40 02 00 00      vmovupd YMMWORD PTR [rdi+rax*8+0x240],ymm2
    14ff:  c5 ed 58 d7             vaddpd ymm2,ymm2,ymm7
    1503:  c5 c5 58 f8             vaddpd ymm7,ymm7,ymm0
    1507:  c5 fd 11 8c c7 60 02 00 00      vmovupd YMMWORD PTR [rdi+rax*8+0x260],ymm1
    1510:  c5 bd 58 c9             vaddpd ymm1,ymm8,ymm1
    1514:  c5 3d 58 c0             vaddpd ymm8,ymm8,ymm0
    1518:  c5 fd 11 ac c7 80 02 00 00      vmovupd YMMWORD PTR [rdi+rax*8+0x280],ymm5
    1521:  c5 d5 58 ec             vaddpd ymm5,ymm5,ymm4
    1525:  c5 dd 58 e0             vaddpd ymm4,ymm4,ymm0
    1529:  c5 fd 11 9c c7 a0 02 00 00      vmovupd YMMWORD PTR [rdi+rax*8+0x2a0],ymm3
    1532:  c5 e5 58 de             vaddpd ymm3,ymm3,ymm6
    1536:  c5 cd 58 f0             vaddpd ymm6,ymm6,ymm0
    153a:  c5 fd 11 94 c7 c0 02 00 00      vmovupd YMMWORD PTR [rdi+rax*8+0x2c0],ymm2
    1543:  c5 ed 58 d7             vaddpd ymm2,ymm2,ymm7
    1547:  c5 c5 58 f8             vaddpd ymm7,ymm7,ymm0
    154b:  c5 fd 11 8c c7 e0 02 00 00      vmovupd YMMWORD PTR [rdi+rax*8+0x2e0],ymm1
    1554:  c5 bd 58 c9             vaddpd ymm1,ymm8,ymm1
    1558:  c5 3d 58 c0             vaddpd ymm8,ymm8,ymm0
    155c:  48 83 c0 30             add    rax,0x30
    1560:  48 3d c1 0b 00 00       cmp    rax,0xbc1
    1566:  0f 82 24 ff ff ff       jb     1490 <void compute2<3072>(double*)+0x50>
    156c:  c5 f8 77                vzeroupper
    156f:  c3                      ret

相关:

2
@huseyintugrulbuyukisik：更新了来自我的Skylake台式机的测试结果：它每个时钟周期可以运行1个存储器（和两个vaddpd），因此我在没有AVX-512的情况下得到了0.251个元素每个周期的循环次数（我的台式机没有AVX-512）。在测试过程中，我注意到您正在使用rdtsc数字而不是核心时钟周期，这是一个很大的假设。对于某些Xeon处理器，当运行“重型”512位指令时，实际的核心时钟频率接近TSC频率，但这是一个冒险的假设。 - Peter Cordes
2
但无论如何，假设使用ZMM向量的汇编与我的相同，也可以在Skylake-avx512 CPU上每个时钟运行1次存储，因此大约为每个元素0.125个周期。让编译器生成这样的汇编可能会有问题，除非有覆盖调整启发式的选项，因此如果您不使用内部函数，则存在潜在的实际问题。 - Peter Cordes
2
@huseyintugrulbuyukisik：我们并不知道您的代码最终运行在服务器实例的CPU频率上，尽管我们可以使用CPUID获取品牌字符串并打印出来，这可能包括股票“额定”频率。有了这个，就可以进行手动计算（或更正RDTSC猜测数字）。也许采用Quick-bench的策略，通过计时NOP循环来估计当前CPU频率，尽管运行AVX-512“重型”指令的Turbo降低使这更加困难。 - Peter Cordes
2
这只是一个理论问题，没有必要为了实际优化而过于疯狂，只要概念证明就可以了。因此，除非在特定项目中出现真实的用例来指导我们使用哪个编译器/选项、调整哪些问题规模以及如何调用它等方面，否则我不会再花更多时间让它从普通的C++源代码自动向量化。 - Peter Cordes
2
@huseyintugrulbuyukisik：是的，即使在算法的先前版本中，对于许多情况都是正确的。除非你想在瓶颈为ALU吞吐量的循环中多次重新读取它，否则可能值得保留。(特别是如果你可以缓存块它，这样你就不会在全系统内浪费内存带宽，或者L3或L2带宽，如果你的其他循环也需要它的话。) - Peter Cordes
显示剩余17条评论
12

如果您需要这段代码运行得更快，或者您感到好奇，可以尝试以下方法：

把 a[i] = f(i) 的计算方式改为两个加法。将其修改为使用两个加法计算 a[4i] = f(4i)，使用两个加法计算 a[4i+1] = f(4i+1)，以此类推。现在您有四个计算可以并行完成。

编译器很可能会进行相同的循环展开和向量化，并且具有相同的延迟，但是针对的是四个操作而不是一个。

10

如果只使用加法作为优化，那么您将错过新CPU的乘法管道中所有GFLOPS，循环依赖会使自动向量化变得更糟。如果自动向量化，则比乘法+加法快得多。每个数据更节能（仅添加比乘法+添加更好）。

另一个问题是数组末尾由于累计的加法数量而接收到更多舍入误差。但直到非常大的数组才会出现这种情况（除非数据类型变成浮点数）。

当您使用GCC构建选项（在新的CPU上）-std=c++20 -O3 -march=native -mavx2 -mprefer-vector-width=256 -ftree-vectorize -fno-math-errno应用Horner's scheme时，

void f(double * const __restrict__ data){
    double A=1.1,B=2.2,C=3.3;
    for(int i=0; i<1024; i++) {
        double id = double(i);
        double result =  A;
        result *=id;
        result +=B;
        result *=id;
        result += C;
        data[i] = result;
    }
}

编译器会生成以下内容：

.L2:
    vmovdqa ymm0, ymm2
    vcvtdq2pd       ymm1, xmm0
    vextracti128    xmm0, ymm0, 0x1
    vmovapd ymm7, ymm1
    vcvtdq2pd       ymm0, xmm0
    vmovapd ymm6, ymm0
    vfmadd132pd     ymm7, ymm4, ymm5
    vfmadd132pd     ymm6, ymm4, ymm5
    add     rdi, 64
    vpaddd  ymm2, ymm2, ymm8
    vfmadd132pd     ymm1, ymm3, ymm7
    vfmadd132pd     ymm0, ymm3, ymm6
    vmovupd YMMWORD PTR [rdi-64], ymm1
    vmovupd YMMWORD PTR [rdi-32], ymm0
    cmp     rax, rdi
    jne     .L2
    vzeroupper
    ret

使用-mavx512f -mprefer-vector-width=512:

.L2:
    vmovdqa32       zmm0, zmm3
    vcvtdq2pd       zmm4, ymm0
    vextracti32x8   ymm0, zmm0, 0x1
    vcvtdq2pd       zmm0, ymm0
    vmovapd zmm2, zmm4
    vmovapd zmm1, zmm0
    vfmadd132pd     zmm2, zmm6, zmm7
    vfmadd132pd     zmm1, zmm6, zmm7
    sub     rdi, -128
    vpaddd  zmm3, zmm3, zmm8
    vfmadd132pd     zmm2, zmm5, zmm4
    vfmadd132pd     zmm0, zmm5, zmm1
    vmovupd ZMMWORD PTR [rdi-128], zmm2
    vmovupd ZMMWORD PTR [rdi-64], zmm0
    cmp     rax, rdi
    jne     .L2
    vzeroupper
    ret

所有浮点数运算都采用“打包”向量形式，且由于乘加合并为单个FMA，指令更少（这是双倍展开版本）。每64字节数据16条指令（如果使用AVX-512则为128字节）。

霍纳方案的另一个好处是，在FMA指令内精度略高，每个循环迭代仅需要O(1)操作，因此在处理更长的数组时不会积累太多误差。

我认为 Agner Fog 优化手册中的优化应该来自 Quake III 快速逆平方根近似 的时代，当时只有x87才有意义，但现在已被SSE淘汰。那时，SIMD还没有足够宽广的影响，并且对于 sqrt() 和除法而言速度较慢，但具有 rsqrtss 操作。该手册显示版权为2004年，因此有一些搭载 SSE 而非FMA的赛扬CPU。第一款AVX台式机CPU推出得晚得多，FMA甚至比那更晚。

这是另一种使用弱化技术（用于id值）的版本：

void f(double * const __restrict__ data){

    double B[]={2.2,2.2,2.2,2.2,2.2,2.2,2.2,2.2,
    2.2,2.2,2.2,2.2,2.2,2.2,2.2,2.2};
    double C[]={3.3,3.3,3.3,3.3,3.3,3.3,3.3,3.3,
    3.3,3.3,3.3,3.3,3.3,3.3,3.3,3.3};
    double id[] = {0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15};
    for(long long i=0; i<1024; i+=16) {
        double result[]={1.1,1.1,1.1,1.1,1.1,1.1,1.1,1.1,
                        1.1,1.1,1.1,1.1,1.1,1.1,1.1,1.1};
        // The same thing, just with explicit auto-vectorization help
        for(int j=0;j<16;j++)
        {
            result[j] *=id[j];
            result[j] +=B[j];
            result[j] *=id[j];
            result[j] += C[j];
            data[i+j] = result[j];
        }

        // strength reduction
        for(int j=0;j<16;j++)
        {
            id[j] += 16.0;
        }
    }
}

汇编语言:

.L2:
    vmovapd zmm3, zmm0
    vmovapd zmm2, zmm1
    sub     rax, -128
    vfmadd132pd     zmm3, zmm6, zmm7
    vfmadd132pd     zmm2, zmm6, zmm7
    vfmadd132pd     zmm3, zmm5, zmm0
    vfmadd132pd     zmm2, zmm5, zmm1
    vaddpd  zmm0, zmm0, zmm4
    vaddpd  zmm1, zmm1, zmm4
    vmovupd ZMMWORD PTR [rax-128], zmm3
    vmovupd ZMMWORD PTR [rax-64], zmm2
    cmp     rdx, rax
    jne     .L2
    vzeroupper
    ret

当数据，A、B和C数组通过alignas(64)对齐，并且数据数组大小足够小时，它的运行速度为每个元素0.26个周期。

4
询问者只测试了 Nehalem 和 Sandybridge Xeon CPU，它们不支持FMA。您忘记提及使用的构建选项，以使其可以通过AVX2 + FMA自动向量化。但是，如果您拥有FMA，这是一种很好的策略。即使在没有FMA的CPU上，在其中“mulpd”运行在与“addpd”不同的端口上，因此它们只竞争前端吞吐量的情况下，可能也是如此。如果您只关心速度而不是准确性，则gnasher答案中建议的策略（我先前在评论中建议过）使用多个累加器来隐藏FP延迟，可能仍然更好，避免int-> FP成本。 - Peter Cordes
1
正确，存在int->FP成本，并且无法通过积极展开来隐藏。也许最好使用std::memcpy表示一些魔术而不是强制转换。如果循环计数小于53位，则应该起作用。 - huseyin tugrul buyukisik
1
每个结果向量的3个FP数学运算意味着理论最佳情况下，具有2 /时钟FP数学吞吐量的“3 ops * 0.5c/op / 8个元素每个ZMM向量”=每个元素0.1875个周期。但还有两个（被消除的）vmovapd指令和两个存储器，因此这填满了Skylake-X上的整个4宽管道；只有Ice Lake的更宽管道也可以运行循环开销。但是，Ice Lake禁用了mov消除（至少对于整数，我忘记了SIMD），因此这些vmovapd指令将与FMAs竞争。 - Peter Cordes
1
当然，你代码中的瓶颈是 vaddpd 的延迟为4个周期（SKX或ICX，仅在Alder Lake下降到3个周期）。需要更多展开来隐藏当前CPU上的延迟；你只在这里展开了2个ZMM向量。（当然，输出数组应该适合L1d缓存，因为你需要每1.5个时钟周期存储到它，每3个FP数学运算操作=每1.5个周期一个结果向量）具有1.5个时钟周期的所需吞吐量（对于vaddpd）的4个周期延迟需要至少展开4/1.5 = 2.666。所以最好做4个展开。 - Peter Cordes
1
关于功耗的问题 - 一次浮点数加法应该比一次浮点数乘法消耗更少的能量。由于需要将尾数对齐，浮点数加法存在延迟，但是与52位尾数乘法器相比，移位器开关的晶体管数量要少得多。这可能会在执行单元之外的uop调度和其他方面产生相当大的影响。所以我之前对功耗的猜测可能不准确，尽管相比工作负载的变化，CPU因为代码较慢而处于休眠状态与唤醒状态可能会产生更大的差异，这个猜测可能是合理的近似值。 - Peter Cordes
显示剩余20条评论
9

相比加法运算，乘法在我们的CPU中速度较慢。

历史上这可能是真的，对于一些简单低功耗的CPU可能仍然如此，但如果CPU设计者准备“砸门而入”，乘法可以做到与加法几乎同样快。

现代CPU通过流水线和多个执行单元的组合，设计为能够同时处理多个指令。

然而，数据依赖关系是个问题。如果一个指令依赖于另一个指令的结果，那么它的执行不能开始，直到它所依赖的指令完成。

现代CPU使用“乱序执行”来解决这个问题。正在等待数据的指令可被保持排队，而其他指令则可以继续执行。

但即使采取了这些措施，有时CPU仍会简单地无法安排新的任务。

6
Skylake及之后的Intel CPU在Alder Lake之前，对于浮点加/减/乘/混合运算，它们的性能是完全相同的。这些运算都使用相同的2个（完全流水线化）执行端口以及相同的4个时钟周期延迟。而Alder Lake将浮点加/减速度提高到了3个时钟周期，与Haswell相同（但仍然具有与乘法/混合运算相同的每秒2次的吞吐量，不像Haswell）。 - Peter Cordes
3
整数运算方面情况不同，标量整数需要4个时钟周期每个时钟周期执行1次操作，而除法需要3个时钟周期。而在现代英特尔处理器上，SIMD整数的吞吐量是标量整数的4倍。相比旧的CPU，整数乘法仍具有相当高的吞吐量。 - Peter Cordes
3

看起来你既可以拥有蛋糕，也能吃掉它，只需将代码手动并行化，就像这样：

double A4 = A+A+A+A;
double Z = 3A+B;
double Y1 = C;
double Y2 = A+B+C;

int i;
// ... setup unroll when LEN is odd...

for(i=0; i<LEN; i++) {
    data[i] = Y1;
    data[++i] = Y2;
    Y1 += Z;
    Y2 += Z;
    Z += A4;
}

它可能不完全符合编写要求，但你大致了解了：展开循环，以便可以并行处理每个数据相关路径。针对所考虑的机器，四步展开应该可以实现最大性能，但当然，您在软件中硬编码架构时会遇到一些有趣的问题。

1
这就是我的答案，使用了正确的数学方法（除了我没有注意到我们不需要多个Z的副本；只有Y值需要单独的偏移量，所以你发现得很好，这是一个很好的优化）。但无论如何，在询问者的 Nehalem CPU 上至少需要 6 步展开（2 宽 SIMD 和 3 周期延迟 * 1 周期吞吐量 addpd，因此有 6 个标量加法在运行）；在他们的 Sandy Bridge 上需要两倍的数量和 AVX。 - Peter Cordes
1
这实际上不起作用：你需要 Z1，Z2等，而不是所有 Y[j] 共享一个 Z。请参阅我的答案更新；现在它内置了一个正确性测试通过。 - Peter Cordes
网页内容由stack overflow 提供, 点击上面的
可以查看英文原文，
原文链接