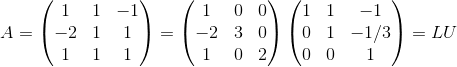Scipy linalg LU分解与我的教科书给出的结果不同

Question

我正在阅读Saul I. Gass的《线性规划》第五版。

他给出了以下文字和示例： “给定一个n x n非奇异矩阵A，则A可以表示为乘积A=LU……如果我们让U（或L）的对角线元素都等于1，则LU分解将是唯一的……”

我使用了从这个SO问题中找到的代码得到可逆的下三角-上三角分解：Is there a built-in/easy LDU decomposition method in Numpy?

但我仍然不知道发生了什么，以及为什么L和U与我的教科书如此不同。有人能向我解释一下吗？

所以这段代码：

import numpy as np
import scipy.linalg as la
a = np.array([[1, 1, -1],
              [-2, 1, 1],
              [1, 1, 1]])
(P, L, U) = la.lu(a)

print(P)
print(L)
print(U)

D = np.diag(np.diag(U))   # D is just the diagonal of U
U /= np.diag(U)[:, None]  # Normalize rows of U
print(P.dot(L.dot(D.dot(U))))    # Check

产生下列输出:

[[ 0.  1.  0.]
 [ 1.  0.  0.]
 [ 0.  0.  1.]]
[[ 1.   0.   0. ]
 [-0.5  1.   0. ]
 [-0.5  1.   1. ]]
[[-2.   1.   1. ]
 [ 0.   1.5 -0.5]
 [ 0.   0.   2. ]]
[[ 1.  1. -1.]
 [-2.  1.  1.]
 [ 1.  1.  1.]]

- Davtho1983

---

你的教科书没有遵循惯例。 - percusse

Answer 1

在矩阵分解中，有一个选择是让哪个矩阵（L 或 U）的对角线为1。教科书上的例子选择了 U，但是scipy的实现选择了L，这就解释了它们之间的差异。

为了说明这一点，我们可以反过来看：

(P, L, U) = la.lu(a.T)

print(P.T)
# [[ 1.  0.  0.]
#  [ 0.  1.  0.]
#  [ 0.  0.  1.]]
print(L.T)
# [[ 1.          1.         -1.        ]
#  [ 0.          1.         -0.33333333]
#  [ 0.          0.          1.        ]]
print(U.T)
# [[ 1.  0.  0.]
#  [-2.  3.  0.]
#  [ 1.  0.  2.]]

通过转置矩阵，我们基本上交换了U和L，使得另一个矩阵在对角线上得到了1。然后，结果与教科书中的相同。请注意，如果置换矩阵P不是单位矩阵，则结果会有所不同。

- MB-F