如何在Python中计算从分布中给定样本列表的值的概率？

Question

不确定这是否属于统计学范畴，但我正在尝试使用Python来实现这一点。我基本上只有一个整数列表：

data = [300,244,543,1011,300,125,300 ... ]

我想知道在这些数据情况下某个数值发生的概率。我使用Matplotlib绘制了这些数据的直方图:

第一个图表示序列中字符的数量，第二个图表示以毫秒为单位的时间量。最小值大于零，但不一定有最大值。这些图是使用数百万个示例创建的，但我不确定能否对分布做出其他假设。我想知道给定几百万个值的情况下新值出现的概率。在第一个图中，我有几百万个不同长度的序列。例如，我想知道长度为200的序列出现的概率。

我知道对于连续分布，任何精确点的概率都应该为零，但是考虑到新值流，我需要能够说明每个值的可能性有多大。我查看了一些numpy/scipy概率密度函数，但我不确定该选择哪个或如何查询新值，一旦我运行类似于scipy.stats.norm.pdf(data)的函数。看起来不同的概率密度函数将以不同的方式适合数据。鉴于直方图的形状，我不确定如何决定使用哪个。

- qazplok11

---

这些数字的性质是什么？它们都是整数吗？有一个固定的范围吗？你能对分布做出任何假设吗（这些数字代表什么）？ - Andrzej Pronobis

考虑到您的数据集，您想要了解什么具体信息？ - juanpa.arrivillaga

在第一张图中，数字代表序列中字符的数量。在第二张图中，它是以毫秒为单位测量的时间量。最小值大于零，但不一定存在最大值。这些图表是使用数百万个示例创建的，但我不确定我能对分布做出任何其他假设。我想知道一个新值的概率，假设我拥有几百万个值的示例。在图1中，我有数百万个不同长度的序列。例如，想知道200个字符长度的概率。 - qazplok11

对于第二个图表，您是否对某些测量时间在某个给定区间内的概率感兴趣？ - juanpa.arrivillaga

@juanpa.arrivillaga 当然可以，你有什么想法？ - qazplok11

Answer 1

由于你似乎没有特定的分布在脑海中，但可能有很多数据样本，我建议使用非参数密度估计方法。 你描述的其中一种数据类型（以毫秒为单位的时间）显然是连续的，而连续随机变量的概率密度函数（PDF）的非参数估计方法之一是直方图，这是你已经提到过的。 然而，如下所示，核密度估计（KDE）可能更好。 你描述的第二种数据类型（序列中的字符数）是离散型的。 在这里，核密度估计也可以很有用，并且可以看作是一种平滑技术，适用于离散变量所有值的样本不足的情况。

估算密度

下面的例子展示了如何首先从两个高斯分布混合中生成数据样本，然后应用核密度估计来找到概率密度函数：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
from sklearn.neighbors import KernelDensity

# Generate random samples from a mixture of 2 Gaussians
# with modes at 5 and 10
data = np.concatenate((5 + np.random.randn(10, 1),
                       10 + np.random.randn(30, 1)))

# Plot the true distribution
x = np.linspace(0, 16, 1000)[:, np.newaxis]
norm_vals = mlab.normpdf(x, 5, 1) * 0.25 + mlab.normpdf(x, 10, 1) * 0.75
plt.plot(x, norm_vals)

# Plot the data using a normalized histogram
plt.hist(data, 50, normed=True)

# Do kernel density estimation
kd = KernelDensity(kernel='gaussian', bandwidth=0.75).fit(data)

# Plot the estimated densty
kd_vals = np.exp(kd.score_samples(x))
plt.plot(x, kd_vals)

# Show the plots
plt.show()

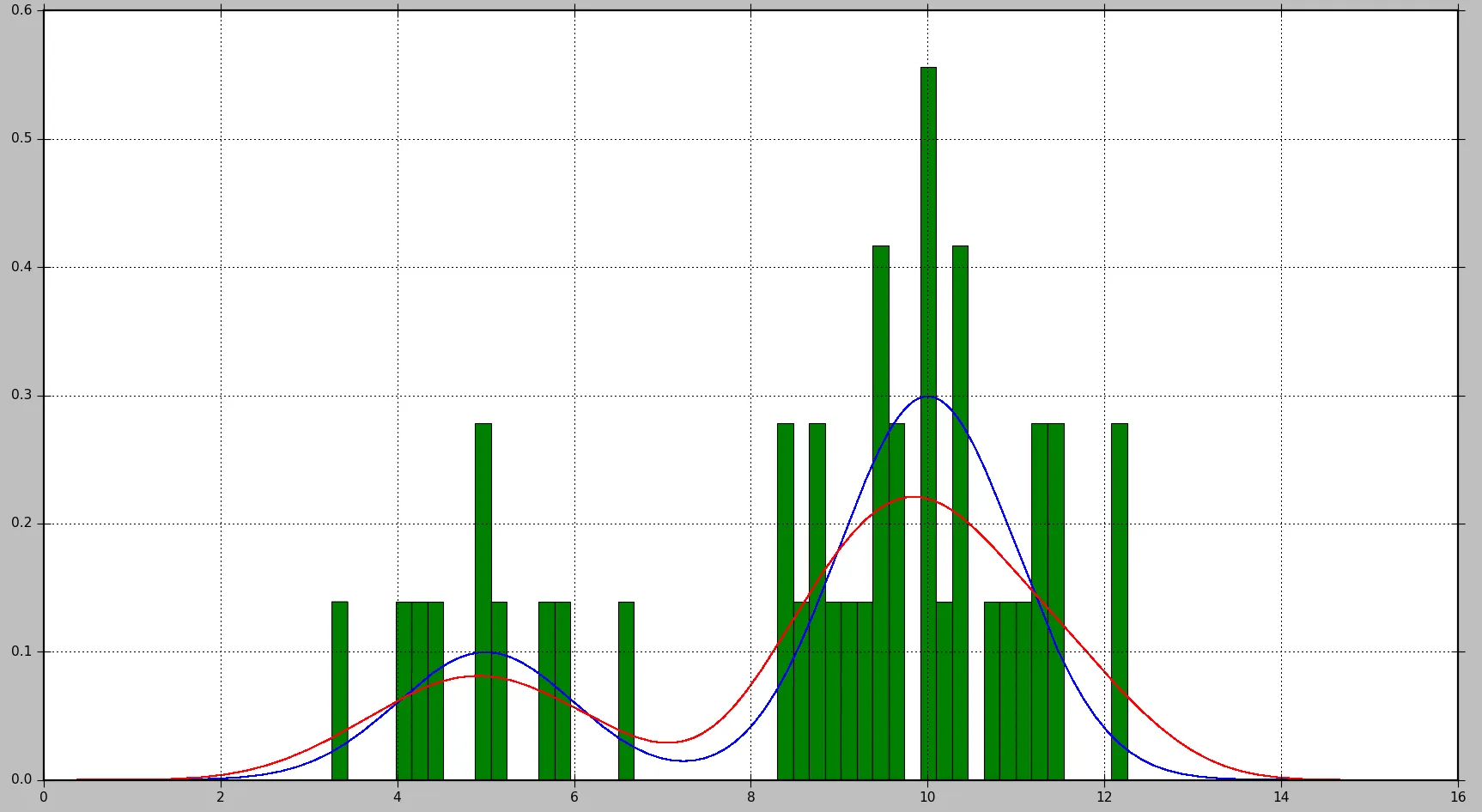
这将生成以下图表，其中真实分布显示为蓝色，直方图显示为绿色，使用KDE估计的PDF显示为红色: 可以看出，在这种情况下，由直方图近似的PDF并不是非常有用，而KDE提供了更好的估计。但是，对于更多的数据样本和适当的bin大小选择，直方图也可能产生良好的估计。

在KDE的情况下，您可以调整的参数是内核(kernel)和带宽(bandwidth)。您可以把kernel视为估计PDF的构建块，在Scikit Learn中提供了几个核函数：高斯(gaussian)、tophat、epanechnikov、指数(exponential)、线性(linear)、余弦(cosine)。改变带宽允许您调整偏差-方差权衡。较大的带宽将导致增加偏差(如果数据样本较少，则效果很好)。较小的带宽将增加方差(估计中包括较少的样本)，但在有更多样本可用时会给出更好的估计。

计算概率

对于PDF，概率是通过计算一定值范围内的积分来获得的。正如您注意到的那样，这将导致特定值的概率为0。

Scikit Learn似乎没有内置的计算概率的函数。但是，在范围内估计PDF的积分很容易。我们可以通过在范围内多次评估PDF并通过每个评估点之间的步长乘以获得的值来进行求和。在下面的示例中，使用步骤(step)获取N个样本。

# Get probability for range of values
start = 5  # Start of the range
end = 6    # End of the range
N = 100    # Number of evaluation points 
step = (end - start) / (N - 1)  # Step size
x = np.linspace(start, end, N)[:, np.newaxis]  # Generate values in the range
kd_vals = np.exp(kd.score_samples(x))  # Get PDF values for each x
probability = np.sum(kd_vals * step)  # Approximate the integral of the PDF
print(probability)

请注意，kd.score_samples 生成数据样本的对数似然。 因此，需要使用 np.exp 来获取似然。

可以使用内置的SciPy集成方法执行相同的计算，这将给出更准确的结果：

from scipy.integrate import quad
probability = quad(lambda x: np.exp(kd.score_samples(x)), start, end)[0]

例如，对于一次运行，第一个方法计算出的概率为0.0859024655305，而第二个方法产生的结果为0.0850974209996139。

- Andrzej Pronobis

---

我之前在研究核密度估计，但是我不太清楚从哪里开始入手。谢谢你提供的详细解释，但是底部的N = 100仍然让我感到困惑。那代表的是样本数量吗？ - qazplok11

我明白了，所以N本质上改变了步长。我理解它在代码中的作用，但不知道数学上如何影响概率。在最后几步中，我们获取每个x的pdf值，将它们乘以步长，然后求和。我不太明白改变N对概率的影响。增加N意味着更多的样本和更小的步长。每个单独的(kd_val * step)更小，但要求和的kd_vals更多。那么积分逼近会发生什么？更准确吗？ - qazplok11

是的，没错，N越大，积分的值就会越精确。 - Andrzej Pronobis

我添加了另一种使用 scipy.integrate.quad 计算积分的方法。这样做会更加方便，而且结果更加准确。 - Andrzej Pronobis

嗨Andrzej，我不明白你如何使用scipy的'quad'。在给定任意大小的1-D数组的情况下，它如何知道“5”和“6”的区间是什么。你能解释一下吗？ - EB88

Quad接受一个函数作为输入（例如示例中的lambda），然后简单地计算该函数在参数（例如5到6之间的值）上的值。 - Andrzej Pronobis

Answer 2

好的，我提供这个作为起点，但是估计密度是一个非常广泛的话题。对于你的情况，涉及序列中字符数量，我们可以从一个简单的频率学家的角度建模，使用经验概率。在这里，概率本质上是百分比概念的概括。在我们的模型中，样本空间是离散的且为所有正整数。那么，你只需计算发生的次数并除以总事件数即可获得概率的估计值。在任何我们没有观测到的地方，我们对概率的估计值为零。

>>> samples = [1,1,2,3,2,2,7,8,3,4,1,1,2,6,5,4,8,9,4,3]
>>> from collections import Counter
>>> counts = Counter(samples)
>>> counts
Counter({1: 4, 2: 4, 3: 3, 4: 3, 8: 2, 5: 1, 6: 1, 7: 1, 9: 1})
>>> total = sum(counts.values())
>>> total
20
>>> probability_mass = {k:v/total for k,v in counts.items()}
>>> probability_mass
{1: 0.2, 2: 0.2, 3: 0.15, 4: 0.15, 5: 0.05, 6: 0.05, 7: 0.05, 8: 0.1, 9: 0.05}
>>> probability_mass.get(2,0)
0.2
>>> probability_mass.get(12,0)
0

现在，针对您的时间数据，将其建模为连续分布会更自然一些。与假设您的数据遵循某个分布并将该分布拟合到您的数据的参数化方法不同，您应采用非参数化方法。一种简单直接的方法是使用核密度估计。您可以将其简单地理解为一种平滑直方图以给您一个连续概率密度函数的方法。有几个库可供使用。对于一元数据，可能最简单的是scipy：

>>> import scipy.stats
>>> kde = scipy.stats.gaussian_kde(samples)
>>> kde.pdf(2)
array([ 0.15086911])

获取某个区间内观测值的概率：

>>> kde.integrate_box_1d(1,2)
0.13855869478828692

- juanpa.arrivillaga

Answer 3

这里有一种可能的解决方案。您可以计算原始列表中每个值出现的次数。给定值的未来概率是其过去出现率，即过去出现次数除以原始列表的长度。在Python中，这非常简单：

x是给定值的列表

from collections import Counter
c = Counter(x)

def probability(a):
    # returns the probability of a given number a
    return float(c[a]) / len(x)

- Paul Cornelius