我知道特征向量仅定义为多个可乘常数。据我所见,所有的numpy算法(例如linalg.eig、linalg.eigh、linalg.svd)对于实矩阵产生相同的特征向量,因此它们显然使用相同的标准化方法。但是,在复杂矩阵的情况下,这些算法会产生不同的结果。也就是说,特征向量相同,只是存在一个(复)常数z。在尝试了eig和eigh后,我发现eigh总是将每个特征向量的第一个分量的相位角度(定义为arctan(虚部/实部))设置为0,而eig似乎从某种(任意?)非零相位角度开始。问:是否有一种方法可以使eigh中的特征向量标准化方式与eig相同(即不强制相位角= 0)?
示例
我有一个复共轭矩阵G,想要使用以下两种算法计算其特征向量:
numpy.linalg.eig:用于真实/ 复正方形矩阵 numpy.linalg.eigh:用于真实对称/ 复共轭矩阵(1.的特殊情况)
检查G是否为共轭。
示例
我有一个复共轭矩阵G,想要使用以下两种算法计算其特征向量:
numpy.linalg.eig:用于真实/ 复正方形矩阵 numpy.linalg.eigh:用于真实对称/ 复共轭矩阵(1.的特殊情况)
检查G是否为共轭。
# check if a matrix is hermitian
def isHermitian(a, rtol=1e-05, atol=1e-08):
return np.allclose(a, a.conjugate().T, rtol=rtol, atol=atol)
print('G is hermitian:', isHermitian(G))
Out:
G is hermitian: True
进行特征分析
# eigenvectors from EIG()
l1,u1 = np.linalg.eig(G)
idx = np.argsort(l1)[::-1]
l1,u1 = l1[idx].real,u1[:,idx]
# eigenvectors from EIGH()
l2,u2 = np.linalg.eigh(G)
idx = np.argsort(l2)[::-1]
l2,u2 = l2[idx],u2[:,idx]
检查特征值
print('Eigenvalues')
print('eig\t:',l1[:3])
print('eigh\t:',l2[:3])
输出:
Eigenvalues
eig : [2.55621629e+03 3.48520440e+00 3.16452447e-02]
eigh : [2.55621629e+03 3.48520440e+00 3.16452447e-02]
两种方法产生相同的特征向量。
检查特征向量
现在看一下特征向量(例如第三个特征向量),它们只是一个常数因子z的差别。
multFactors = u1[:,2]/u2[:,2]
if np.count_nonzero(multFactors[0] == multFactors):
print("All multiplication factors are same:", multFactors[0])
else:
print("Multiplication factors are different.")
输出:
All multiplication factors are same: (-0.8916113627685007+0.45280147727156245j)
检查相位角
现在检查第一个3.特征向量分量的相位角:
print('Phase angel (in PI) for first point:')
print('Eig\t:',np.arctan2(u1[0,2].imag,u1[0,2].real)/np.pi)
print('Eigh\t:',np.arctan2(u2[0,2].imag,u2[0,2].real)/np.pi)
输出:
Phase angel (in PI) for first point:
Eig : 0.8504246311627189
Eigh : 0.0
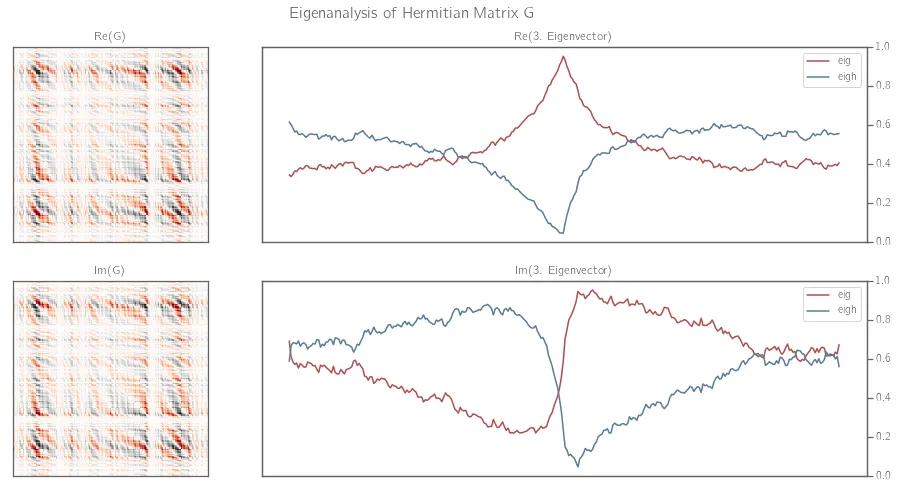
重现该图的代码
num = 2
fig = plt.figure()
gs = gridspec.GridSpec(2, 3)
ax0 = plt.subplot(gs[0,0])
ax1 = plt.subplot(gs[1,0])
ax2 = plt.subplot(gs[0,1:])
ax3 = plt.subplot(gs[1,1:])
ax2r= ax2.twinx()
ax3r= ax3.twinx()
ax0.imshow(G.real,vmin=-30,vmax=30,cmap='RdGy')
ax1.imshow(G.imag,vmin=-30,vmax=30,cmap='RdGy')
ax2.plot(u1[:,num].real,label='eig')
ax2.plot((u2[:,num]).real,label='eigh')
ax3.plot(u1[:,num].imag,label='eig')
ax3.plot((u2[:,num]).imag,label='eigh')
for a in [ax0,ax1,ax2,ax3]:
a.set_xticks([])
a.set_yticks([])
ax0.set_title('Re(G)')
ax1.set_title('Im(G)')
ax2.set_title('Re('+str(num+1)+'. Eigenvector)')
ax3.set_title('Im('+str(num+1)+'. Eigenvector)')
ax2.legend(loc=0)
ax3.legend(loc=0)
fig.subplots_adjust(wspace=0, hspace=.2,top=.9)
fig.suptitle('Eigenanalysis of Hermitian Matrix G',size=16)
plt.show()