似乎没有快速的离散余弦变换（DCT），但是在统计包中有一种快速傅里叶变换（FFT），因此以下是如何使用FFT获取快速DCT。
请自行承担风险。我没有进行任何严格的检查。我在几个不同大小的向量上进行了检查，并在其中与dtt包中的函数dct给出了相同的结果。如果有人想通过将其与dct的输出进行比较来对我进行双重检查，请随时这样做并发布您的结果。
将您的向量扩展为两倍长的向量，方法如下：如果您的向量是v =（1,2,3），则将条目加倍为w =（1,2,3,3,2,1）。注意顺序。如果您的向量是v =（1,2,4,9），则将条目加倍为w =（1,2,4,9,9,4,2,1）
让N成为您原始向量的长度（在您将其长度加倍之前）。
然后，.5 * fft（w）/ exp（complex（imaginary = pi / 2 / N）*（seq（2 * N）-1））的前N个系数应该与计算dct（v）相同，除了它在几乎所有情况下都应该更快。
速度考虑。如果您对N进行质因数分解，则计算快速dct所需的时间就像对这些质因数中的每一个执行慢速dct所需的时间一样。因此，如果N是2^K，则相当于在长度为2的向量上执行K个不同的慢速dct变换，因此速度非常快。如果N是质数（最坏情况），则根本没有加速。速度提升最大的是长度为2的幂次方的向量。
注意：上面的R代码看起来非常不友好，所以让我解释一下。在正确的方式下将长度加倍后，您得到的fft的前N个系数几乎是正确的。但是，系数需要进行一些微调。让P代表e^(pi * i / 2 / N)。保持第一个系数不变。将第二个系数除以P，将第三个系数除以P^2，将第四个系数除以P^3，依此类推...然后将所有系数除以2（包括第一个系数），以与R用于dct的归一化一致。
这样做应该与使用dtt软件包中的dct函数相同，但在几乎所有情况下都要快得多。
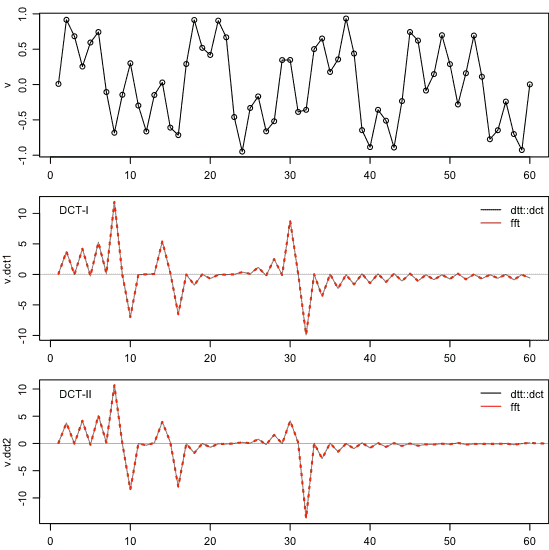
约翰和伊戈尔的答案都是正确的，但我认为他们缺少一些示例代码。
library(dtt)
par(mfrow=c(3, 1), mar=c(2, 3, 1, 0.1), mgp=c(2, 0.8, 0))
set.seed(1)
N <- 60
v <- sin(seq(0, pi*2*4, l=N))/2 +
sin(seq(0, pi*2*7, l=N))/3 +
sin(seq(0, pi*2*15, l=N))/2 +
runif(N, -1, 1)/40 +
runif(N, -1, 1)/40
plot(v, type="o")
DCT-I:
v.dct1 <- dct(v, variant=1)
w <- c(v, v[(N - 1):2])
w.dct1 <- 0.5 * Re(fft(w)[1:N])
plot(v.dct1, type="l", col="#00000088")
abline(h=0, col="#00000044")
lines(w.dct1, col=2, lty=3, lwd=2)
legend("topright", c("dtt::dct", "fft"), bty="n", col=1:2, lwd=1)
legend("topleft", "DCT-I", bty="n")
DCT-II:
v.dct2 <- dct(v, variant=2)
P <- exp(complex(imaginary=pi / 2 / N)*(seq(2*N)-1))
w <- c(v, v[N:1])
w.dct2 <- 0.5 * Re(fft(w)[1:N]/P)
plot(v.dct2, type="l", col="#00000088")
abline(h=0, col="#00000044")
lines(w.dct2, col=2, lty=3, lwd=2)
legend("topright", c("dtt::dct", "fft"), bty="n", col=1:2, lwd=1)
legend("topleft", "DCT-II", bty="n")
0.5 * Re(fft(w) / P)[1:N]吗？当我这样做时，我的结果与dtt::dct一致，但按照原来的向量方式进行计算仍然会加倍。 - tmastny免责声明：我从未使用过dtt包，无法将我的结果与其结果进行比较。我的答案是关于DCT / FFT的通用性。
John的想法是正确的，但他在重复向量方面有误，并且必须通过调整系数（e ^（pi * i / 2 / N）因子）来补偿它。通过正确扩展原始向量，FFT可以直接产生正确的结果（*）。引用自维基百科：
“DCT-I等效于具有偶对称性的2N-2个实数的DFT（最多乘以2的比例因子）。例如，N=5个实数abcde的DCT-I恰好等价于8个实数abcdedcb（偶对称性）的DFT，除以二。”
也就是说，如果我们有一个向量v = [1, 2, 3, 4, 5]，希望对其执行DCT，则应构造一个新向量w = [1, 2, 3, 4, 5, 4, 3, 2]并对其执行FFT。请注意，v的第一个和最后一个分量仅按原始顺序出现一次在w中！
这是因为偶函数（关于零对称的函数）的傅里叶变换仅由实数（余弦）系数组成。如果我们通过包含整个反转的v来构造向量w，如John所建议的那样，它将在-0.5周围对称。由于这个微小的移位，傅里叶变换也会产生虚数（正弦）系数。
（*）此方法产生DCT-I。John的方法似乎旨在获得DCT-II。
library(sos); findFn("fast fourier cosine transform")在wavethresh中揭示了一个rfft函数。看起来它是通过一种打包/解包机制实现的——根据我对 Numerical Recipes 的模糊记忆，这可能可以更有效地完成，但也许它有用呢？ - Ben Bolker