如何检测网格上的正方形，这些正方形在添加障碍后永远不可能成为最短路径的一部分？

Question

我有一个网格，其中包含起点、终点和一些障碍。单位只能沿着最短路径（仅向上/向下/向左/向右移动），从起点到达终点，不能穿过障碍物。

用户可以添加任意数量的额外墙壁来改变路径。

然而，请注意，无论添加多少墙或添加在哪里，总有一些方块永远不可能成为最短路径的一部分！

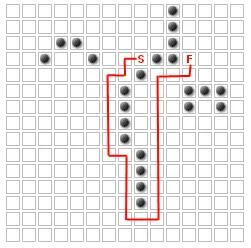
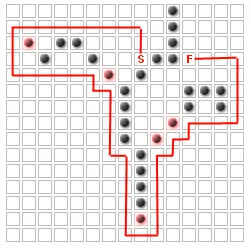
这些方块永远不能成为最短路径的一部分！

我正在寻找一种方法来检测哪些方块永远不可能成为最短路径的一部分。

---

上述案例很容易找到；但还有更复杂的情况。考虑以下内容：

在上面的图像中，带有红点的正方形永远不可能成为最佳路径的一部分，因为该区域只有一个入口，且仅有两个空间宽。如果它是三个空间宽，或者如果任何一个墙被拆除，大多数这些正方形都有可能成为最佳路径的一部分。

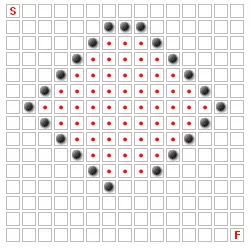
我一直在尝试找出解决此类问题的方法（主要使用min-cuts和flood-fills），但没有成功。有人知道如何解决这个问题吗？

- BlueRaja - Danny Pflughoeft

---

你的两个示例共同具有的一个常见特征是具有大小为1或2的团分离器。你能想到一个不符合这种情况的例子吗？ - krjampani

@jkraju，我还没有想到一个例子，其中死细胞（即不能成为任何最短路径的细胞）没有大小为1或2的分隔符；但是，很容易想到对于非死细胞而言，大小为2的分隔符的例子。 - James Waldby - jwpat7

@jwpat7 我只考虑将 s 和 f 保持在同一组件中的分隔符。也许您考虑的是将 s 与 f 分开的 2-团分隔符？我同意这很容易构造出这样的例子。 - krjampani

Answer 1

考虑从S到F的任何路径。如果您删除每个其他正方形，则该路径可能是最短路径，除非您可以只使用这些瓷砖来“捷径”。当您有两个相邻的正方形不相邻于路径时，这种情况才会发生。因此，您需要考虑所有相邻正方形对；它们断开S或F（而不是将S与F分离）的任何内容都不能成为最短路径的一部分。而且，可以通过单个正方形断开连接的瓷砖也不能成为从S到F的任何路径（不重复顶点），因此它们也需要消失。

令N为网格中正方形的数量。对于任何特定的正方形对（共O(N)个），可以使用floodfill在O(N)时间内计算所断开的内容，因此这是O(N ^ 2)。这比您尝试过的最小割更经济，因此我认为这对您来说足够便宜。

- Jonathan Paulson

---

当时，我接近这个解决方案（请参见@Topro的答案）！我喜欢这两个答案，但我选择了这个答案是因为它提供了有力的证明，说明没有其他情况需要考虑。谢谢你们俩-我现在已经实施了这个解决方案，而且它运行得很好！ - BlueRaja - Danny Pflughoeft

很好的解释方式。我的答案基本上采用了相同的技术，但尝试以O(N)的时间复杂度实现会更加困难。 - Rusty Rob

Answer 2

首先我们可以看到，被一个或两个相邻网格所阻挡的区域永远不会成为任何最短路径。

以你的例子为例，就是那两个黄色网格阻挡了路径。

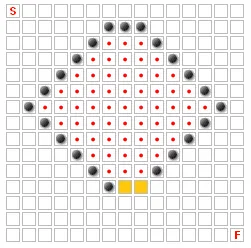
一个格子被阻挡很容易理解。当两个格子被阻挡时：

1. 如果它们不相邻，我们可以添加额外的墙壁使其成为唯一的路径，从其中一个进入，从另一个出来，因此我们可能需要内部的格子。
2. 如果它们相邻，我们总是可以直接从一个格子到达另一个格子，因此我们仍然不需要该区域内部的格子。

因此，这里就有了算法：

枚举每个空格子

1. 在其上放置一堵墙，并使用泛洪填充查找被阻挡的区域，它们没有用处。
2. 尝试在其四个相邻的格子（如果为空）中放置一堵墙，并使用泛洪填充查找被阻挡的区域，它们没有用处。

- iloahz

---

嗯，我认为你说得对*(但我们需要淹没单独的方块，以找到起始不可达的方块。此外，您只需要检查两个邻居，而不是四个)*。在您的图像中，黄色方块可能是最佳路径的一部分，这让我感到困惑了很长时间，但我刚刚意识到，在我们进行淹没填充后，我们不将放置墙壁的两个方块视为不可达区域的一部分。哎呀！ - BlueRaja - Danny Pflughoeft