如何找到可以适合给定正方形的最小正方形的数量？

Question

假设我有一个7x7的正方形。我可以用其他正方形（即1x1，2x2.....6x6的正方形）来填充这个正方形。如何使用最少的小正方形填满整个正方形，请帮我解答。

- user2220890

---

这不够清楚。你能举个例子吗？ - Oliver Charlesworth

请查看whathaveyoutried.com和FAQ http://stackoverflow.com/faq。 - Eric J.

如果我需要填充一个3X3的正方形，那么我可以用9个1x1的正方形来填充它，或者用1个2X2和5个1x1的正方形来填充它。由于第二种选项需要更少的正方形，因此我们可以选择第二种选项。 - user2220890

http://mathworld.wolfram.com/MrsPerkinssQuilt.html - Tom

同一个老师？ :) http://stackoverflow.com/questions/15688161/construct-large-square-using-smaller-sqaures - MBo

如果原始正方形为 n x n（其中 n 总是整数，对吗？）且 n 可以被2整除（即 n 是偶数），则您始终可以将四个 (n/2) x (n/2) 的正方形精确地放入其中。没有一种方法可以将3个或2个正方形拼在一起以制作另一个正方形，因此这解决了所有可能情况的一半问题。 - SGM1

Answer 1

考虑一个边长为s的正方形。从中切出一个边长为m的小正方形，会得到一个边长为m的正方形、一个边长为n的正方形和两个尺寸为m x n的矩形，其中 m + n = s。

当 s 是偶数时，正方形可以被划分，使得 m = n，此时矩形也将是正方形，结果为4。

然而，当s为奇数时，必须选择m和n的值，以便所得到的矩形可以用最少的正方形填充。似乎没有一种立即显而易见的方法来确定最佳配置，因此我建议想出一种算法来找出可以用最少数量的正方形填充m x n大小的矩形（这是一个稍微简单的问题，我相信它可以用递归算法解决）。所需总正方形数将等于2 x ([number of squares in m x n rectangle] + 1)。您可以使用循环来检查1到s/2之间所有m的大小。

希望这能让您开始。

- Otaia

---

不确定计算m x n是否更简单，因为n x n可以被视为它的一种特殊情况。 - lmsteffan

总所需正方形的数量将等于2 x（[m x n矩形中正方形的数量] + 1）。这是不正确的！考虑n = 4，m = 3。您建议在4x4对面放置一个3x3会需要10个较小的正方形，这是不理想的。在对角线相反的角落放置2x2可以将所需数量减少到9个。我认为最好从在nxn的相邻角落中放置mxm正方形开始。 - Klas Lindbäck

嗯，你说得对。这个问题比我想象的要复杂。 - Otaia

Answer 2

首先检查n是否为偶数。如果n是偶数，则答案为4，因为没有一种方法可以将3个正方形或2个正方形拼在一起以制作另一个正方形，因此这解决了所有可能情况的一半。

在继续之前：这种方法不完整，可能是错误的方法

我只是想提出一个非常规的想法，因为我觉得这可能有所帮助，并且希望能够推进问题的解决。我感觉它可能与哥德巴赫猜想有一定的相关性。该算法对于较大的值来说可能过长，而且我不确定有多少优化正在发生。

现在我的想法是尝试枚举所有三元组(n1,n2,n3)，其中n1 + n2 + n3 = n且n1，n2，n3都是素数（均>= 2）且n >= 7且n1 <= n2 <= n3

现在让我详细描述我的算法：

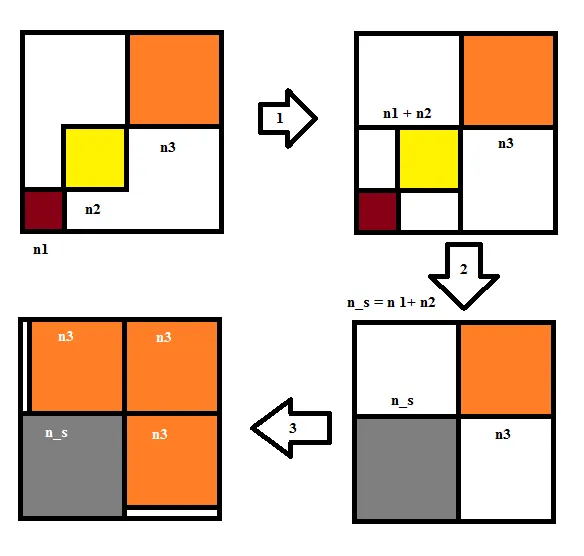
现在我的想法是找到所有可能的三元组(n1，n2，n3)，使其符合上述定义。接下来设置n_s = n1 + n2。如果n_s > n3，就按照上述图像进行操作；否则，交换n_s和n3。

现在的问题是剩下的白色矩形（应该彼此相等）。

让n4 x n3表示矩形，其中：

n4 = n - 2 * n3 \\if following the depicted example

枚举所有可能的三元组 (n41, n42, n43)（将 n 视为 n = n4，因此 n3 >= 7），以及 (n31, n32, n33)（将 n 视为 n = n3，因此 n3 >= 7）。接下来找到 n_s3 == n_s4 的值，并且它们都是它们可能的最大值。
例如：

假设 x3 = 17 和 x4 = 13

  Enumeration of x3 = 17:
  2 + 2 + 13
  3 + 3 + 11
  5 + 5 + 7
  
  Enumeration of x_s3:
  4 = 2 + 2
  6 = 3 + 3
  10 = 5 + 5
  12 = 5 + 7
  14 = 3 + 11
  15 = 2 + 13
  
  Enumeration of x4 = 13:
  2 + 2 + 7
  3 + 5 + 5
  
  Enumeration of x_s4:
  4 = 2 + 2
  8 = 3 + 5
  9 = 2 + 7
  10 = 5 + 5

由于 10 是 13 和 17 之间共享的最大值，因此您可以在（两个矩形中）放置一个 10x10 的正方形，现在您有了一个非平行四边形，这使得填充变得越来越困难，但可能是（我感觉）朝着正确的方向。

欢迎所有反馈。

- SGM1

Answer 3

考虑一个边长为s的正方形。 将s分解成质数。然后针对每个质数sp解决问题。对于sp x sp和s x s，答案将是相同的。最小的质数可能会给出最低的结果。我没有证明这一点，但我手动检查了17 x 17以下的情况。 这是Otaias关于偶数s得到4的概念的推广。

放置算法：

您需要从n =（s + 1）/ 2开始循环，向下取整，直到n = s-1为止。

将n x n正方形放在角落里。

让m = s-n。 将m x m正方形放在相邻的角落里，并继续放置它们，直到它们（几乎）到达n x n正方形的末端。

剩余的空间将是m x m（如果你很幸运），或者是最多2m-1 x 2m-1，缺少一个角落。

使用类似的算法填充剩余的空间。从放置一个n2 x n2的正方形开始，放在缺失角落的对面。

通过手工操作，我获得了以下结果：

s  minimum number of squares:
2   4
3   6
5   8
7   9
11  10
13  11
17  12

- Klas Lindbäck

---

你的结果似乎不正确（你不能用5个正方形覆盖一个3x3的正方形）。即使你修复了这个问题，我也不明白为什么你认为你的算法是最优的。 - interjay

如果我理解正确的话，它甚至没有完全指定：重复这个过程两次后，你会得到一个缺少两个角的正方形，而从那里继续下去并不清楚... - interjay

@interjay 抱歉，打错了，3x3应该是6。你说得对，我的答案不完整。这是我在短时间内思考的结果。我希望其他人能发现它的潜力并进一步改进它。如果你想在合理的时间内解决这种问题，那么任何可以减少暴力破解所需的信息都是有帮助的。 - Klas Lindbäck