优化填充网格图形的正方形

Question

优化填充网格图形的正方形

algorithmoptimizationdynamic-programming

8

最近我设计了一个儿童解谜游戏。然而，我想知道最优解。

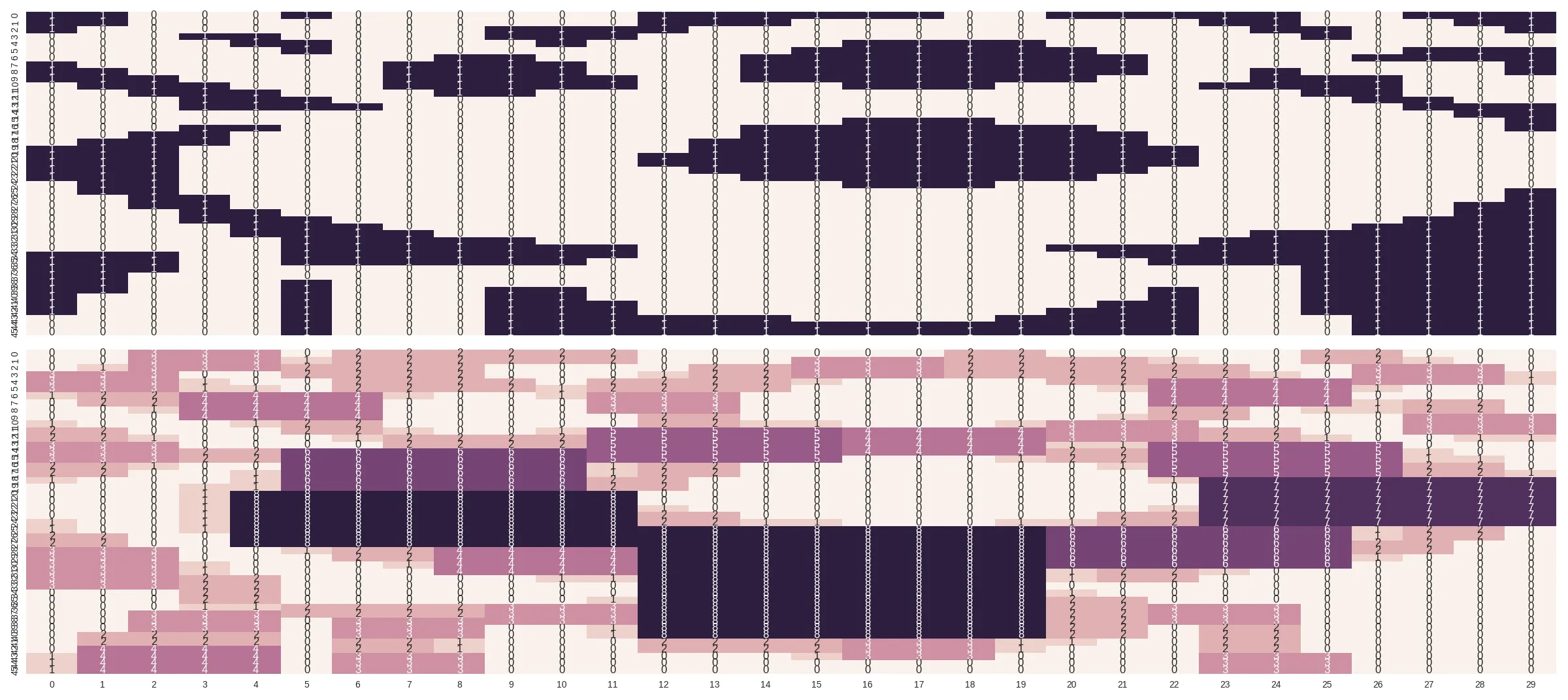
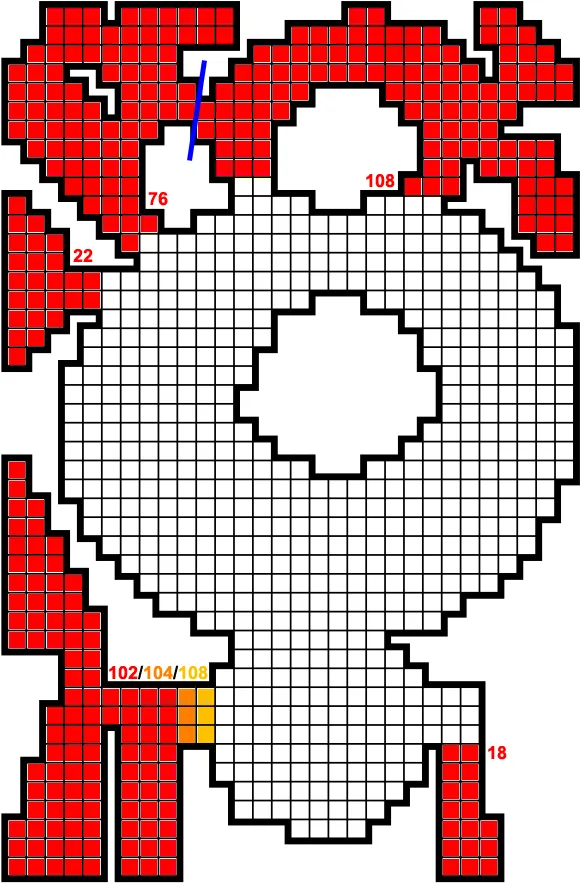
问题如下：你有这样一个由小正方形组成的图案

你必须用较大的正方形填充它，并按以下表格进行评分：

| Square Size | 1x1 | 2x2 | 3x3 | 4x4 | 5x5 | 6x6 | 7x7 | 8x8 |
|-------------|-----|-----|-----|-----|-----|-----|-----|-----|
| Points      | 0   | 4   | 10  | 20  | 35  | 60  | 84  | 120 |

有太多可能的解决方案需要检查。其他人建议使用动态规划，但我不知道如何将图形分成较小的部分，这些部分放在一起具有相同的最优解。

我希望能够找到一种在合理时间内（如在常规桌面上的几天内）找到这类问题最优解的方法。迄今为止，通过猜测算法和一些手动工作找到的最高分数为1112。

欢迎提供类似问题的解决方案，包括组合子问题的解决方案。我不需要所有代码都写出来，一个算法的大纲或想法就足够了。

注意：最大适合的正方形是8x8，因此不包括更大正方形的得分。

[[1,1,0,0,0,1,0,0,0,0,0,0,1,1,1,1,1,1,0,0,1,1,1,1,1,0,0,1,1,1],
 [1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,1,1,0,0,0,1,1],
 [1,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,1],
 [0,0,0,1,1,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0],
 [0,0,0,0,1,1,0,0,0,0,1,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0],
 [0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,1,1,1],
 [0,0,0,0,0,0,0,0,1,1,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,1,1,1,1],
 [1,0,0,0,0,0,0,1,1,1,1,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,1],
 [1,1,0,0,0,0,0,1,1,1,1,0,0,0,1,1,1,1,1,1,1,1,0,0,1,0,0,0,0,1],
 [1,1,1,0,0,0,0,1,1,1,1,1,0,0,1,1,1,1,1,1,1,0,0,0,1,1,1,0,0,0],
 [0,1,1,1,0,0,0,1,1,1,1,1,0,0,0,0,1,1,1,0,0,0,0,1,1,1,1,0,0,0],
 [0,0,1,1,1,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0],
 [0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0],
 [0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1],
 [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1],
 [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,1],
 [0,0,0,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1],
 [0,0,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0],
 [0,1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0],
 [1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0],
 [1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0],
 [1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0],
 [1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0],
 [1,1,1,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0],
 [0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0],
 [0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1],
 [0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1],
 [0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1],
 [0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1],
 [0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1],
 [0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1],
 [0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1],
 [0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1],
 [0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1],
 [1,1,1,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1],
 [1,1,1,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1],
 [1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1],
 [1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1],
 [1,1,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1],
 [1,1,0,0,0,1,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,1,1,1,1],
 [1,0,0,0,0,1,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,1,1,1,1],
 [1,0,0,0,0,1,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,1,1,0,0,1,1,1,1,1],
 [1,0,0,0,0,1,0,0,0,1,1,1,0,0,0,0,0,0,0,0,1,1,1,0,0,1,1,1,1,1],
 [0,0,0,0,0,1,0,0,0,1,1,1,1,1,1,0,0,0,0,1,1,1,1,0,0,0,1,1,1,1],
 [0,0,0,0,0,1,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1],
 [0,0,0,0,0,1,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]];

- Roxor9999

1

能否以某种机器可读格式（例如二进制矩阵）提供上述问题实例的机会？ - sascha

1

刚想提出同样的建议。最好是一个由0和1组成的表格。 - Stormwind

2

由于那肯定是一份工作，我认为这次向@m69表示感谢是完全正确的，来自一个老兵对另一个老兵的感激之情，并代表整个社区。我很快就会开始攻击，使用一个尚未命名的并行计算机语言；-)。我已经有了一个开始的想法，但不知道如何结束。 - Stormwind

没错，这是一个不错的入口点！隔离那些可以无条件优化的分支，使得这些标记对其余部分没有任何影响。为了使开放床变小。编辑：想一想，这可能是一个手动步骤 :-). - Stormwind

我一开始写了一个暴力算法，这样我就有了其他方法比较的结果，但是对于超过几行拼图来说，它速度太慢了。问题是，否则我觉得你找不到最优解。 - m69 ''snarky and unwelcoming''

显示剩余4条评论

3个回答

3

可以将问题重新表述为另一个NP难问题 :-)

创建加权图，其中顶点是可以放置在棋盘上的所有可能的方块，权重与大小有关，边缘位于相交的方块之间。不需要表示1x1的正方形，因为它们的权重为零。

例如，对于简单的空3x3棋盘，有： - 5个顶点：一个3x3和四个2x2， - 7条边：4条在3x3正方形和每个2x2正方形之间，6条在每对2x2正方形之间。

现在的问题是找到最大权独立集。

我对这个主题不是很有经验，但从维基百科的描述中看来，可能存在足够快的算法。这个图不属于已知多项式时间算法的类之一，但它非常接近P5-free图。在我的看来，仅有可能在2x2正方形之间出现P5，这意味着长度为5的宽度为2的条带。左下角有一个。在找到独立集之前，这些区域可以被覆盖（删除），而不会损失最优解或只损失很少。

- Ante

哎呀，谢谢你确认了我的担忧。不幸的是，维基百科上在“P5-free graph”下面没有链接。你知道有没有一个适合初学者理解的好解释？ - m69 ''snarky and unwelcoming''

1

@m69 我也查了一下定义。据我所知，这是一个没有5个顶点诱导子图是路径的图。我在这篇论文中找到了定义。 - Ante

好主意！但是即使现在我们的图形有1810个顶点，我能找到的最佳算法对于最大权独立集合的复杂度比O(1.2^n)还要差一些。所以即使它会快得多，我认为它仍然太慢了。 - Roxor9999

@Roxor9999 你尝试用更小的例子运行它了吗？ - Ante

@Ante 是的，它产生了最优的结果，或者至少是已知的最佳结果。 - Roxor9999

2

(这不是一个完整的答案；我只是分享我正在处理的内容，以便我们可以合作。)

我认为一个很好的第一步是通过给每个单元格赋予最大正方形大小的值来转换二进制网格，就像这样：

0,0,3,2,1,0,3,2,2,2,2,1,0,0,0,0,0,0,2,1,0,0,0,0,0,2,1,0,0,0
0,0,2,2,2,3,3,2,1,1,1,1,0,0,0,3,3,3,3,3,3,2,1,0,0,1,2,1,0,0
0,2,1,1,1,2,3,2,1,0,0,0,0,3,2,2,2,2,2,2,3,3,2,1,0,0,3,2,1,0
3,2,1,0,0,1,3,2,1,0,0,0,3,2,2,1,1,1,1,1,2,3,3,2,1,0,2,2,2,1
3,3,2,1,0,0,2,2,2,1,0,3,2,2,1,1,0,0,0,0,1,2,4,3,2,2,1,1,1,1
2,3,3,2,1,0,2,1,1,1,2,3,2,1,1,0,0,0,0,0,0,1,3,3,2,1,1,0,0,0
1,2,3,4,3,2,1,1,0,0,1,3,2,1,0,0,0,0,0,0,0,0,2,2,2,1,0,0,0,0
0,1,2,3,3,2,1,0,0,0,0,2,2,1,0,0,0,0,0,0,0,0,2,1,1,2,2,2,1,0
0,0,1,2,3,2,1,0,0,0,0,1,2,1,0,0,0,0,0,0,0,0,2,1,0,1,1,2,1,0
0,0,0,1,2,2,1,0,0,0,0,0,2,1,0,0,0,0,0,0,0,2,1,1,0,0,0,3,2,1
1,0,0,0,1,2,1,0,0,0,0,0,4,3,2,1,0,0,0,4,3,2,1,0,0,0,0,2,2,1
2,1,0,0,0,1,2,1,0,0,5,5,4,4,4,4,4,4,4,5,5,4,3,2,1,0,0,1,2,1
3,2,1,0,0,0,1,6,6,5,4,4,4,3,3,3,3,3,3,4,4,5,4,3,2,1,0,0,1,1
3,2,1,0,0,0,0,6,5,5,4,3,3,3,2,2,2,2,2,3,3,4,5,4,3,2,1,0,0,0
3,2,2,2,2,7,6,6,5,4,4,3,2,2,2,1,1,1,1,2,2,3,5,5,4,3,2,1,0,0
2,2,1,1,1,7,6,5,5,4,3,3,2,1,1,1,0,0,0,1,1,2,4,6,5,4,3,2,1,0
2,1,1,0,0,7,6,5,4,4,3,2,2,1,0,0,0,0,0,0,0,1,3,6,5,4,3,2,1,0
1,1,0,0,8,7,6,5,4,3,3,2,1,1,0,0,0,0,0,0,0,0,2,7,6,5,4,3,2,1
1,0,0,0,8,7,6,5,4,3,2,2,1,0,0,0,0,0,0,0,0,0,1,7,6,5,4,3,2,1
0,0,0,7,8,7,6,5,4,3,2,1,1,0,0,0,0,0,0,0,0,0,0,6,6,5,4,3,2,1
0,0,0,6,8,7,6,5,4,3,2,1,0,0,0,0,0,0,0,0,0,0,0,6,5,5,4,3,2,1
0,0,0,5,7,7,6,5,4,3,2,1,0,0,0,0,0,0,0,0,0,0,0,6,5,4,4,3,2,1
0,0,0,4,6,7,7,6,5,4,3,2,1,0,0,0,0,0,0,0,0,0,6,5,5,4,3,3,2,1
0,0,0,3,5,6,7,7,6,5,4,3,2,1,0,0,0,0,0,0,0,6,6,5,4,4,3,2,2,1
1,0,0,2,4,5,6,7,8,7,6,5,4,3,2,1,0,0,0,7,6,6,5,5,4,3,3,2,1,1
1,0,0,1,3,4,5,6,7,7,8,8,8,8,8,8,7,7,6,6,6,5,5,4,4,3,2,2,1,0
2,1,0,0,2,3,4,5,6,6,7,7,8,7,7,7,7,6,6,5,5,5,4,4,3,3,2,1,1,0
2,1,0,0,1,2,3,4,5,5,6,6,8,7,6,6,6,6,5,5,4,4,4,3,3,2,2,1,0,0
3,2,1,0,0,1,2,3,4,4,5,5,8,7,6,5,5,5,5,4,4,3,3,3,2,2,1,1,0,0
3,2,1,0,0,0,1,2,3,3,4,4,8,7,6,5,4,4,4,4,3,3,2,2,2,1,1,0,0,0
4,3,2,1,0,0,0,1,2,2,3,3,8,7,6,5,4,3,3,3,3,2,2,1,1,1,0,0,0,0
3,3,2,1,0,0,0,0,1,1,2,2,8,7,6,5,4,3,2,2,2,2,1,1,0,0,0,0,0,0
2,2,2,2,1,0,0,0,0,0,1,1,8,7,6,5,4,3,2,1,1,1,1,0,0,0,0,0,0,0
1,1,1,2,1,0,0,0,0,0,0,0,8,7,6,5,4,3,2,1,0,0,0,0,0,0,0,0,0,0
0,0,0,2,1,0,0,0,0,0,0,0,8,8,7,6,5,4,3,2,1,0,0,0,0,0,0,0,0,0
0,0,0,2,1,0,0,0,0,0,0,6,8,7,7,6,6,5,4,3,2,1,0,0,0,0,0,0,0,0
0,0,0,2,2,2,3,3,3,3,3,5,7,7,6,6,5,5,4,3,3,3,3,2,1,0,0,0,0,0
0,0,3,2,1,1,3,2,2,2,2,4,6,6,6,5,5,4,4,3,2,2,2,2,1,0,0,0,0,0
0,0,3,2,1,0,3,2,1,1,1,3,5,5,5,5,4,4,3,3,2,1,1,2,1,0,0,0,0,0
0,0,3,2,1,0,3,2,1,0,0,2,4,4,4,4,4,3,3,2,2,1,0,2,1,0,0,0,0,0
0,4,3,2,1,0,3,2,1,0,0,1,3,3,3,4,3,3,2,2,1,1,0,2,1,0,0,0,0,0
0,4,3,2,1,0,3,2,1,0,0,0,2,2,2,3,3,2,2,1,1,0,0,2,1,0,0,0,0,0
0,4,3,2,1,0,3,2,1,0,0,0,1,1,1,2,2,2,1,1,0,0,0,2,1,0,0,0,0,0
3,3,3,2,1,0,3,2,1,0,0,0,0,0,0,1,1,1,1,0,0,0,0,3,2,1,0,0,0,0
2,2,2,2,1,0,2,2,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2,2,1,0,0,0,0
1,1,1,1,1,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0

如果您想使用暴力方法来解决这个问题，您需要尝试以每个单元格为角落的正方形的所有大小（包括1x1）进行标记，将该正方形标记为零，调整左侧/上方7个单元格的值，并在新网格上进行递归。如果您按顺序从上到下，从左到右迭代单元格，则只需从当前行复制网格到底部行，并且只需调整左侧7个单元格的值。我用JS代码测试了此功能，对于网格的前2或3行速度很快（结果为24和44），需要8秒才能完成前4行（结果为70），而需要30分钟才能完成5行（结果为86）。我不会尝试6行。

但是，正如您从此网格中所看到的，可能性的数量非常之大，暴力破解永远不会是一个选项。另一方面，尝试首先添加大正方形，然后使用较小的正方形填充剩余空间，永远无法保证最佳结果，我担心这样的策略太容易被击败。

7,6,5,4,3,2,1,0,0,0,0,0,0,7,6,5,4,3,2,1
6,6,5,4,3,2,1,0,0,0,0,0,0,6,6,5,4,3,2,1
5,5,5,4,3,2,1,0,0,0,0,0,0,5,5,5,4,3,2,1
4,4,4,4,3,2,1,0,0,0,0,0,0,4,4,4,4,3,2,1
3,3,3,3,3,2,1,0,0,0,0,0,0,3,3,3,3,3,2,1
2,2,2,2,2,2,1,0,0,0,0,0,0,2,2,2,2,2,2,1
1,1,1,1,1,1,8,7,6,5,4,3,2,1,1,1,1,1,1,1
0,0,0,0,0,0,7,7,6,5,4,3,2,1,0,0,0,0,0,0
0,0,0,0,0,0,6,6,6,5,4,3,2,1,0,0,0,0,0,0
0,0,0,0,0,0,5,5,5,5,4,3,2,1,0,0,0,0,0,0
0,0,0,0,0,0,4,4,4,4,4,3,2,1,0,0,0,0,0,0
0,0,0,0,0,0,3,3,3,3,3,3,2,1,0,0,0,0,0,0
0,0,0,0,0,0,2,2,2,2,2,2,2,1,0,0,0,0,0,0
7,6,5,4,3,2,1,1,1,1,1,1,1,7,6,5,4,3,2,1
6,6,5,4,3,2,1,0,0,0,0,0,0,6,6,5,4,3,2,1
5,5,5,4,3,2,1,0,0,0,0,0,0,5,5,5,4,3,2,1
4,4,4,4,3,2,1,0,0,0,0,0,0,4,4,4,4,3,2,1
3,3,3,3,3,2,1,0,0,0,0,0,0,3,3,3,3,3,2,1
2,2,2,2,2,2,1,0,0,0,0,0,0,2,2,2,2,2,2,1
1,1,1,1,1,1,1,0,0,0,0,0,0,1,1,1,1,1,1,1

在上面的例子中，将一个8x8的正方形放在中心和四个6x6的正方形放在角落里比将一个6x6的正方形放在中心和四个7x7的正方形放在角落里得到更低的分数；因此，基于使用可能的最大正方形的贪婪方法不会给出最优结果。

这是我通过隔离由最大宽度为3的走廊连接的区域，并在较小的网格上运行暴力算法所达到的程度。当边界没有橙色区域时，添加另外2个单元格不会增加孤立区域的得分，因此这些单元格可以无条件地被主区域使用。

- m69 ''snarky and unwelcoming''

用这些数字描述第一个固定规则的好方法！我有类似的想法，但是我想到了7个布尔表，而不是组合成最大值 - 本质上与比较[yournumber] >= [number looked at]相同。我认为可以_几乎_肯定红色选择是好的...嗯 :-）。其中大多数都是确定的。_显然_拥有更多的7x7是更好的 - _除非_排除了太多更小的正方形。这意味着每个循环深度都需要重新执行步骤1并重新启动。这一点我们知道。但是从7到6，或者到3、2.5、7，呵..我会回来的。 - Stormwind

@Stormwind 我仔细考虑了隔离区和中间区之间的边界。例如，在数字108旁边，我使用了2个单元格，这些单元格也可以用于中间部分；但是，它们只能作为2x2的一部分使用，并且将其从隔离区中取走会使其得分减少4分；因此，使用这2个单元格来进行中间部分没有任何好处。 - m69 ''snarky and unwelcoming''

@Stormwind 再次检查边界后，我修正了一个错误：左上角区域的值为76，无论是否与中间区域重叠。 - m69 ''snarky and unwelcoming''

非常有趣。您在右上角的得分比我们目前发现的要高。您能发布详细的解决方案吗？ - Roxor9999

@Roxor9999 我将右上角分成三个部分并将它们添加在一起；我正在检查以确保没有错误... - m69 ''snarky and unwelcoming''

@Roxor9999 我也无法重现右上角的分数；我的代码肯定有 bug，但我还没有找到它。不过我猜你现在已经有了解决方法，因为 Sascha 给出了答案。 - m69 ''snarky and unwelcoming''

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- sascha · Accepted Answer

这是一个使用混合整数规划的通用原型，可以最优地解决您的实例（我得到了您自己推导出的1112的值），也可能解决其他实例。

一般来说，您的问题是np-complete的，这使得它很难（有些实例会有麻烦）。

虽然我怀疑基于SAT-solver和CP-solver的方法可能更强大（因为组合性质；我甚至惊讶于MIP在这里起作用），但MIP方法也具有一些优点：

MIP-solvers是完备的（与SAT和CP一样；但许多基于随机的启发式算法不是）：
如果需要，有许多商业级别的求解器可用
公式相当简单（特别是与SAT相比；SAT公式将需要高级的最多k个中的n个-公式（对于评分公式），这些公式呈二次增长（朴素方法呈指数增长）！它们确实存在，但并不简单）
优化目标非常自然（SAT和CP需要迭代细化=使用某个下限解决；增加下限并重新解决）
MIP-solvers也可以非常强大地获得最优解的近似值，并提供一些证明边界（例如，最优解低于x）

以下代码是使用通用科学工具实现的python代码（所有这些都是开源的）。它允许设置平铺范围（例如添加9x9平铺）和不同的成本函数。注释应该足以理解这些想法。它将使用一些（可能是最好的）开源MIP求解器，但也可以使用商业版（注释掉的行显示用法）。

import numpy as np
import itertools
from collections import defaultdict
import matplotlib.pyplot as plt     # visualization only
import seaborn as sns               # ""
from pulp import *                  # MIP-modelling & solver

""" INSTANCE """
instance = np.asarray([[1,1,0,0,0,1,0,0,0,0,0,0,1,1,1,1,1,1,0,0,1,1,1,1,1,0,0,1,1,1],
 [1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,1,1,0,0,0,1,1],
 [1,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,1],
 [0,0,0,1,1,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0],
 [0,0,0,0,1,1,0,0,0,0,1,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0],
 [0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,1,1,1],
 [0,0,0,0,0,0,0,0,1,1,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,1,1,1,1],
 [1,0,0,0,0,0,0,1,1,1,1,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,1],
 [1,1,0,0,0,0,0,1,1,1,1,0,0,0,1,1,1,1,1,1,1,1,0,0,1,0,0,0,0,1],
 [1,1,1,0,0,0,0,1,1,1,1,1,0,0,1,1,1,1,1,1,1,0,0,0,1,1,1,0,0,0],
 [0,1,1,1,0,0,0,1,1,1,1,1,0,0,0,0,1,1,1,0,0,0,0,1,1,1,1,0,0,0],
 [0,0,1,1,1,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0],
 [0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0],
 [0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1],
 [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1],
 [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,1],
 [0,0,0,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1],
 [0,0,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0],
 [0,1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0],
 [1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0],
 [1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0],
 [1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0],
 [1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0],
 [1,1,1,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0],
 [0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0],
 [0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1],
 [0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1],
 [0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1],
 [0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1],
 [0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1],
 [0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1],
 [0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1],
 [0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1],
 [0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1],
 [1,1,1,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1],
 [1,1,1,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1],
 [1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1],
 [1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1],
 [1,1,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1],
 [1,1,0,0,0,1,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,1,1,1,1],
 [1,0,0,0,0,1,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,1,1,1,1],
 [1,0,0,0,0,1,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,1,1,0,0,1,1,1,1,1],
 [1,0,0,0,0,1,0,0,0,1,1,1,0,0,0,0,0,0,0,0,1,1,1,0,0,1,1,1,1,1],
 [0,0,0,0,0,1,0,0,0,1,1,1,1,1,1,0,0,0,0,1,1,1,1,0,0,0,1,1,1,1],
 [0,0,0,0,0,1,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1],
 [0,0,0,0,0,1,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]], dtype=bool)

def plot_compare(instance, solution, subgrids):
    f, (ax1, ax2) = plt.subplots(2, sharex=True, sharey=True)
    sns.heatmap(instance, ax=ax1, cbar=False, annot=True)
    sns.heatmap(solution, ax=ax2, cbar=False, annot=True)
    plt.show()

""" PARAMETERS """
SUBGRIDS = 8  # 1x1 - 8x8
SUGBRID_SCORES = {1:0, 2:4, 3:10, 4:20, 5:35, 6:60, 7:84, 8:120}
N, M = instance.shape  # free / to-fill = zeros!

""" HELPER FUNCTIONS """
def get_square_covered_indices(instance, pos_x, pos_y, sg):
    """ Calculate all covered tiles when given a top-left position & size
            -> returns the base-index too! """
    N, M = instance.shape
    neighbor_indices = []
    valid = True
    for sX in range(sg):
        for sY in range(sg):
            if pos_x + sX < N:
                if pos_y + sY < M:
                    if instance[pos_x + sX, pos_y + sY] == 0:
                        neighbor_indices.append((pos_x + sX, pos_y + sY))
                    else:
                        valid = False
                        break
                else:
                    valid = False
                    break
            else:
                valid = False
                break
    return valid, neighbor_indices

def preprocessing(instance, SUBGRIDS):
    """ Calculate all valid placement / tile-selection combinations """
    placements = {}
    index2placement = {}
    placement2index = {}
    placement2type = {}
    type2placement = defaultdict(list)
    cover2index = defaultdict(list)  # cell covered by placement-index

    index_gen = itertools.count()
    for sg in range(1, SUBGRIDS+1):  # sg = subgrid size
        for pos_x in range(N):
            for pos_y in range(M):
                if instance[pos_x, pos_y] == 0:  # free
                    feasible, covering = get_square_covered_indices(instance, pos_x, pos_y, sg)
                    if feasible:
                        new_index = next(index_gen)
                        placements[(sg, pos_x, pos_y)] = covering
                        index2placement[new_index] = (sg, pos_x, pos_y)
                        placement2index[(sg, pos_x, pos_y)] = new_index
                        placement2type[new_index] = sg
                        type2placement[sg].append(new_index)
                        cover2index[(pos_x, pos_y)].append(new_index)

    return placements, index2placement, placement2index, placement2type, type2placement, cover2index

def calculate_collisions(placements, index2placement):
    """ Calculate collisions between tile-placements (position + tile-selection)
        -> only upper triangle is used: a < b! """
    n_p = len(placements)
    coll_mat = np.zeros((n_p, n_p), dtype=bool)  # only upper triangle is used

    for pA in range(n_p):
        for pB in range(n_p):
            if pA < pB:
                covered_A = placements[index2placement[pA]]
                covered_B = placements[index2placement[pB]]
                if len(set(covered_A).intersection(set(covered_B))) > 0:
                    coll_mat[pA, pB] = True

    return coll_mat

""" PREPROCESSING """
placements, index2placement, placement2index, placement2type, type2placement, cover2index = preprocessing(instance, SUBGRIDS)
N_P = len(placements)
coll_mat = calculate_collisions(placements, index2placement)

""" MIP-MODEL """
prob = LpProblem("GridFill", LpMaximize)

# Variables
X = np.empty(N_P, dtype=object)
for x in range(N_P):
    X[x] = LpVariable('x'+str(x), 0, 1, cat='Binary')

# Objective
placement_scores = [SUGBRID_SCORES[index2placement[p][0]] for p in range(N_P)]
prob += lpDot(placement_scores, X), "Score"

# Constraints
# C1: Forbid collisions of placements
for a in range(N_P):
    for b in range(N_P):
        if a < b:  # symmetry-reduction
            if coll_mat[a, b]:
                prob += X[a] + X[b] <= 1  # not both!

""" SOLVE """
print('solve')
#prob.solve(GUROBI())  # much faster commercial solver; if available
prob.solve(PULP_CBC_CMD(msg=1, presolve=True, cuts=True))
print("Status:", LpStatus[prob.status])

""" INTERPRET AND COMPLETE SOLUTION """
solution = np.zeros((N, M), dtype=int)
for x in range(N_P):
    if X[x].value() > 0.99:
        sg, pos_x, pos_y = index2placement[x]
        _, positions = get_square_covered_indices(instance, pos_x, pos_y, sg)
        for pos in positions:
            solution[pos[0], pos[1]] = sg

fill_with_ones = np.logical_and((solution == 0), (instance == 0))
solution[fill_with_ones] = 1

""" VISUALIZE """
plot_compare(instance, solution, SUBGRIDS)

假设 / 算法特点

没有限制需要覆盖每个空闲单元格
- 当不存在负分数时，这种方法有效
- 如果得分为正，则会放置一个得分
- 零分数（如您的示例）可能会保留一些单元格为空闲状态，但这些单元格在优化后被证明是1（添加后）

性能

这是开源和商业求解器之间的差异的一个很好的例子。尝试了两个求解器：cbc 和 Gurobi。

cbc 示例输出（仅部分最终结果）

Result - Optimal solution found

Objective value:                1112.00000000
Enumerated nodes:               0
Total iterations:               307854
Time (CPU seconds):             2621.19
Time (Wallclock seconds):       2627.82

Option for printingOptions changed from normal to all
Total time (CPU seconds):       2621.57   (Wallclock seconds):       2628.24

需要时间：约45分钟

Gurobi示例输出

Explored 0 nodes (7004 simplex iterations) in 5.30 seconds
Thread count was 4 (of 4 available processors)

Optimal solution found (tolerance 1.00e-04)
Best objective 1.112000000000e+03, best bound 1.112000000000e+03, gap 0.0%

需要：6 秒钟

关于求解器性能的一般说明

Gurobi应该具有更多的功能来识别问题的本质并在内部使用适当的超参数
我认为也使用了一些基于SAT的方法（因为其中一位核心开发人员主要撰写了他的论文，介绍了这些非常不同的算法技术的组合）
使用了更好的启发式方法，可以快速提供非最优解（这将有助于之后的步骤）

优化填充网格图形的正方形

假设 / 算法特点

性能

cbc 示例输出（仅部分最终结果）

Gurobi示例输出

关于求解器性能的一般说明

示例输出：得分为1112 的最优解（单击放大）