SDE的参数估计是一个研究级领域,因此相对比较复杂。有关该主题的整本书存在于世上。如需更多详细信息,请随意查看那些书籍。
但这里有一个简单的方法来解决这个问题。首先,注意到对数GBM是一个仿射变换的维纳过程(即线性Ito漂移扩散过程)。所以
d ln(S_t) = (mu - sigma^2 / 2) dt + sigma dB_t
因此我们可以估计对数过程的参数并将其转换为适合原始过程的参数。例如,可以查看[1]、[2]、[3]和[4]等链接。
以下是一段脚本,它以两种简单的方式对漂移进行了估计(只是想看到它们之间的差异),并为扩散估计了一种方法(抱歉只有一种方法)。对数过程的漂移通过(X_T - X_0) / T 和增量最大似然估计法进行估计(请参见代码)。扩散参数以其定义的微小方差的形式被(有偏地)估计。
import numpy as np
np.random.seed(9713)
mu = 1.5
sigma = 0.9
x0 = 1.0
n = 1000
dt = 0.05
T = dt*n
ts = np.linspace(dt, T, n)
def gbm(mu, sigma, x0, n, dt):
step = np.exp( (mu - sigma**2 / 2) * dt ) * np.exp( sigma * np.random.normal(0, np.sqrt(dt), (1, n)))
return x0 * step.cumprod()
def simple_estimate_mu(series):
return (series[-1] - x0) / T
def incremental_estimate_mu(series):
total = (1.0 / dt) * (ts**2).sum()
return (1.0 / total) * (1.0 / dt) * ( ts * series ).sum()
def estimate_sigma(series):
return np.sqrt( ( np.diff(series)**2 ).sum() / (n * dt) )
all_estimates0 = lambda s: (simple_estimate_mu(s), incremental_estimate_mu(s), estimate_sigma(s))
def gbm_drift(log_mu, log_sigma):
return log_mu + 0.5 * log_sigma**2
def all_estimates(es):
lmu1, lmu2, sigma = all_estimates0(es)
return gbm_drift(lmu1, sigma), gbm_drift(lmu2, sigma), sigma
print('Real Mu:', mu)
print('Real Sigma:', sigma)
series = gbm(mu, sigma, x0, n, dt)
log_series = np.log(series)
print('Using 1 series: mu1 = %.2f, mu2 = %.2f, sigma = %.2f' % all_estimates(log_series) )
K = 10000
s = [ np.log(gbm(mu, sigma, x0, n, dt)) for i in range(K) ]
e = np.array( [ all_estimates(si) for si in s ] )
avgs = np.mean(e, axis=0)
print('Using %d series: mu1 = %.2f, mu2 = %.2f, sigma = %.2f' % (K, avgs[0], avgs[1], avgs[2]) )
输出结果:
Real Mu: 1.5
Real Sigma: 0.9
Using 1 series: mu1 = 1.56, mu2 = 1.54, sigma = 0.96
Using 10000 series: mu1 = 1.51, mu2 = 1.53, sigma = 0.93
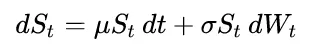
scipy.optimize.curve_fit。 - Gergessymfit包,使得在 Python 中处理这样的拟合过程变得更加容易。 - tBuLi