我为计算任务解决了以下问题,但是我得到了非常糟糕的成绩(67%),我想了解如何正确地完成这些问题,特别是Q1.b和Q3。请尽可能详细,我真的很想理解我的错误。
生成数据(正弦函数)。使用FFT进行分析: a)三个具有恒定但不同频率的波的叠加 b)频率随时间变化的波 用适当的轴绘制图形、采样频率、振幅和功率谱。
使用Exercise 1a)中的三个波,但将它们更改为具有相同的频率、相位和振幅。随着随机高斯分布噪声逐渐增加,对每个波进行污染。 1)对三个噪声受污染的波的叠加执行FFT。分析并绘制输出。 2)使用高斯函数过滤信号,绘制“清洁”波形,并分析结果。得到的波形是否100%干净?请解释。
生成数据(正弦函数)。使用FFT进行分析: a)三个具有恒定但不同频率的波的叠加 b)频率随时间变化的波 用适当的轴绘制图形、采样频率、振幅和功率谱。
使用Exercise 1a)中的三个波,但将它们更改为具有相同的频率、相位和振幅。随着随机高斯分布噪声逐渐增加,对每个波进行污染。 1)对三个噪声受污染的波的叠加执行FFT。分析并绘制输出。 2)使用高斯函数过滤信号,绘制“清洁”波形,并分析结果。得到的波形是否100%干净?请解释。
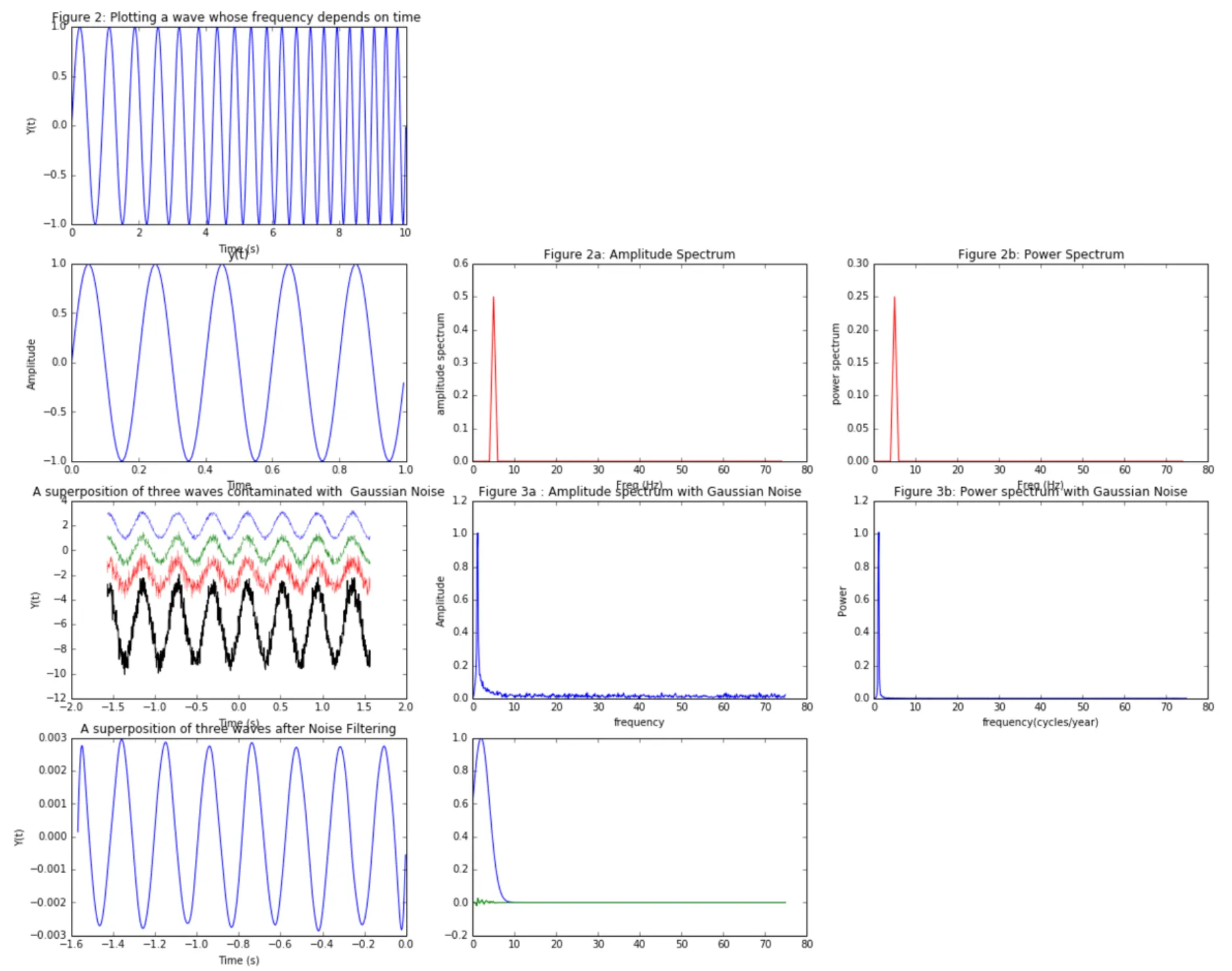
#1(b)
tmin = -2*pi
tmax - 2*pi
delta = 0.01
t = arange(tmin, tmax, delta)
y = sin(2.5*t*t)
plot(t, y, '-')
title('Figure 2: Plotting a wave whose frequency depends on time ')
xlabel('Time (s)')
ylabel('Y(t)')
show()
#b.2
Fs = 150.0; # sampling rate
Ts = 1.0/Fs; # sampling interval
t = np.arange(0,1,Ts) # time vector
ff = 5; # frequency of the signal
y = np.sin(2*np.pi*ff*t)
n = len(y) # length of the signal
k = np.arange(n)
T = n/Fs
frq = k/T # two sides frequency range
frq = frq[range(n/2)] # one side frequency range
Y = np.fft.fft(y)/n # fft computing and normalization
Y = Y[range(n/2)]
#Time vs. Amplitude
plot(t,y)
title('Figure 2: Time vs. Amplitude')
xlabel('Time')
ylabel('Amplitude')
plt.show()
#Amplitude Spectrum
plot(frq,abs(Y),'r')
title('Figure 2a: Amplitude Spectrum')
xlabel('Freq (Hz)')
ylabel('amplitude spectrum')
plt.show()
#Power Spectrum
plot(frq,abs(Y)**2,'r')
title('Figure 2b: Power Spectrum')
xlabel('Freq (Hz)')
ylabel('power spectrum')
plt.show()
#Exercise 3:
#part 1
t = np.linspace(-0.5*pi,0.5*pi,1000)
#contaminating our waves with successively increasing white noise
y_1 = sin(15*t) + np.random.normal(0,0.2*pi,1000)
y_2 = sin(15*t) + np.random.normal(0,0.3*pi,1000)
y_3 = sin(15*t) + np.random.normal(0,0.4*pi,1000)
y = y_1 + y_2 + y_3 # superposition of three contaminated waves
#Plotting the figure
plot(t,y,'-')
title('A superposition of three waves contaminated with Gaussian Noise')
xlabel('Time (s)')
ylabel('Y(t)')
show()
delta = pi/1000.0
n = len(y) ## calculate frequency in Hz
freq = fftfreq(n, delta) # Computing the FFT
Freq = fftfreq(len(y), delta) #Using Fast Fourier Transformation to #calculate frequencies
N = len(Freq)
fr = Freq[1:len(Freq)/2.0]
A = fft(y)
XF = A[1:len(A)/2.0]/float(len(A[1:len(A)/2.0]))
# Amplitude spectrum for contaminated waves
plt.plot(fr, abs(XF))
title('Figure 3a : Amplitude spectrum with Gaussian Noise')
xlabel('frequency')
ylabel('Amplitude')
show()
# Power spectrum for contaminated waves
plt.plot(fr,abs(XF)**2)
title('Figure 3b: Power spectrum with Gaussian Noise')
xlabel('frequency(cycles/year)')
ylabel('Power')
show()
# part 2
F_v = exp(-(abs(freq)-2)**2/2*0.5**2)
spectrum = A*F_v #Applying the Gaussian Filter to clean our waves
new_y = ifft(spectrum) #Computing the inverse FFT
plot(t,new_y,'-')
title('A superposition of three waves after Noise Filtering')
xlabel('Time (s)')
ylabel('Y(t)')
show()