K-means算法中的聚类中心约束问题

Question

我正在为我的数据科学入门课程做一个数据科学项目，我们决定解决与加利福尼亚州淡化海水厂有关的问题：“在哪里放置k个工厂以最小化邮编之间的距离？”

到目前为止，我们已经获得了这些数据：邮编、城市、县、人口、纬度、经度、用水量。

问题是，我找不到任何资源来强制限制质心留在海岸线上。 我们目前考虑的解决方案是： - 使用普通的kmeans算法，但在簇团已经稳定之后将质心移动到海岸线上（不好）。 - 使用带权重的普通kmeans算法，使沿海的邮编具有无限权重（我被告知这不是一个很好的方案）。

你们认为呢？

- Dee Ess

---

我是IANA的数据科学家，但你能将海岸线离散化，然后选择那些具有最小簇内平方和的吗？重新定义更新步骤会更难。我现在要深入思考一下这个问题。 - Nathaniel Rivera Saul

我认为我的初始想法不会很好地扩展。相反，您可以重新定义更新步骤，将新的平均值投影回海岸线。这应该很简单。首先计算新的平均值，然后找到最接近该新平均值的海岸点。算法将继续尝试将平均值从海岸线上拉开，而您必须将它们推回去。我预计最终增量将垂直于海岸线，但这只是猜测。 - Nathaniel Rivera Saul

Answer 1

我会通过设置可能的中心点来处理这个问题，例如你的海岸线。
我认为这与Nathaniel Saul的第一个评论很接近。
这样，在每次迭代中，不是选择平均值，而是选择可能集合中靠近聚类的点。

我已将条件简化为仅包含2个数据列（经度和纬度），但您应该能够推广这个概念。为了演示简单，我基于此处的代码。

在这个例子中，紫色的点是沿海的地方。如果我理解正确，最佳的海岸线位置应该看起来像这样：

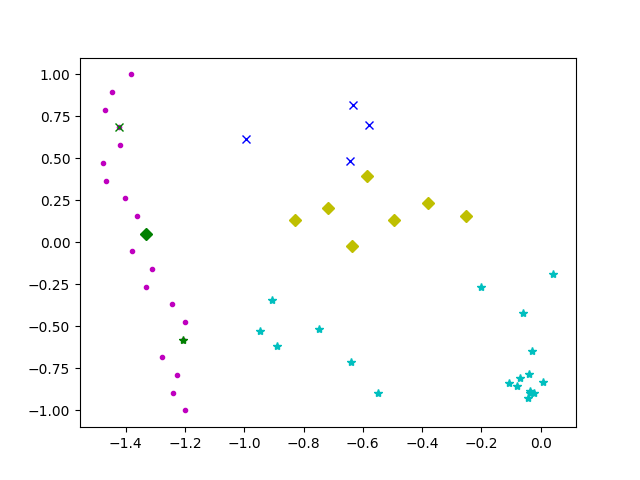
请看下方代码：

#! /usr/bin/python3.6

# Code based on:
# https://datasciencelab.wordpress.com/2013/12/12/clustering-with-k-means-in-python/

import matplotlib.pyplot as plt
import numpy as np
import random

##### Simulation START #####
# Generate possible points.
def possible_points(n=20):
    y=list(np.linspace( -1, 1, n ))
    x=[-1.2]
    X=[]
    for i in list(range(1,n)):
        x.append(x[i-1]+random.uniform(-2/n,2/n) )
    for a,b in zip(x,y):
        X.append(np.array([a,b]))
    X = np.array(X)
    return X

# Generate sample
def init_board_gauss(N, k):
    n = float(N)/k
    X = []
    for i in range(k):
        c = (random.uniform(-1, 1), random.uniform(-1, 1))
        s = random.uniform(0.05,0.5)
        x = []
        while len(x) < n:
            a, b = np.array([np.random.normal(c[0], s), np.random.normal(c[1], s)])
            # Continue drawing points from the distribution in the range [-1,1]
            if abs(a) < 1 and abs(b) < 1:
                x.append([a,b])
        X.extend(x)
    X = np.array(X)[:N]
    return X
##### Simulation END #####    

# Identify points for each center.
def cluster_points(X, mu):
    clusters  = {}
    for x in X:
        bestmukey = min([(i[0], np.linalg.norm(x-mu[i[0]])) \
                    for i in enumerate(mu)], key=lambda t:t[1])[0]
        try:
            clusters[bestmukey].append(x)
        except KeyError:
            clusters[bestmukey] = [x]
    return clusters

# Get closest possible point for each cluster.
def closest_point(cluster,possiblePoints):
    closestPoints=[]
    # Check average distance for each point.
    for possible in possiblePoints:
        distances=[]
        for point in cluster:
            distances.append(np.linalg.norm(possible-point))
            closestPoints.append(np.sum(distances)) # minimize total distance
            # closestPoints.append(np.mean(distances))
    return possiblePoints[closestPoints.index(min(closestPoints))]

# Calculate new centers.
# Here the 'coast constraint' goes.
def reevaluate_centers(clusters,possiblePoints):
    newmu = []
    keys = sorted(clusters.keys())
    for k in keys:
        newmu.append(closest_point(clusters[k],possiblePoints))
    return newmu

# Check whether centers converged.
def has_converged(mu, oldmu):
    return (set([tuple(a) for a in mu]) == set([tuple(a) for a in oldmu]))

# Meta function that runs the steps of the process in sequence.
def find_centers(X, K, possiblePoints):
    # Initialize to K random centers
    oldmu = random.sample(list(possiblePoints), K)
    mu = random.sample(list(possiblePoints), K)
    while not has_converged(mu, oldmu):
        oldmu = mu
        # Assign all points in X to clusters
        clusters = cluster_points(X, mu)
        # Re-evaluate centers
        mu = reevaluate_centers(clusters,possiblePoints)
    return(mu, clusters)


K=3
X = init_board_gauss(30,K)
possiblePoints=possible_points()
results=find_centers(X,K,possiblePoints)

# Show results

# Show constraints and clusters
# List point types
pointtypes1=["gx","gD","g*"]

plt.plot(
    np.matrix(possiblePoints).transpose()[0],np.matrix(possiblePoints).transpose()[1],'m.'
    )

for i in list(range(0,len(results[0]))) :
    plt.plot(
        np.matrix(results[0][i]).transpose()[0], np.matrix(results[0][i]).transpose()[1],pointtypes1[i]
        )

pointtypes=["bx","yD","c*"]
# Show all cluster points
for i in list(range(0,len(results[1]))) :
    plt.plot(
        np.matrix(results[1][i]).transpose()[0],np.matrix(results[1][i]).transpose()[1],pointtypes[i]
        )
plt.show()

编辑以最小化总距离。

- AChervony

Answer 2

K-means不是最小化距离。

它最小化平方误差，这是非常不同的。 两者的区别大致相当于一维数据中的中位数和平均数。误差可能非常大。

以下是一个反例，假设我们有以下坐标：

-1 0
+1 0
 0 -1
 0 101

通过k-means选择的中心点是0,25。最优位置是0,0。 k-means的距离总和> 152，最优位置的距离为104。因此，在这里，质心比最优解差了近50％！但是，质心（=多元均值）是k-means使用的！

k-means不会最小化欧几里得距离！

这是"k-means对异常值敏感"的一种变体。

如果您尝试将其限制在仅沿海放置“中心”，它并不会变得更好...

此外，您可能至少应该使用Haversine距离，因为在加利福尼亚州，1度北纬！= 1度东经，因为它不在赤道上。

此外，您可能不应该假设每个位置都需要自己的管道，而是它们将像树一样连接起来。这大大降低了成本。

我强烈建议将其视为通用优化问题，而不是k-means。 K-means也是一种优化，但它可能会为您的问题优化错误的函数...

- Has QUIT--Anony-Mousse