logo标签列表

在C/C++中实现导数

c++calgorithmmathnumerical-methods
26
展示一下你目前完成的工作。 - Lazarus
11
你希望我被解雇吗？ :) - vehomzzz
5
牛顿迭代法的精度并不仅取决于导数的精度，即使是较粗略的逼近也可以使用（在极端情况下，你会得到割线法），但需要更多迭代才能达到相同的精度，因此速度会稍微慢一些。 - fortran
8个回答
65
我同意@erikkallen的观点，(f(x + h) - f(x - h)) / (2 * h) 是数值近似导数的常用方法。然而，选择正确的步长h有点微妙。
在(f(x + h) - f(x - h)) / (2 * h)中，近似误差随着h的减小而减小，这意味着你应该选择尽可能小的h。但是，随着h的减小，浮点数减法引起的误差增加，因为分子需要减去几乎相等的数。如果h太小，减法运算中会损失很多精度。因此，在实践中，你必须选择一个既不太小又能最小化“近似误差”和“数值误差”组合的h值。
作为一个经验法则，你可以尝试使用h = SQRT(DBL_EPSILON)，其中DBL_EPSILON是机器精度下最小的双精度数e，满足1 + e != 1。 DBL_EPSILON约为10^-15，所以你可以使用h = 10^-7或10^-8。
要了解更多细节，请参阅有关选择微分方程步长的注释。
此外，如果你想要非常精确的结果，你可以使用Eigen库。首先尝试以下未更改的代码，然后取消注释带有Eigen包含的第一行。
// #include "Eigen/Dense" // uncomment this, and check the result

#include <functional>
#include <iostream>
#include <limits>
#include <cmath>

typedef std::function<double(double)> RealFunc;
typedef std::function<double(std::function<double(double)>, double)> RealFuncDerivative;

double FibonacciFunc(double x) {
    return pow(x, 3) + 2.0 * pow(x, 2) + 10.0 * x - 20.0;
}

double derivative(RealFunc f, double x) {
    double h = sqrt(std::numeric_limits<double>::epsilon());
    return (f(x + h) - f(x - h)) / (2.0 * h);
}

double NewtonsMethod(RealFunc f, RealFuncDerivative d, double x0, double precision) {
    double x = x0;
    for (size_t i = 0;; i++) {
        x = x - (f(x) / d(f, x));

        if (abs(f(x)) < precision) {
            return x;
        }
    }
}

int main() {
    RealFunc f{FibonacciFunc};
    RealFuncDerivative d{derivative};

    std::cout << NewtonsMethod(f, d, 1.0, 10e-4) << "\n";
}

第一次运行的结果应该是1.41176，而使用Eigen库的结果应该是1.36881（都是使用2次迭代计算得出的）。这第二个结果与使用5位小数的解析基准结果完全相等。
你观察到的结果差异是由于Eigen影响了你的代码中的浮点精度设置和舍入模式，以优化其自身操作的数值稳定性和性能。这可以导致更好的结果，特别是当你使用敏感的数值算法，如牛顿-拉夫逊方法时。
请注意，即使使用较大的h（例如h=10而不是h=SQRT(DBL_EPSILON)），使用Eigen的算法仍然能够相当好地收敛，尽管速度较慢（在47次迭代下为1.36877）。总而言之，虽然不是必需的，但尽可能使用较小的h仍然是首选。
4
我认为你的经验法则假设你使用一阶规则来近似导数。然而，你提到的中心差分规则是二阶的，相应的经验法则是h = EPSILON^(1/3)，在使用双精度时大约为10^(-5)。 - Jitse Niesen
我认为通过除以(x+h)-(x-h)而不是2h，可以稍微提高准确性。数学上是等价的，但在数值上不一样。 - sellibitze
1
你的意思是 "DBL_EPSILON 是最小的双精度数字 e，使得在机器精度下 1 + e != 1。" 吗？ - yves Baumes
2
选择h取决于导数f'''(x)。 - Alexey Malistov
+1 个好答案。我肯定会忽略 h 的非常小的尺寸，这会放大浮点误差。谢谢，今天我学到了一些东西。 - MAK
作为一个经验法则，取代之前的是“你所知道的f的精度的立方根”乘以f的数量级。你的二阶有限差分在精度（f）^2/3的截断和舍入误差上。 - Alexandre C.
11

牛顿-拉弗森法（Newton_Raphson）假定您可以拥有两个函数 f(x) 及其导数 f'(x)。如果您没有可用的导数函数并且必须从原始函数估计导数，则应使用另一种根查找算法。

维基百科根查找 给出了几个建议，就像任何数值分析文本一样。

10

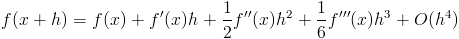
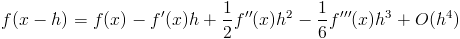
alt text

alt text

1）第一种情况：

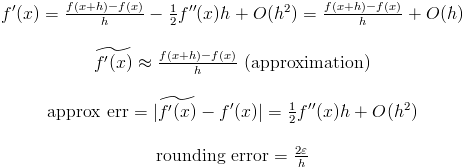
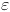alt text

alt text — 相对误差约为双精度 2^{-16} 和单精度 2^{-7}。

我们可以计算总误差：

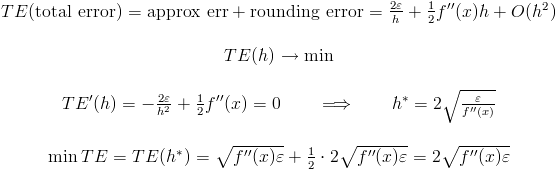
alt text

假设您正在使用双浮点运算。因此，h 的最佳值是 2sqrt(DBL_EPSILON/f''(x))。你不知道 f''(x)。但你必须估计这个值。例如，如果 f''(x) 约为 1，则 h 的最佳值为 2^{-7}，但如果 f''(x) 约为 10^6，则 h 的最佳值为 2^{-10}！

2）第二种情况:

alt text

请注意，第二个近似误差比第一个近似误差更快地趋近于零。但如果 f'''(x) 很大，则第一种选项更可取：

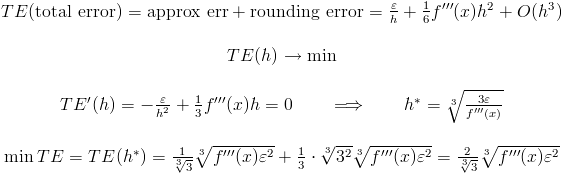
alt text

请注意，在第一种情况下，h 与 e 成正比，而在第二种情况下，h 与 e^{1/3} 成正比。对于双精度浮点运算，e^{1/3} 约为 2^{-5} 或 2^{-6}。（我假设 f'''(x) 约为 1）。

哪种方法更好？ 如果您不知道f''(x)和f'''(x)，或者您无法估计这些值，则未知。据信第二个选项更可取。但是，如果您知道f'''(x)非常大，请使用第一个选项。

h的最佳值是多少？ 假设f''(x)和f'''(x)约为1。并且假设我们使用双精度浮点运算。那么在第一种情况下，h约为2^{-8}，在第二种情况下，h约为2^{-5}。如果您知道f''(x)或f'''(x)，请更正这些值。

epsilon应该是2的-53次方，适用于双精度浮点数，而对于单精度浮点数则为2的-24次方（分别约为10的-16次方和10的-7次方）。 - Stephen Canon
Epsilon是相对舍入误差（而非绝对误差）。对于双精度浮点数，它始终约为10^{-16}，对于单精度浮点数，则约为10^{-7}。 - Alexey Malistov
是的，我知道。在你的回答中，你说“epsilon - 相对舍入误差，对于双精度约为2^{-16}，对于浮点数约为2^{-7}”，这是明显错误的。相对（前向）舍入误差也不总是在那个范围内，而是后向误差。当发生抵消时，前向误差可能会大得多，这在这里很可能发生。 - Stephen Canon
ImageShack的图片目前无法显示。 - kibibu
1
评估误差更正确地是 abs(f(x))*eps 的倍数，其中多重性与评估 f(x) 中的浮点运算次数有关。因此，对于中心差分，h~cbrt(abs(f(x)/f'''(x))*eps)。 - Lutz Lehmann
6
fprime(x) = (f(x+dx) - f(x-dx)) / (2*dx)

对于一些小的 DX。

1
Numerical Receipes对此有一些评论 http://books.google.co.uk/books?id=1aAOdzK3FegC&printsec=frontcover&dq=related:ISBN0521437202#v=onepage&q=newton-Raphson&f=false - mmmmmm
5

当你选择h的值时，考虑John Cook的建议是很重要的，但通常不要使用中心差分来近似导数。主要原因是如果你使用前向差分，它会多消耗一个函数计算。

f'(x) = (f(x+h) - f(x))/h

由于您已经需要计算牛顿法中的f（x），所以您将免费获取f（x）的值。当您有一个标量方程时，这并不是什么大问题，但如果x是一个向量，则f'（x）是一个矩阵（雅可比矩阵），并且您需要进行n个额外的函数评估，使用居中差分方法来近似它。

5

你对f(x)了解多少？如果只有f作为一个黑盒子，你唯一能做的就是数值逼近导数。但是精度通常不太好。

如果你可以接触计算f的代码，你可以做得更好。尝试"自动微分"。有一些很好的库可用。通过一点库的魔法，你可以轻松地将函数转换为自动计算导数的东西。对于一个简单的C++例子，请参见此处德国讨论中的源代码。

3

除了John D. Cook上面的回答之外，重要的是不仅要考虑浮点精度，还要考虑函数f(x)的鲁棒性。例如，在金融领域中，f(x)实际上是蒙特卡罗模拟，f(x)的值具有一定的噪声。在这些情况下，使用非常小的步长可能会严重降低导数的准确性。

1
通常，信号噪声对导数质量的影响最大。如果您的 f(x) 中存在噪声，Savtizky-Golay 是一种优秀的平滑算法，经常用于计算良好的导数。简而言之，SG 在本地拟合多项式到您的数据中，然后可以使用该多项式来计算导数。
保罗
网页内容由stack overflow 提供, 点击上面的
可以查看英文原文，
原文链接