我正在寻找一种在不改变贝塞尔曲线形状的情况下插入新控制点的算法。
有没有人知道关于贝塞尔算法(插值,优化,de Casteljau等)的库或参考资料?
我正在寻找一种在不改变贝塞尔曲线形状的情况下插入新控制点的算法。
有没有人知道关于贝塞尔算法(插值,优化,de Casteljau等)的库或参考资料?
这被称为“结点插入问题”。对于Bézier曲线,de Casteljau算法将给出正确的答案。下面是三次Bézier曲线的简单算法。
假设您希望在由P0,P1,P2,P3定义的Bézier曲线的参数空间的分数t处插入一个结点。以下是具体步骤:
P0_1 = (1-t)*P0 + t*P1
P1_2 = (1-t)*P1 + t*P2
P2_3 = (1-t)*P2 + t*P3
P01_12 = (1-t)*P0_1 + t*P1_2
P12_23 = (1-t)*P1_2 + t*P2_3
P0112_1223 = (1-t)*P01_12 + t*P12_23
那么你的第一个贝塞尔曲线将由:P_0,P0_1,P01_12,P0112_1223定义;你的第二个贝塞尔曲线将由:P0112_1223,P12_23,P2_3,P3定义。
几何解释很简单:在贝塞尔多边形的每个线段上按比例划分点,然后连接这些划分点形成一个新的多边形并重复此过程。当只剩下一个点时,该点位于曲线上,前/后一个划分点形成前/后一个贝塞尔多边形。相同的算法也适用于更高阶的贝塞尔曲线。
如果您想在空间中的特定位置插入控制点,则可能会变得更加棘手。个人建议,在此处可使用二分查找来查找接近所需划分点的t值......但如果性能很关键,您可能可以找到更快速的解析解决方案。
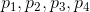 的三次贝塞尔曲线可以写成:
的三次贝塞尔曲线可以写成:
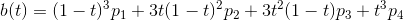 它关于
它关于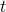 的导数是
的导数是
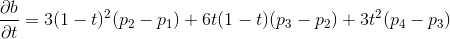 为了将曲线限制在
为了将曲线限制在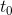 到
到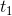 之间,您需要新的控制点
之间,您需要新的控制点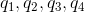 :
:
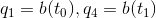
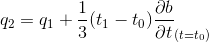
 证明:
证明: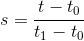
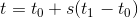 我们得到
我们得到
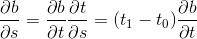 子曲线的第一个和最后一个点是新的第一个和最后一个控制点
子曲线的第一个和最后一个点是新的第一个和最后一个控制点
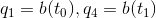
这些点的切线为
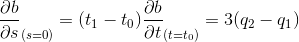
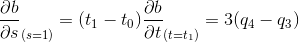
因此
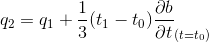

gimpbezierstroke.c 中。有关插入新锚点的参考,请搜索 gimp_bezier_stroke_anchor_insert 。