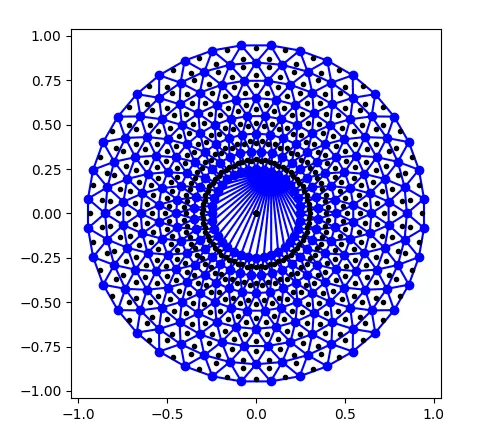
如果我使用matplotlib为一组点生成Delaunay三角剖分,那么获取已生成的三角形的外心的最合适方法是什么?我还没有找到Triangulation库中明显的方法来实现这一点。
3个回答
3
你应该可以使用
matplotlib.delaunay.triangulate.Triangulation来计算它:
Triangulation(x, y) x, y -- 作为浮点数的一维数组的点的坐标
. . .
Attributes: (all should be treated as read-only to maintain consistency) x, y -- the coordinates of the points as 1-D arrays of floats.
circumcenters -- (ntriangles, 2) array of floats giving the (x,y) coordinates of the circumcenters of each triangle (indexed by a triangle_id).
这段内容是从matplotlib的一个示例中改编而来(可能有更简洁的方法,但以下方法应该可行):
import matplotlib.pyplot as plt
import matplotlib.delaunay
import matplotlib.tri as tri
import numpy as np
import math
# Creating a Triangulation without specifying the triangles results in the
# Delaunay triangulation of the points.
# First create the x and y coordinates of the points.
n_angles = 36
n_radii = 8
min_radius = 0.25
radii = np.linspace(min_radius, 0.95, n_radii)
angles = np.linspace(0, 2*math.pi, n_angles, endpoint=False)
angles = np.repeat(angles[...,np.newaxis], n_radii, axis=1)
angles[:,1::2] += math.pi/n_angles
x = (radii*np.cos(angles)).flatten()
y = (radii*np.sin(angles)).flatten()
tt = matplotlib.delaunay.triangulate.Triangulation(x,y)
triang = tri.Triangulation(x, y)
# Plot the triangulation.
plt.figure()
plt.gca().set_aspect('equal')
plt.triplot(triang, 'bo-')
plt.plot(tt.circumcenters[:,0],tt.circumcenters[:,1],'r.')
plt.show()
- JoshAdel
1
很遗憾,Matplotlib的最新版本中已经删除了circumcenters属性。 - TommasoF
2
这里有一个计算它们的函数。它也可以用于其他三角剖分结构,例如
根据@JoshAdel在上面的回答中提供的数据,添加以下代码:
scipy的Delaunay 三角剖分(见下文)。def compute_triangle_circumcenters(xy_pts, tri_arr):
"""
Compute the centers of the circumscribing circle of each triangle in a triangulation.
:param np.array xy_pts : points array of shape (n, 2)
:param np.array tri_arr : triangles array of shape (m, 3), each row is a triple of indices in the xy_pts array
:return: circumcenter points array of shape (m, 2)
"""
tri_pts = xy_pts[tri_arr] # (m, 3, 2) - triangles as points (not indices)
# finding the circumcenter (x, y) of a triangle defined by three points:
# (x-x0)**2 + (y-y0)**2 = (x-x1)**2 + (y-y1)**2
# (x-x0)**2 + (y-y0)**2 = (x-x2)**2 + (y-y2)**2
#
# becomes two linear equations (squares are canceled):
# 2(x1-x0)*x + 2(y1-y0)*y = (x1**2 + y1**2) - (x0**2 + y0**2)
# 2(x2-x0)*x + 2(y2-y0)*y = (x2**2 + y2**2) - (x0**2 + y0**2)
a = 2 * (tri_pts[:, 1, 0] - tri_pts[:, 0, 0])
b = 2 * (tri_pts[:, 1, 1] - tri_pts[:, 0, 1])
c = 2 * (tri_pts[:, 2, 0] - tri_pts[:, 0, 0])
d = 2 * (tri_pts[:, 2, 1] - tri_pts[:, 0, 1])
v1 = (tri_pts[:, 1, 0] ** 2 + tri_pts[:, 1, 1] ** 2) - (tri_pts[:, 0, 0] ** 2 + tri_pts[:, 0, 1] ** 2)
v2 = (tri_pts[:, 2, 0] ** 2 + tri_pts[:, 2, 1] ** 2) - (tri_pts[:, 0, 0] ** 2 + tri_pts[:, 0, 1] ** 2)
# solve 2x2 system (see https://en.wikipedia.org/wiki/Invertible_matrix#Inversion_of_2_%C3%97_2_matrices)
det = (a * d - b * c)
detx = (v1 * d - v2 * b)
dety = (a * v2 - c * v1)
x = detx / det
y = dety / det
return (np.vstack((x, y))).T
根据@JoshAdel在上面的回答中提供的数据,添加以下代码:
cc = compute_triangle_circumcenters(np.vstack([tt.x, tt.y]).T, tt.triangle_nodes)
plt.plot(cc[:, 0], cc[:, 1], ".k")
我得到了下面的图形:
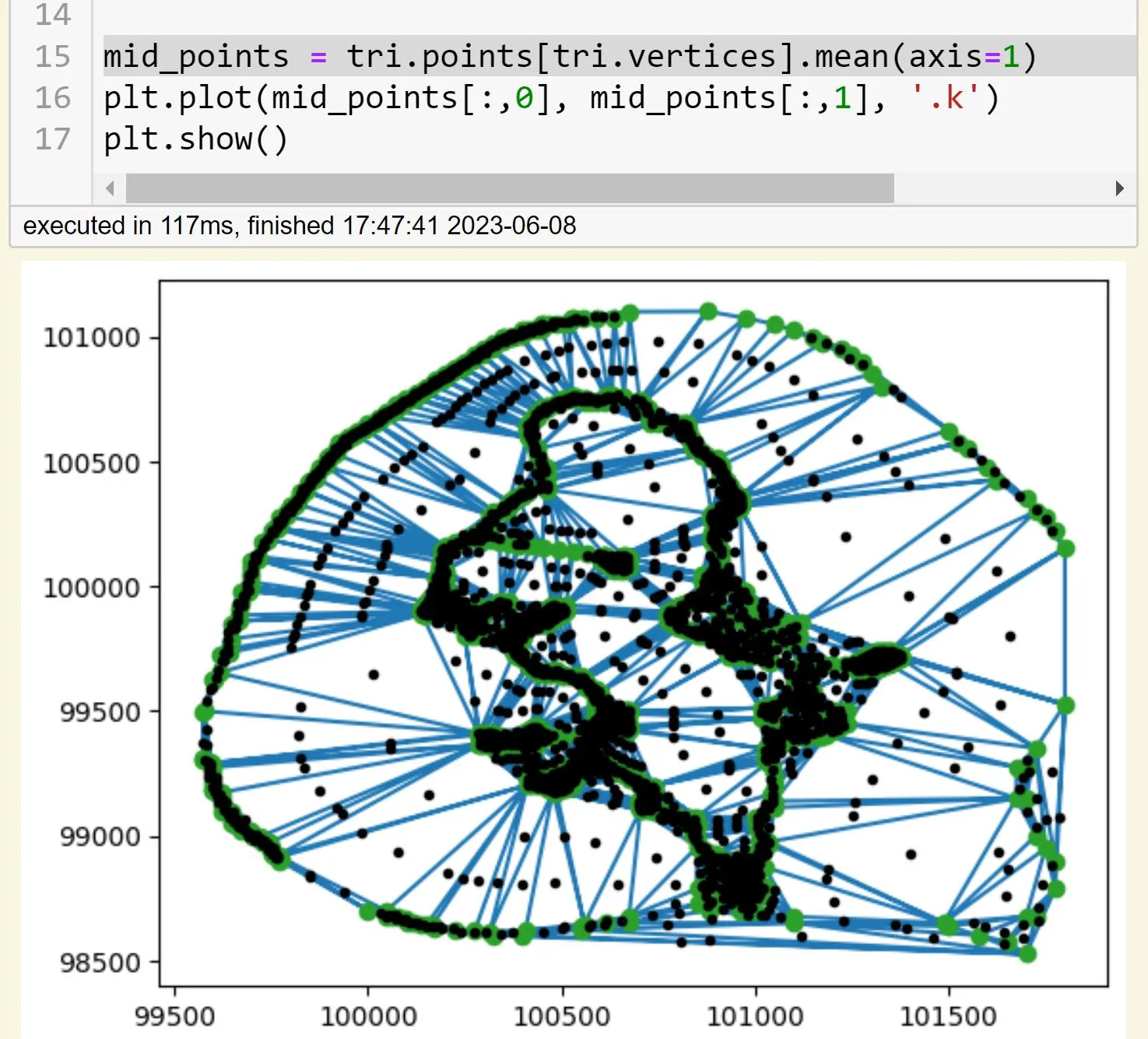
它也可以像这样用于scipy.spatial.Delaunay:
from scipy.spatial import Delaunay
xy_pts = np.vstack([x, y]).T
dt = Delaunay(xy_pts)
cc = compute_triangle_circumcenters(dt.points, dt.simplices)
- Iddo Hanniel
网页内容由stack overflow 提供, 点击上面的可以查看英文原文,
原文链接
原文链接