如何确定一个向量是否在另外两个向量之间？

Question

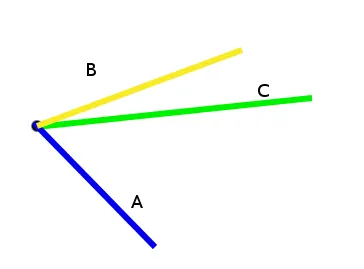
我正在寻找一种快速有效的方法来确定向量B是否位于向量A和向量C之间的小角度内。通常我会使用垂直点积来确定B在每条线的哪一侧，但由于以下原因，这种方法并不简单：

• 不能假设任何向量都已归一化，而归一化它们是我希望避免的额外步骤。
• 我没有清晰的概念来确定最小角度的哪一侧是好的或不好的。
• A和B可能共线或正好相隔180度，在这种情况下我想返回false。
• 虽然我在三维环境中工作，但如果能使事情更简单、更重要的是更快地运行，那么将其简化为二维就很容易了。这个测试将用于需要尽可能快地运行的算法中。

如果有一种简单有效的方法可以确定我的垂直向量应该指向哪个方向，我可以使用两个点积进行测试。

我一直在考虑另一种方法，但迄今为止没有太大成功，即使用矩阵。理论上，从我对矩阵变换的理解中，我应该能够使用A和C作为基向量。然后通过矩阵乘法将B乘以矩阵，我应该能够通过X和Y都为正来测试B位于哪个象限内。如果我能使这种方法起作用，那么它可能是最好的，因为一次矩阵乘法应该比两个点积快，而且我不必担心哪一侧具有最小的角度。

问题在于从我的测试中，我不能简单地将A和C作为基础并正常地进行矩阵乘法，以获得正确的行为。我真的不确定我在做什么方面出了问题。我多次遇到过“向量空间”这个术语，据我所知，它似乎是一个非常类似于矩阵变换的概念，没有对正交基或标准正交基的任何要求。它是否与矩阵相同？如果不是，可能有更好的方法吗？我应该如何使用它？

只是为了更好地解释我所说的：

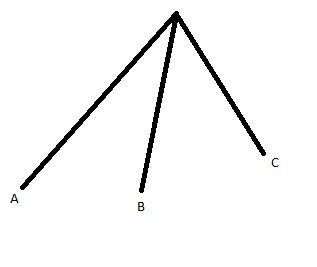
@Aki Suihkonen 我好像无法让它工作。编写了一个我可以运行的模拟案例，看看能否找出问题。

对于这种情况，使用：

Ax 2.9579773 Ay 3.315979

Cx 2.5879822 Cy 5.1630249

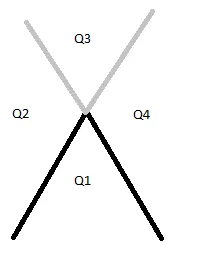
对于B，我围绕向量将空间划分为四个象限进行旋转。

我得到的符号是： - 对于Q1 -- - 对于Q2 +- - 对于Q3 +- - 对于Q4 --

假设我沿着与图像相同的方向在环境中旋转，我相当确定我已经这样做了。

- user1759679

---

你正在使用什么语言/环境进行开发？优化总是与上下文有关。 - Phil H

为什么不尝试使用高斯方法解决向量方程xA+yC=B的问题呢？如果存在解，那么正的x和y都意味着B在A和C之间。 - unixmin

我目前从事C++编程工作，但我对数学优化方面很感兴趣。 - user1759679

如果您想将A，[B]，C旋转，使得B面朝“上”，即y>0，x=0，则标准是sign(A.x)!=sign(C.x)。然而，“中间”意味着仍有一些主观性（例如，如果三个向量是任意的，并且a和c都朝向b的“后方”。（请思考粗体黑线是A和C，向量B指向“q3”）。它是否在中间？公式说是。另一个额外的标准是当A和C被B旋转时，A和C的x符号也必须为正。（并且y符号必须不同） - Aki Suihkonen

Answer 1

我认为Aki的方案接近正确，但有些情况下它并不适用：

从他的解决方案中得到：

return (ay * bx - ax * by) * (ay * cx - ax * cy) < 0;

这相当于检查B和A的叉积与C和A的叉积是否具有相同的符号。

叉积（U x V）的符号告诉您V是否在U的一侧或另一侧（出板面，进板面）。在大多数坐标系统中，如果U需要逆时针旋转（出板面），则符号将为正。

因此，Aki的解决方案检查B是否需要朝一个方向旋转才能到达A，而C则需要朝另一个方向旋转。如果是这种情况，则B不在A和C之内。当您不知道A和C的“顺序”时，此解决方案无法工作，如下所示：

要确切地知道B是否在A和C之内，您需要双向检查。也就是说，从A到B的旋转方向应与从A到C的旋转方向相同，并且从C到B的旋转方向应与从C到A的旋转方向相同。

这可以简化为：

if (AxB * AxC >= 0 && CxB * CxA >= 0)

// then B is definitely inside A and C

- AndyG

---

感谢您提供这个简洁的解决方案。对于其他人来说，AxB 指的是 ay*bx-ax*by（三维叉积的 Z 分量）。如果您想处理边缘情况（A==B 或零向量），则需要进行一些额外的检查。 - Patrick Stalph

一定很难只是打出来，而与此同时，成千上万的人在打字时苦于错别字。谢谢。 - user431806

Answer 2

一种思考这个问题的方法是将所有这些向量A、B、C看作复数。

将A、C乘以B*，其中B*是B的共轭复数，得到的两个向量都将在复平面中被旋转，使参考轴(B*Conj(B))现在成为实轴(或y = 0) -- 而且这个轴不需要计算。在这种情况下，只需检查“y”或虚部的符号是否不同即可。此外，在这种情况下，两个结果向量的长度都被缩放了相同的|B|。

`return sign(Imag(A * Conj(B))) != sign(Imag(C * Conj(B)));`

A = ax + i * ay; B = bx + i * by; C = cx + i * cy;
Conj(B) = bx - i * by; 
A * B = (ax * bx - ay * by) + i * (ax * by + ay * bx);

我认为这个公式可以带来更好的性能，因为只需要使用乘法的虚部。

作为一个完整的解决方案，可转换为：

return (ay * bx - ax * by) * (ay * cx - ax * cy) < 0;

中间的乘法是一个快捷方式，用于：

return Sign(ay * bx - ax * by) != Sign(ay * cx - ax * cy);

没有复数，这个问题也可以看作向量B是 { Rcos beta, Rsin beta }，可以用旋转矩阵表示。

R*[  cb -sb ]    [ bx -by ],   cb = cos(beta), sb = sin(beta)
  [  sb  cb ] =  [ by  bx ]    cos(-beta) = cos(beta), sin(-beta) = -sin(beta)

使用缩放矩阵[bx by, -by bx]的转置来乘以[ax,ay]，[cx,cy]会对[ax, ay]* rotMatrix(-beta)，[cx, cy]* rotMatrix(-beta)的长度产生完全相同的影响。

- Aki Suihkonen

---

投影不需要计算向量的大小吗？ - user1759679

他们通常会这样做。但我认为，等式的左侧乘以|A||B||A||C|，右侧乘以|A||C||A||B|。 - Aki Suihkonen

乘法方法是正确的，因为如果B与A或C重合，则乘积将为零。 - Aki Suihkonen

虚数和共轭一直不是我的强项，所以我很难理解。但是你给了我一个很好的想法，如果将向量B设置为我们坐标空间轴之一，那么问题就变得非常简单了。只需要进行两次矩阵旋转，然后比较符号即可。我会花一些时间来尝试一下这个方法。 - user1759679

Answer 3

在极坐标系中，你只需要问 θ_A < θ_B < θ_C 是否成立。因此首先进行极坐标转换：

a_theta = ax ? atan(ay / ax) : sign(ay) * pi

- Phil H

---

这基本上是与我的答案相同的几何解释，顺便提一下，它可以自动处理零。 - Aki Suihkonen

A和C是可以互换的，且它们没有从左到右的定义和已知顺序。虽然这很容易解决，但更大的问题是如果B被反转，它似乎会返回true。 - user1759679

抱歉，我有一个更长的答案，但是初始近似存在缺陷，所以我现在删除了其余部分。一般的想法是使用一个更便宜的等价物来代替单调递增的索引，并在其上进行比较。 - Phil H