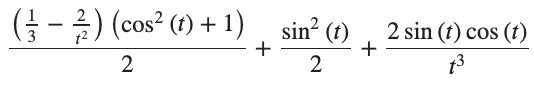NumPy数组精度提高

Question

我有一个简单的函数需要评估。

def f0(wt):
    term1 = (1 + np.cos(wt)**2) * (1 / 3 - 2 / (wt)**2)
    term2 = np.sin(wt)**2
    term3 = 4 / (wt)**3 * np.cos(wt) * np.sin(wt)
    return 0.5 * (term1 + term2 + term3)

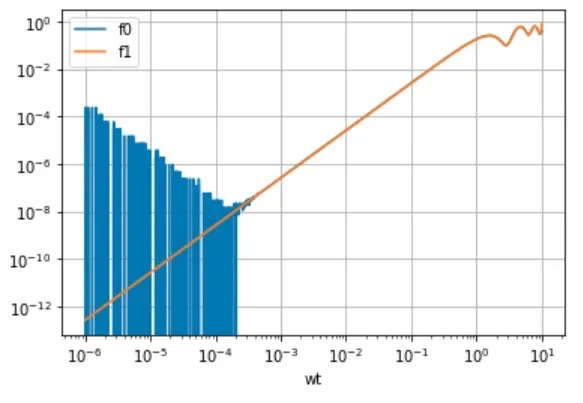
对于wt的小值（约为1e-4及以下），我在函数评估中似乎存在数值问题。事实上，term1和term3具有非常大而且几乎相反的值，但term2非常小。

我认为通过将这三个术语的总和分成两部分，如此处所示，我稍微改进了一些东西。

def f1(wt):
    # Split the calculation to have more stability hopefully
    term1 = (1 + np.cos(wt)**2) * (1 / 3 - 2 / (wt)**2)
    term2 = np.sin(wt)**2
    term3 = 4 / (wt)**3 * np.cos(wt) * np.sin(wt)
    partial = term1 + term3
    return 0.5 * (partial + term2)

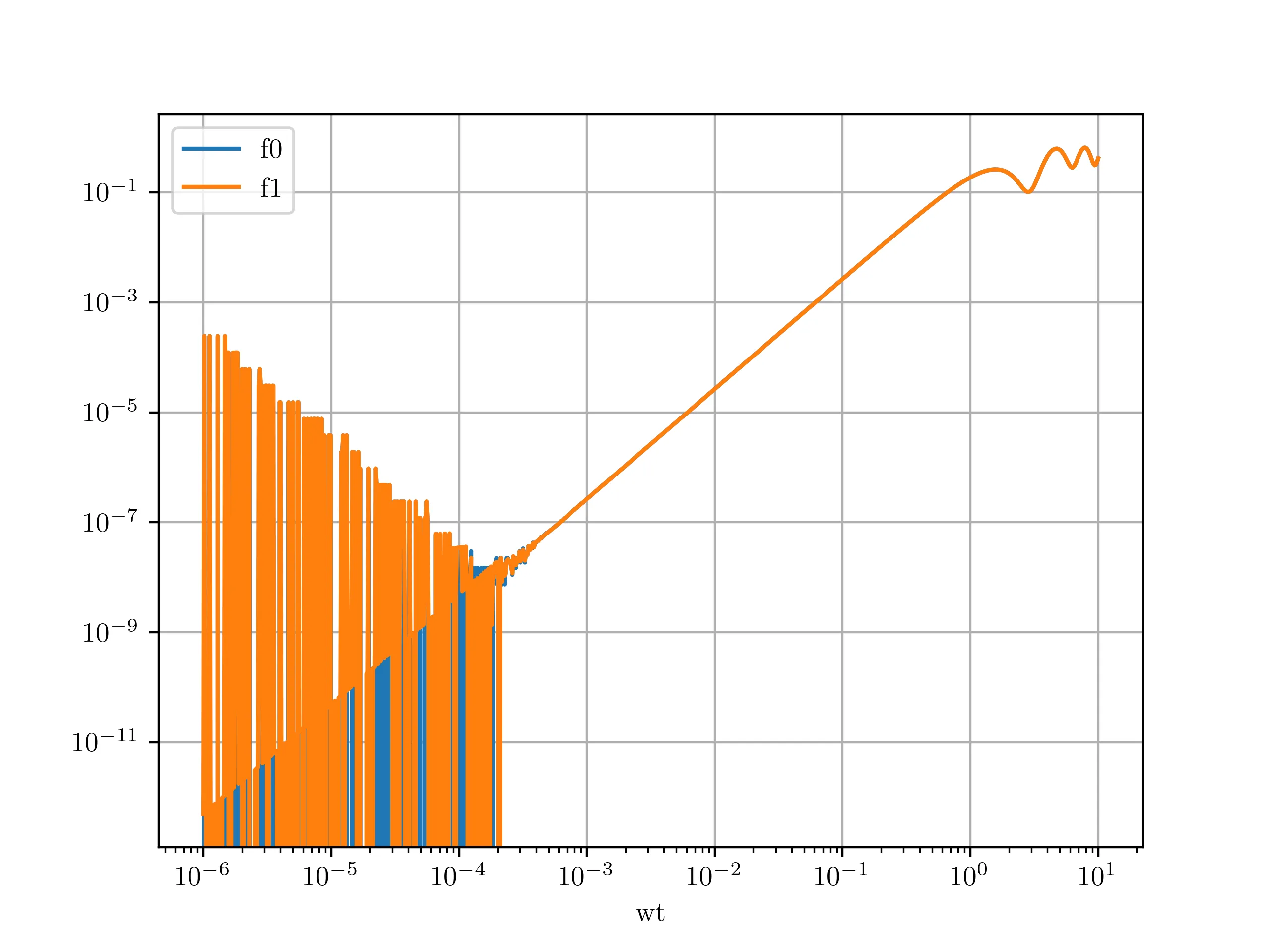
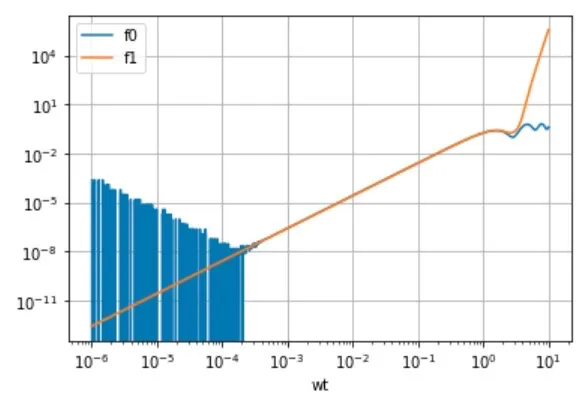
然而，对于非常小但正的wt值，我认为仍然存在数值问题。我期望此函数对于任何正值的wt都是平滑的，但是，如您所见，从附加的绘图中可以看到，在1e-3以下的值存在不连续的异常情况。

我的问题是：如果我已经使用了float64数据类型，那么如何提高Numpy的数值精度？

注意：我使用的是64位Windows 10机器。我在其他Stack Overflow线程上读到，类np.float128不可用。

完整代码片段

import numpy as np
import matplotlib.pyplot as plt

wt = np.logspace(-6, 1, 1000)

def f0(wt):
    term1 = (1 + np.cos(wt)**2) * (1 / 3 - 2 / (wt)**2)
    term2 = np.sin(wt)**2
    term3 = 4 / (wt)**3 * np.cos(wt) * np.sin(wt)
    return 0.5 * (term1 + term2 + term3)

def f1(wt):
     # Split the calculation to have more stability hopefully
     term1 = (1 + np.cos(wt)**2) * (1 / 3 - 2 / (wt)**2)
     term2 = np.sin(wt)**2
     term3 = 4 / (wt)**3 * np.cos(wt) * np.sin(wt)
     partial = term1 + term3
     return 0.5 * (partial + term2)

plt.figure()
plt.loglog(wt, f0(wt), label='f0')
plt.loglog(wt, f1(wt), label='f1')
plt.grid()
plt.legend()
plt.xlabel('wt')
plt.show()

- Davide Dal Bosco

---

我认为问题不在于改进Numpy的精度（这最终取决于您的机器和底层数学例程的精度），而是集中于实现此函数，这可能需要针对小值等恼人的特殊情况进行处理。 - Iguananaut

Answer 1

您可以用正弦和余弦的泰勒级数的前几项来代替它们。然后sympy可以给您一个简单的结果，希望在数值上更适合。

首先，我稍微更改了您的函数，以便它给出一个sympy表达式。

from sympy import *
t = symbols('t')

def f0(wt):
    term1 = (1 + sympy.cos(wt)**2) * (sympy.Rational(1,3) - 2 / (wt)**2)
    term2 = sympy.sin(wt)**2
    term3 = 4 / (wt)**3 * sympy.cos(wt) * sympy.sin(wt)
    return sympy.Rational(1,2)*(term1 + term2 + term3)
expr = f0(t)
expr

现在我将sin和cos替换为它们的泰勒多项式。

def taylor(f, n):
    return sum(t**i/factorial(i) * f(t).diff(t, i).subs(t,0) for i in range(n))

tsin = taylor(sin, 7)
tcos = taylor(cos, 7)

expr2 = simplify(expr.subs(sin(t),tsin).subs(cos(t),tcos))
f1 = lambdify(t, expr2, 'numpy')
expr2

最后，我使用您的代码进行绘图。请注意，我使用了 sympys 选项来创建一个 numpy ufunc。

wt = np.logspace(-6, 1, 1000)
plt.figure()
plt.loglog(wt, f0(wt), label='f0')
plt.loglog(wt, f1(wt), label='f1')
plt.grid()
plt.legend()
plt.xlabel('wt')
plt.show()

显然，这个函数只在零附近和1到10之间的值才有效，你应该采用原始函数。但是，如果您需要说服别人并且不关心使用替换泰勒多项式的函数看起来很好，您可以将度数提高到25，使其在至少10处视觉上与您的函数一致。

您可以组合这些函数，这样它就会使用我的函数计算零附近的值，而使用您的函数计算其他值，如下所示。

def f2(wt):
    cond = np.abs(wt) > 1/10
    return np.piecewise(wt, [cond, ~cond], [f0,f1])

- Lukas S

Answer 2

您面临的问题是灾难性的抵消，不能使用更高的精度来解决该问题，因为这样通常会推迟实际问题的解决。问题的根源是数值不稳定性，必须通过重新构造数学表达式来解决。 请注意，f1比f0好一点，但抵消问题出现在term1 + term3中。

通过对表达式进行简单的展开/分解操作和使用三角恒等式，可以得到以下函数：

def f2(wt):
     sw = np.sin(wt)
     sw2 = np.sin(2*wt)
     return (sw/wt)**2 + 1/3 + (sw2 / wt - 2) / wt**2 + sw**2 / 3

这个函数更加准确，但仍然存在一个引起相同问题的取消。这是因为表达式 E = (sw2 /wt - 2) / wt**2 是问题的根源。事实上，当 wt 接近 0 时，np.sin(2*wt) 趋近于 2。因此，sw2 / wt - 2 接近于 0，表达式 E 在接近于零的值除以另一个接近于零的值时数值不稳定。如果可以通过解析重构E来消除奇点，那么得到的表达式很可能是数值稳定的。有关更多信息，请查看 sinc function 和 how to compute an approximation 的相关内容（也可在Numpy中使用）。

一种简单的解决方法是使用像Taylor series这样的数值工具。由于其导数，Taylor级数可以准确地近似计算出 E 表达式在接近零时的值。实际上，人们可以使用Taylor级数来计算整个表达式，而不仅仅是E。但是，对于接近1的值使用Taylor级数会得到不准确的结果。事实上，该方法的精度在超过1后很快下降。一种解决方案是只对小值使用Taylor级数。

以下是最终的实现：

def f3(wt):
     sw = np.sin(wt)
     sw2 = np.sin(2*wt)
     reference = (sw/wt)**2 + 1/3 + (sw2 / wt - 2) / wt**2 + sw**2 / 3
     # O(13) Taylor series computation used only for near-zero values
     taylor = (  (  4. /        15.) * wt**2
               - ( 29. /       315.) * wt**4
               + ( 37. /      2835.) * wt**6
               - (151. /    155925.) * wt**8
               + (268. /   6081075.) * wt**10
               - (866. / 638512875.) * wt**12)
     # Select the best implementation
     return np.where(np.logical_and(wt >= -0.2, wt <= 0.2), taylor, reference)

这个实现在实践中非常精确（精度>=12位数），同时速度相对较快。以下是结果:

- Jérôme Richard