基于两个已知点（已知半径），使用求解/优化方法确定圆心

Question

我有一对点，想要找到由这两个点确定的已知半径圆。我将在模拟中使用它，并且可能会有限制条件，例如x和y的取值范围（比如一个-200到200的矩形）。

据已知，半径的平方为

(x-x1)^2 + (y-y1)^2 = r^2
(x-x2)^2 + (y-y2)^2 = r^2

我现在希望解决这个非线性方程组，以得到两个可能的圆心。我尝试使用BB软件包。这是我薄弱的尝试，只给出了一个点。我想要的是得到两个可能的点。任何指向正确方向的提示都会受到第一次可能机会的免费啤酒赞赏。

library(BB)
known.pair <- structure(c(-46.9531139599816, -62.1874917150412, 25.9011462171242, 
16.7441676243879), .Dim = c(2L, 2L), .Dimnames = list(NULL, c("x", 
"y")))

getPoints <- function(ps, r, tr) {
    # get parameters
     x <- ps[1]
     y <- ps[2]
                
     # known coordinates of two points
     x1 <- tr[1, 1]
     y1 <- tr[1, 2]
     x2 <- tr[2, 1]
     y2 <- tr[2, 2]
                
     out <- rep(NA, 2)
     out[1] <- (x-x1)^2 + (y-y1)^2 - r^2
     out[2] <- (x-x2)^2 + (y-y2)^2 - r^2
     out
}

slvd <- BBsolve(par = c(0, 0),
                fn = getPoints,
                method = "L-BFGS-B",
                tr = known.pair,
                r = 40
                )

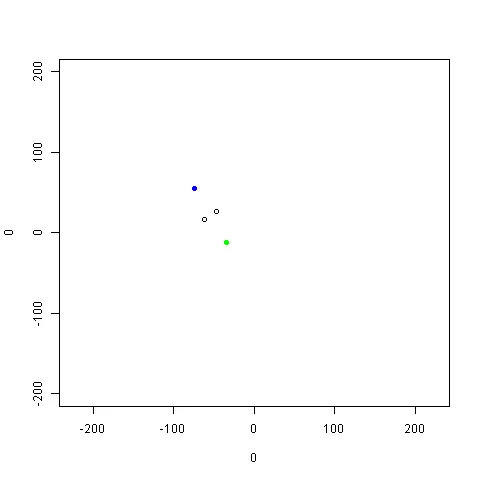
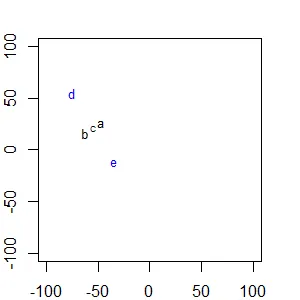
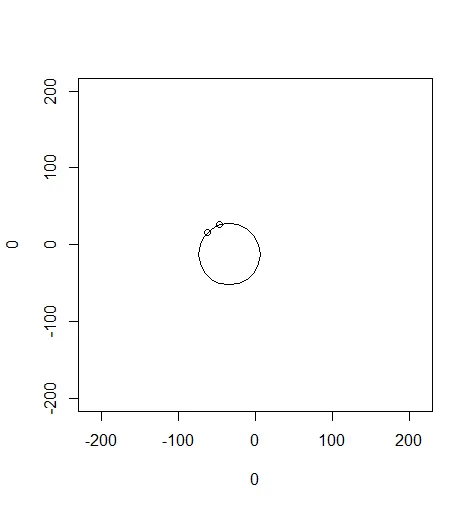
从图形上看，你可以通过以下代码看到这一点，但你需要额外的软件包。

library(sp)
library(rgeos)
plot(0,0, xlim = c(-200, 200), ylim = c(-200, 200), type = "n", asp = 1)
points(known.pair)
found.pt <- SpatialPoints(matrix(slvd$par, nrow = 1))
plot(gBuffer(found.pt, width = 40), add = T)

补充说明

感谢大家提供宝贵的评论和代码。我会提供回复者回答问题所需的时间，并附上他们的代码。

    test replications elapsed relative user.self sys.self user.child sys.child
4   alex          100    0.00       NA      0.00        0         NA        NA
2  dason          100    0.01       NA      0.02        0         NA        NA
3   josh          100    0.01       NA      0.02        0         NA        NA
1 roland          100    0.15       NA      0.14        0         NA        NA

- Roman Luštrik

---

这些点是否在圆周上？ - James

可以通过手工解方程组并使用公式来解决问题。 - MBo

@James，是的，这些点位于圆周上。我已经更新了我的答案，展示了结果。 - Roman Luštrik

Answer 1

下面的代码将为您获取两个所需圆的中心点。现在没有时间对此进行评论或将结果转换为Spatial*对象，但这应该可以为您提供一个好的开始。 首先，这是一个ASCII艺术图表，用于介绍点名称。k和K是已知点，B是通过k绘制的水平线上的一个点，C1和C2是您要寻找的圆的中心：

        C2





                            K


                  k----------------------B






                                       C1

现在来看代码：

# Example inputs
r <- 40
known.pair <- structure(c(-46.9531139599816, -62.1874917150412, 
25.9011462171242, 16.7441676243879), .Dim = c(2L, 2L), 
.Dimnames = list(NULL, c("x", "y")))

## Distance and angle (/_KkB) between the two known points
d1 <- sqrt(sum(diff(known.pair)^2))
theta1 <- atan(do.call("/", as.list(rev(diff(known.pair)))))

## Calculate magnitude of /_KkC1 and /_KkC2
theta2 <- acos((d1/2)/r)

## Find center of one circle (using /_BkC1)
dx1 <- cos(theta1 + theta2)*r
dy1 <- sin(theta1 + theta2)*r
p1 <- known.pair[2,] + c(dx1, dy1)

## Find center of other circle (using /_BkC2)
dx2 <- cos(theta1 - theta2)*r
dy2 <- sin(theta1 - theta2)*r
p2 <- known.pair[2,] + c(dx2, dy2)

## Showing that it worked
library(sp)
library(rgeos)
plot(0,0, xlim = c(-200, 200), ylim = c(-200, 200), type = "n", asp = 1)
points(known.pair)
found.pt <- SpatialPoints(matrix(slvd$par, nrow = 1))
points(p1[1], p1[2], col="blue", pch=16)
points(p2[1], p2[2], col="green", pch=16)

- Josh O'Brien

Answer 2

这是解决它的基本几何方法，其他所有人都在提到它。 我使用polyroot获取生成的二次方程的根，但您也可以直接使用二次方程。

# x is a vector containing the two x coordinates
# y is a vector containing the two y coordinates
# R is a scalar for the desired radius
findCenter <- function(x, y, R){
    dy <- diff(y)
    dx <- diff(x)
    # The radius needs to be at least as large as half the distance
    # between the two points of interest
    minrad <- (1/2)*sqrt(dx^2 + dy^2)
    if(R < minrad){
        stop("Specified radius can't be achieved with this data")
    }

    # I used a parametric equation to create the line going through
    # the mean of the two points that is perpendicular to the line
    # connecting the two points
    # 
    # f(k) = ((x1+x2)/2, (y1+y2)/2) + k*(y2-y1, x1-x2)
    # That is the vector equation for our line.  Then we can
    # for any given value of k calculate the radius of the circle
    # since we have the center and a value for a point on the
    # edge of the circle.  Squaring the radius, subtracting R^2,
    # and equating to 0 gives us the value of t to get a circle
    # with the desired radius.  The following are the coefficients
    # we get from doing that
    A <- (dy^2 + dx^2)
    B <- 0
    C <- (1/4)*(dx^2 + dy^2) - R^2

    # We could just solve the quadratic equation but eh... polyroot is good enough
    k <- as.numeric(polyroot(c(C, B, A)))

    # Now we just plug our solution in to get the centers
    # of the circles that meet our specifications
    mn <- c(mean(x), mean(y))
    ans <- rbind(mn + k[1]*c(dy, -dx),
                 mn + k[2]*c(dy, -dx))

    colnames(ans) = c("x", "y")

    ans
}

findCenter(c(-2, 0), c(1, 1), 3)

- Dason

Answer 3

跟随@PhilH的解决方案，使用R中的三角函数：

radius=40

在半径上绘制原始点

plot(known.pair,xlim=100*c(-1,1),ylim=100*c(-1,1),asp=1,pch=c("a","b"),cex=0.8)

找到线段ab的中点c(即两个圆心de的中点)

AB.bisect=known.pair[2,,drop=F]/2+known.pair[1,,drop=F]/2
C=AB.bisect
points(AB.bisect,pch="c",cex=0.5)

找到弦ab的长度和角度

AB.vector=known.pair[2,,drop=F]-known.pair[1,,drop=F]
AB.len=sqrt(sum(AB.vector^2))
AB.angle=atan2(AB.vector[2],AB.vector[1])
names(AB.angle)<-NULL

计算从c到两个圆心的线段长度和角度

CD.len=sqrt(diff(c(AB.len/2,radius)^2))
CD.angle=AB.angle-pi/2

计算并绘制垂线到 ab 上的两个中心点 d 和 e 的位置，并给出长度：

center1=C+CD.len*c(x=cos(CD.angle),y=sin(CD.angle))
center2=C-CD.len*c(x=cos(CD.angle),y=sin(CD.angle))
points(center1[1],center1[2],col="blue",cex=0.8,pch="d")
points(center2[1],center2[2],col="blue",cex=0.8,pch="e")

展示：

- Alex Brown

Answer 4

无需求解任何数值方程，只需要应用下列公式：

1. 因为点A和B均位于圆上，所以它们与给定圆心的距离均为半径r。
2. 以两个已知点的弦为底，第三个点为圆心构成等腰三角形。
3. 将该等腰三角形从A和B中点处平分，得到一个直角三角形。
4. 根据http://mathworld.wolfram.com/IsoscelesTriangle.html，可以用底边长和半径来计算高度。
5. 按照AB弦的法线方向(参见此SO答案)，在每个方向上沿着刚刚计算出的高度距离前进。

- Phil H

Answer 5

以下是一个答案的骨架，如果我有时间，我会详细说明。如果你跟着这些话画图，应该很容易理解，抱歉我在这台电脑上没有正确的软件为你画出图片。

忽略那些点相同（无限解）或者太远而不能落在你选择的半径相同的圆上（无解）的退化情况。

标记点为X和Y，两个圆的未知中心点为c1和c2。c1和c2位于XY的垂直平分线上；将其称为c1c2线，在这个阶段我们不知道c1和c2的位置细节也没关系。

因此，找出线段c1c2的方程。它通过XY的中点（称为点Z），并且具有与XY负倾斜率相等的斜率。现在你有了c1c2的方程（如果这些骨头上有肉的话）。

现在从一个点构建三角形，该点是线段及其垂直平分线的交点和圆的中心点（例如XZc1）。你仍然不知道c1的确切位置，但这从未阻止过任何人勾画几何图形。你有一个已知两个边长的直角三角形（XZ和Xc1），因此很容易找到Zc1。对于另一个三角形和圆心，重复此过程。

当然，这种方法与OP最初的方法非常不同，可能不会吸引人。

- High Performance Mark

Answer 6

有一些警告需要解决，但这应该可以让您开始了。可能会存在性能问题，因此使用基本几何完全解决它可能是更好的方法。

known.pair <- structure(c(-46.9531139599816, -62.1874917150412, 25.9011462171242, 
                          16.7441676243879), .Dim = c(2L, 2L), .Dimnames = list(NULL, c("x", 
                                                                                        "y")))

findCenter <- function(p,r) {
  yplus <- function(y) {
    ((p[1,1]+sqrt(r^2-(y-p[1,2])^2)-p[2,1])^2+(y-p[2,2])^2-r^2)^2
  }


 yp <- optimize(yplus,interval=c(min(p[,2]-r),max(p[,2]+r)))$minimum
 xp <- p[1,1]+sqrt(r^2-(yp-p[1,2])^2)  
 cp <- c(xp,yp)
 names(cp)<-c("x","y") 

 yminus <- function(y) {
   ((p[1,1]-sqrt(r^2-(y-p[1,2])^2)-p[2,1])^2+(y-p[2,2])^2-r^2)^2
 }


 ym <- optimize(yminus,interval=c(min(p[,2]-r),max(p[,2]+r)))$minimum
 xm <- p[1,1]-sqrt(r^2-(ym-p[1,2])^2)  
 cm <- c(xm,ym)
 names(cm)<-c("x","y")


 list(c1=cp,c2=cm)
}

cent <- findCenter(known.pair,40)

- Roland

Answer 7

我希望你了解一些基本的几何知识，因为我不幸不能画它。

垂直平分线是这样一条线：通过两点A和B的圆的每个中点都在该线上。

现在你有AB的中点和r，所以你可以用点A、AB中点和圆的未知中点绘制一个直角三角形。

现在使用勾股定理来获得AB中点到圆中点的距离，并使用基本的正弦/余弦组合来计算圆的位置不应该很难。

- unddoch