寻找线段和贝塞尔曲线相交的程序

Question

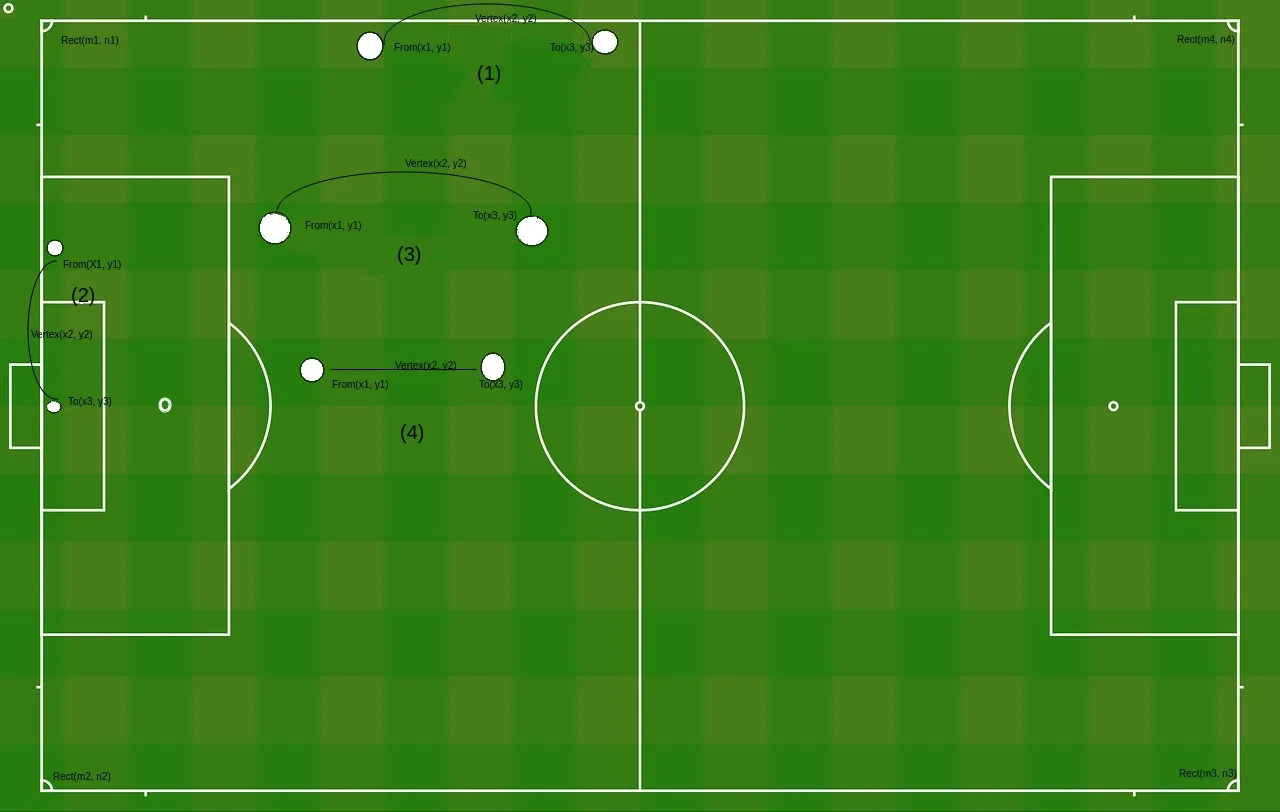
考虑以下足球场地的图片：

从图片中可以看到各种球的运动，其中一些是弯曲的（即图像中的 (1), (2), (3)），而有些则不是（如线条(4)）。

因此，我需要找出球路径与球门线和侧线的交点。有时输入可能不是曲线（比如图像中的(4)）。

我已经编写了一个程序，但我不知道哪里出了问题——这是解决这种问题的正确方法吗？

如果是，那么如何将贝塞尔曲线转换为方程以便更好地解决问题？

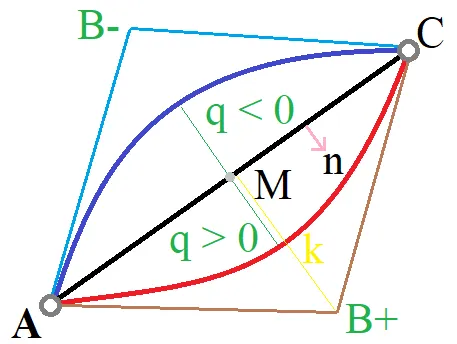
考虑给定条件：

beizer curve eqaution -> a(x*x) + b*x + c
and line segment equation -> y = y1 + m(x-x1)

//maxCurvedPoint是曲线的最高点

var getIntersectionPoint = function (room, ballFromPosition, ballToPosition, maxCurvePoint) 
{
    var linepoints = [[m1,n1], [m2, n2], [m3, n3], [m4, n4]];

    //converting three points(ballFromPosition, maxCurvePoint, ballToPosition) into the quadratic equation (Bezier curve) --(1)
    //getting the equation of the line segment using the linepoints --(2)

    //equating (1) and (2) and getting a quadratic equation and solving and finding intersection points
    return intersectionPoint;
}

// solves //(-b(+-)sqrt(b*b - 4ac)/2ac)
function solve(a, b, c) 
{        
 //check curve intersects line or not
   if((Math.pow(b, 2) - (4 * a * c)) >= 0) 
   {
       result1 = (-1 * b + Math.sqrt(Math.pow(b, 2) - (4 * a * c))) / (2 * a);
       result2 = (-1 * b - Math.sqrt(Math.pow(b, 2) - (4 * a * c))) / (2 * a);
       return [result1, result2];
   } 

   return [];
}

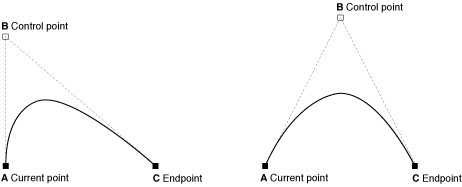
有人能帮我解决这个问题吗？同时，曲线上最高点是否可以称为曲线的顶点？

- paradox

---

你可能会得到一个输出，因为这个方程描述了一个无限的抛物线，而你的“抛物线”只是这些无限抛物线的部分。你应该检查交点坐标范围。 - meowgoesthedog

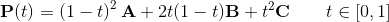
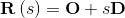
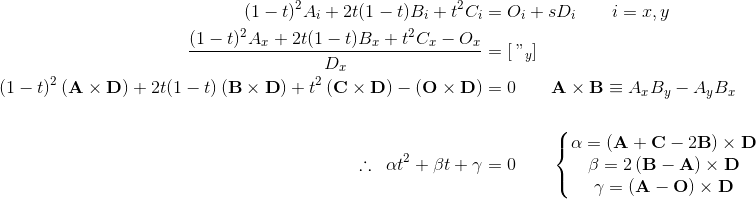
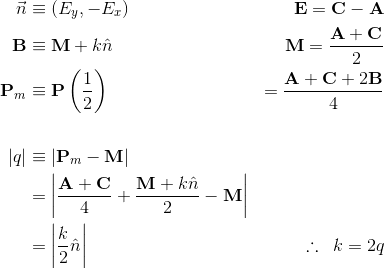
两个建议，第一个是通过使用辅助函数使代码更易读（例如 const square = n => Math.pow(n, 2); 而不是内联所有的数学计算），第二个是由于 JavaScript 语言的一个特殊性，强烈推荐使用 K&R 风格的大括号而不是 GNU 风格的大括号。我敢打赌，如果你至少做到第一个建议，很可能会发现你的问题所在。 - Jared Smith

你应该首先了解参数曲线方程的概念。 - user1196549

Answer 1

我发现使用向量方程更容易工作，因为代数是旋转不变的（因此您不必重新编写代码来处理例如“水平”抛物线）。

---

1.曲线表示+交点测试

考虑一个具有端点A、C，控制点B和参数t的二次贝塞尔曲线：

以及具有源O、方向D和参数s的无限直线：

将P和R等式化得到一组二次联立方程，可以重新排列以消除s并找到抛物线参数t：

解这个二次方程，只接受范围在[0,1]内的实根。这确保任何交点始终在段本身上。

---

2.处理线段

您还可以通过使用上述方程计算s从t，限制其值（如果D已归一化，则等于沿线的距离）来将交点限制为线段。

---

3.计算控制点B

请注意，一般情况下的控制点B的值不会给出对称的抛物线。要计算一般对称曲线的B：

定义变量：

• M: AB的中点
• n: 沿着AC方向的顺时针法线
• q: M到曲线中点的距离为有符号凸度距离
• k: M到B的距离为有符号距离

一个惊人简单的结果。

---

4. C#样例代码

public static Vector2[] computeIntersection
(
   Vector2 A, Vector2 C, double q,    // parabola segment
   Vector2 O, Vector2 P               // line segment
)
{
   // quadratic solve
   double[] solve(double a, double b, double c)
   {
      double d = b * b - 4.0 * a * c;
      if (d < 0.0) // imaginary roots - no intersection at all
         return null;

      if (d > 0.0) // two distinct real roots
      {
         double sd = Math.Sqrt(d);
         return new double[2] { (-b + sd) / (2.0 * a),
                                (-b - sd) / (2.0 * a) };
      }
      else // only one (line segment is tangent to curve)
      {
         return new double[1] { -b / (2.0 * a) };
      }
   }

   // cross product (in-case undefined)
   double cross(Vector2 i, Vector2 j)
   {
      return i.x * j.y - i.y * j.x;
   }

   // validity check for t and s
   bool valid(double v)
   {
      return (v >= 0.0) && (v <= 1.0);
   }

   // compute control point B
   Vector2 E = C - A;
   Vector2 M = 0.5 * (A + C);
   Vector2 N = (new Vector2(E.y, -E.x)).normalize();
   Vector2 B = M + (2.0 * q) * N;

   // solving for t
   Vector2 D = P - O;
   bool useX = Math.Abs(D.X) > Math.Abs(D.Y);
   double[] T = solve(cross(A + C - 2.0 * B, D),
                      cross(B - A, D) * 2.0,
                      cross(A - O, D));
   if (T == null) return null;

   Vector2[] I = new Vector2[2];
   int c = 0;

   for (int i = 0; i < T.Length; i++)
   {
      // check if t is within curve range
      double t = T[i];
      if (!valid(t)) continue;

      // solve for s and check if is within line range
      double u = (1 - t) * (1 - t);
      double v = 2 * t * (1 - t);
      double w = t * t;
      double s = useX ? ((u * A.X + v * B.X + w * C.X - O.X) / D.X)
                      : ((u * A.Y + v * B.Y + w * C.Y - O.Y) / D.Y);
      if (!valid(s)) continue;

      // compute the corresponding intersection point
      I[c++] = O + s * D;
   }

   // only return valid solutions
   if (c == 0) return null;
   Array.Resize(ref I, c);
   return I;
}

- meowgoesthedog

---

@meowgoesthedog，谢谢回复，但是我没有控制点，只有曲线的顶点，有没有办法获取控制点呢？ - paradox

@meowgoesthedog，如果不是无限线而是线段的话，那么在这种情况下 - paradox

@meowgoesthedog，请问你能否粘贴一下示例代码？ - paradox

@paradox 你想先尝试一下吗？如果你卡住了，我可以贴一些代码，但是这些方程式很简单实现。另外，你接受用其他语言编写的代码吗，比如Java / C#？我对JS有点生疏了。 - meowgoesthedog

@paradox 我更新了示例代码，希望如果你卡住了能有所帮助。 - meowgoesthedog

Answer 2

如果您将所有端点进行平移和旋转，使得线段变为(0, 0)-(d, 0)，问题就简化了。

设控制点为(Xk, Yk)，其中k= 0, 1, 2。通过解二次方程式来求解与X轴的交点的t值。

Y0 (1-t)² + 2 Y1 t(1-t) + Y2 t² = 0.

相应的横坐标由以下给出

X0 (1-t)² + 2 X1 t(1-t) + X2 t² = 0.

你可以检查这些是否属于区间 [0, d]。然后应用反向旋转和平移。

---

附加说明：两个二次贝塞尔曲线的交点

其中一个曲线的向量方程可以写成：

P = P0 (1 - t)² + 2 P1 t (1 - t) + P2 t²
  = P0 + 2 (P1 - P0) t + (P0 - 2 P1 + P2) t².

如果您应用仿射坐标变换，使参考框架变为(P0，P1-P0，P0-2 P1 + P2)，则方程式简化为：

X = 2t
Y = t²

这是隐式方程

X² = 4Y.

现在将相同的变换应用于第二条曲线的控制点，并将参数方程代入上述公式，您会得到一个关于t的四次方程（一边是二次多项式的平方，另一边是二次多项式）。

有关四次方程根的闭合形式公式，可能有四个根。在选择[0,1]中的实根后，您需要评估第一条曲线的t参数，并检查其是否属于[0,1]。

不要忘记恢复原始坐标。

- user1196549