假设我想在一个凸多边形内均匀采样点。
其中最常见的方法是对该多边形进行三角剖分,然后使用不同的方案在每个三角形中生成均匀随机点。
我发现其中最实用的一种方法是通过从均匀分布中生成指数分布,例如取-log(U),并将总和归一化为1。
在Matlab中,我们可以使用以下代码在三角形内均匀采样:
vertex=[0 0;1 0;0.5 0.5]; %vertex coordinates in the 2D plane
mix_coeff=rand(10000,size(vertex,1)); %uniform generation of random coefficients
x=-log(x); %make the uniform distribution exponential
x=bsxfun(@rdivide,x,sum(x,2)); %normalize such that sum is equal to one
unif_samples=x*vertex; %calculate the 2D coordinates of each sample inside the triangle
这很有效:
然而,对于除了三角形以外的任何东西,完全相同的方案都会失败。例如对于一个四边形,我们得到以下结果:
显然,采样不再均匀,顶点越多,越难“到达”这些顶点。
如果我先将多边形三角化,那么在每个三角形中进行均匀采样就很容易,很明显可以完成任务。
但是为什么?为什么需要先三角化?
具有哪些特性的三角形(和一般的simplex,因为这种行为似乎扩展到n维构造)使其对它们有效而对其他多边形无效?
如果有人能给我一个直观的解释或只是指出一些参考资料,帮助我理解发生了什么,我将不胜感激。
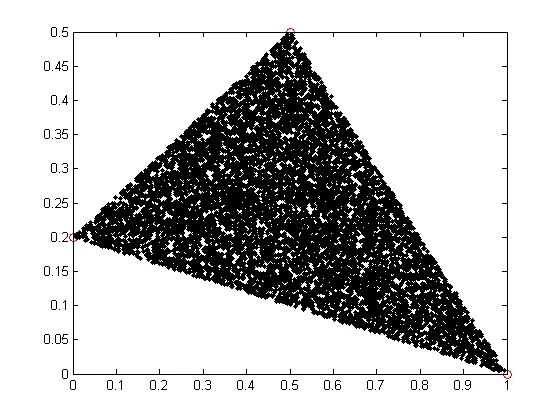
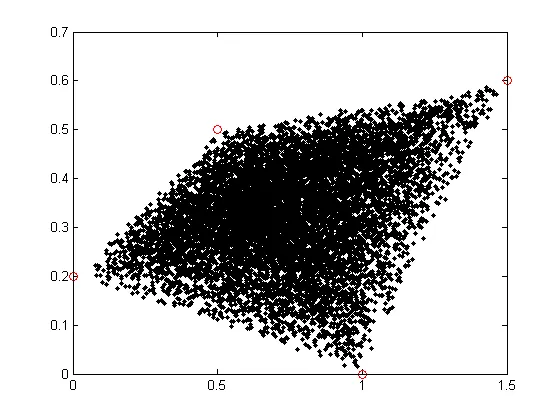
d+1中的狄利克雷分布(α=1)在满足 X1+X2+...+Xd=1 的单纯形中是均匀的。单纯形是一个三角形。在三维单纯形中,三角形平面片的角落是 (1,0,0), (0,1,0),(0,0,1)。当你将其投影到d维平面上,比如 XY 平面,你会得到三角形 (0,0),(1,0),(0,1) 中的均匀密度采样。这就是你正在做的事情,然后通过已知的顶点,你可以填充平面上的任何三角形。我们没有类似于四边形的狄利克雷分布。我想说,不可能有这样的分布来覆盖任何四边形。 - Severin Pappadeux