logo标签列表

选择具有最大相交面积的矩形

algorithmcomputational-geometry
10
在这个问题中，r是一个固定的正整数。给定平面上N个大小相同的矩形，边缘只能是垂直或水平。我们假设所有N个矩形的交集面积为非零面积。问题是如何找到N-r个矩形，以最大化交集的面积。当人们反复成像某个生物标本时，由于物理原因（例如显微镜和相机的部件差异扩大），对齐会稍微发生变化，因此在实际显微镜中会出现这个问题。我已经将问题表述为维度d=2的情况。每个d>0都有一个类似的问题。对于d=1，通过排序间隔的左端点可以获得O(N log(N))的解决方案。但让我们坚持d=2。如果r=1，则可以通过对角线坐标进行排序以在O(N log(N))的时间内再次解决该问题。
所以，是否通过先解决情况（N,1）以获得N-1个矩形，然后解决情况（N-1,1），得到N-2个矩形，一直减少到N-r个矩形来解决原始问题？我希望看到这种乐观尝试程序的明确反例。如果该程序有效（请证明！），那将更有趣。
如果r固定为某个值r>1，而N很大，这个问题是否属于NP类之一？
谢谢任何关于此的想法。
David
1
你的意思是交集指的是所有矩形共有的区域吗？ - Karoly Horvath
嗯...你的约简算法感觉不太对劲...我得想一想才能想出一个反例。 - duedl0r
8个回答
4
由于轴对齐矩形的交集是一个轴对齐矩形，因此可能的交集有O(N4)个（O(N)左侧，O(N)右侧，O(N)顶部，O(N)底部）。明显的O(N5)算法是尝试所有这些交集，并检查每个交集是否至少被N-r个矩形所包含。
O(N3)的改进是在X维度中尝试所有O(N2)个间隔，并在包含给定X间隔的矩形上在Y维度上运行1D算法。（矩形只需要排序一次。）
N有多大？我认为精美的数据结构可能会导致O(N2 log N)算法，但如果立方体算法足够，那么它不值得你花时间。
2
我认为我有一个反例。假设您有r := N-2。也就是说，您想查找最大重叠的两个矩形。假设您有两个覆盖相同面积（=最大重叠）的矩形。这两个将最终成为最佳结果。
现在我们需要构造更多的矩形，以便其中至少一个被删除。
假设我们有三个重叠很多的矩形...但它们不是最优的。它们与其他两个矩形有非常小的重叠面积。
现在，如果您要优化四个矩形的区域，则会删除其中一个最优矩形，对吗？或者也许您不必这样做，但您不确定哪个决策是最优的。
因此，我认为您的减少算法不太正确。目前我不确定是否存在有效的算法，以及这属于哪个复杂度类别。如果我有时间，我会考虑一下 :)
但是，如果在每一步中，您都排除掉提供最大N-r重叠表面的那个元素呢？在这种情况下，您可以处理(N,1)，然后是(N-1,1)等等...（这个反例在这种情况下无效） - Ricky Bobby
你能给一个完全明确的整数坐标的反例吗？这和使用实数坐标一样一般，因为你可以先用一个巨大的因子进行缩放，然后取最近的整数值。我不满意反例，除非它是完全明确的。 - David Epstein
1

附言。这个方法还有很多不足之处，但可能会激发一些想法。特别是在一个象限中存在靠近X轴和Y轴的离群值时，它们会互相加强，就像它们都在45度角上一样，将解决方案推离该象限，这种方式可能没有意义。

-

如果r比N小很多，而N又相当大，请考虑以下内容：

找到平均中心点。
按照(X-center.x)+(Y-center.y)和(X-center.x)-(Y-center.y)将矩形排序为2个序列，其中X和Y是每个矩形的中心。

对于任何解决方案，所有拒绝的矩形都将成为最多4个子序列的成员，每个子序列都是每个2个序列的头或尾。假设N比r大得多，大部分时间将用于排序序列-O(n log n)。

要找到解决方案，首先找到通过删除每个序列的头和尾处的r个矩形所给出的交集。使用此基本交集来消除您知道将在解决方案中的“核心”矩形集的考虑。这将将交集计算减少到仅使用最多4 * r + 1个矩形。

每个4个序列头和尾应与一个r个矩形的数组相关联，每个条目表示通过将“核心”与头或尾的i个最内部矩形相交所给出的交集。此预计算将将查找解决方案的复杂性从O(r^4)降低到O(r^3)。

这不是完美的，但应该很接近。
小r的缺陷可能来自于正应该被拒绝的候选对象，这些候选对象以略微更好但只在两个轴之一上的替代品存在。最大误差可能是可以计算的。如果这是一个问题，请使用真正的非交集面积计算而不是我使用的简单的“X+Y”差值公式。
谢谢。我已经独立得出了非常相似的结论。如果我现在拥有的算法（我马上会详细说明）是正确的，那么我会感到满意，因为我觉得它几乎是最好的。 - David Epstein
1

这里提供了一个明确的反例（当N=4且r=2时），来反驳提问者提出的贪心算法。

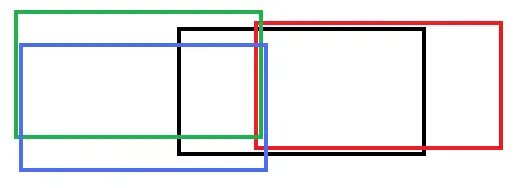
enter image description here

这些矩形中任意三个之间的最大交集在黑色、蓝色和绿色矩形之间。但是，很明显，任意两个之间的最大交集都小于黑色和红色矩形之间的交集。

非常感谢。很好的反例！正如我在原帖中所述，我确实预料到贪心算法是错误的。如果我现在拥有的算法（我马上会给出详细信息）是正确的，那么我将感到满意，因为我有一种感觉它几乎是最好的。 - David Epstein
0

我相信这会产生一个完美的解决方案。 David的解决方案更容易实现，并且在大多数情况下应该更快。

这基于这样一个假设，即对于任何解决方案，至少有一个拒绝必须是复合壳体的成员。 递归应用导致：

计算凸包。 通过以下方式收集所有候选解：

{Remove a hull member, repair the hull} r times

（上次船体实际上不需要修理。）

如果h是初始船体成员的数量，则复杂度小于h^r，再加上计算初始船体的成本。我假设选择一种船体算法，使得排序后的数据可以在船体维修中保持并重复使用。

0

我现在有一个算法，与Ed Staub的算法非常相似，具有相同的时间估计。它与Ed的有点不同，因为它适用于所有r。

mhum对贪心算法的反例很好。看一下。

0
我还在努力适应这个网站。不知何故，我之前的回答被截成了两句话。感谢所有人的贡献，特别是mhum提供的贪心算法反例令人满意。现在我有了自己的答案。我认为它尽可能好，但是复杂度的下限对我来说太难了。我的解决方案与Ed Staub的类似，并且给出了相同的复杂度估计，但适用于任何r>0的值。
我的一个矩形是由其左下角确定的。设S为左下角的集合。在O(N log(N))的时间内，我们按x坐标的大小将S排序为Sx。我们不关心具有相同x坐标的两个左下角之间的Sx顺序。类似地，使用y坐标的大小定义了排序序列Sy。现在让u1、u2、u3和u4为非负整数，其中u1+u2+u3+u4=r。当我们删除现在明确命名的各种矩形时，我们计算出面积发生的变化。我们首先删除Sx的u1大小的头部和u2大小的尾部。让Syx成为从Sy中删除这些u1+u2个条目的结果。我们删除Syx的u3大小的头部和u4大小的尾部。现在可以证明，这些(u1,u2,u3,u4)的可能选择之一给出所需的最大交集面积。(如果您想要证明细节的pdf，请给我发电子邮件。)这样的选择数量等于在4D欧几里得空间中正四面体中的整数点数，该正四面体的顶点位于坐标总和为r的4个点处，其中4个坐标中的3个等于0。这受到正四面体体积的限制，给出了O(r^3)的复杂度估计。

所以我的算法时间复杂度为O(N log(N)) + O(r^3)。

唉...我觉得这个跟我的有一样的缺陷。在这种情况下，对角线上的矩形可能是最佳选择的拒绝项，但由于它们不在最上/下/左/右的r个矩形中，所以不会被使用。我认为我的公式在这方面更加健壮，但也不完美。 - Ed Staub
@ed 我认为我的证明是正确的。如果我知道你的电子邮件，我可以写出证明并发送给你。由于我的排序仅使用一个坐标，因此极值确实是最远的上/下/左/右，无论矩形是否在对角线上。我无法确定我的电子邮件地址是否在我的个人资料中可见。 - David Epstein
-1
这只是一个想法，但如果N非常大，我可能会尝试使用蒙特卡洛算法。
思路是生成随机点（比如在所有矩形的凸包内均匀生成），并评估每个随机点的表现。如果随机点在N-r个或更多个矩形中，则更新每个子集合中N-r个矩形的命中数。
最后，具有最多随机点的N-r个矩形子集就是您的答案。
这个算法有很多缺点，其中最明显的一个是结果是随机的，因此不能保证正确性。但像大多数蒙特卡洛算法一样，它的计算规模较小，并且您应该能够将其用于更高维度的问题。
网页内容由stack overflow 提供, 点击上面的
可以查看英文原文，
原文链接