为什么对一个预转置矩阵执行矩阵乘法比对一个非转置矩阵执行更快？

Question

考虑以下 Python 代码，在其中，对一个预先转置的矩阵进行乘法运算比对一个非转置的矩阵进行乘法运算具有更快的执行时间。

import numpy as np
import time

# Generate random matrix
matrix_size = 1000
matrix = np.random.rand(matrix_size, matrix_size)

# Transpose the matrix
transposed_matrix = np.transpose(matrix)

# Multiply non-transposed matrix
start = time.time()
result1 = np.matmul(matrix, matrix)
end = time.time()
execution_time1 = end - start

# Multiply pre-transposed matrix
start = time.time()
result2 = np.matmul(transposed_matrix, transposed_matrix)
end = time.time()
execution_time2 = end - start

print("Execution time (non-transposed):", execution_time1)
print("Execution time (pre-transposed):", execution_time2)

令人惊讶的是，乘以预转置矩阵更快。也许有人会认为乘法的顺序不应该显著影响性能，但似乎确实有差别。

为什么处理预转置矩阵会导致比未转置矩阵更快的执行时间？是否有任何潜在原因或优化可以解释这种行为？

更新

我已经考虑了关于cache的评论，并且在每次循环中生成新的矩阵：

import numpy as np
import time
import matplotlib.pyplot as plt

# Generate random matrices
matrix_size = 3000



# Variables to store execution times
execution_times1 = []
execution_times2 = []

# Perform matrix multiplication A @ B^T and measure execution time for 50 iterations
num_iterations = 50
for _ in range(num_iterations):
    matrix_a = np.random.rand(matrix_size, matrix_size)
    start = time.time()
    result1 = np.matmul(matrix_a, matrix_a)
    end = time.time()
    execution_times1.append(end - start)

# Perform matrix multiplication A @ B and measure execution time for 50 iterations
for _ in range(num_iterations):
    matrix_b = np.random.rand(matrix_size, matrix_size)
    start = time.time()
    result2 = np.matmul(matrix_b, matrix_b.T)
    end = time.time()
    execution_times2.append(end - start)

# Print average execution times
avg_execution_time1 = np.mean(execution_times1)
avg_execution_time2 = np.mean(execution_times2)
#print("Average execution time (A @ B^T):", avg_execution_time1)
#print("Average execution time (A @ B):", avg_execution_time2)

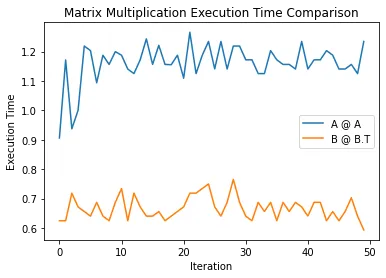
# Plot the execution times
plt.plot(range(num_iterations), execution_times1, label='A @ A')
plt.plot(range(num_iterations), execution_times2, label='B @ B.T')
plt.xlabel('Iteration')
plt.ylabel('Execution Time')
plt.title('Matrix Multiplication Execution Time Comparison')
plt.legend()
plt.show()

# Display BLAS configuration
np.show_config()

结果：

blas_mkl_info:
    libraries = ['mkl_rt']
    library_dirs = ['C:/Users/User/anaconda3\\Library\\lib']
    define_macros = [('SCIPY_MKL_H', None), ('HAVE_CBLAS', None)]
    include_dirs = ['C:/Users/User/anaconda3\\Library\\include']
blas_opt_info:
    libraries = ['mkl_rt']
    library_dirs = ['C:/Users/User/anaconda3\\Library\\lib']
    define_macros = [('SCIPY_MKL_H', None), ('HAVE_CBLAS', None)]
    include_dirs = ['C:/Users/User/anaconda3\\Library\\include']
lapack_mkl_info:
    libraries = ['mkl_rt']
    library_dirs = ['C:/Users/User/anaconda3\\Library\\lib']
    define_macros = [('SCIPY_MKL_H', None), ('HAVE_CBLAS', None)]
    include_dirs = ['C:/Users/User/anaconda3\\Library\\include']
lapack_opt_info:
    libraries = ['mkl_rt']
    library_dirs = ['C:/Users/User/anaconda3\\Library\\lib']
    define_macros = [('SCIPY_MKL_H', None), ('HAVE_CBLAS', None)]
    include_dirs = ['C:/Users/User/anaconda3\\Library\\include']
Supported SIMD extensions in this NumPy install:
    baseline = SSE,SSE2,SSE3
    found = SSSE3,SSE41,POPCNT,SSE42,AVX,F16C,FMA3,AVX2
    not found = AVX512F,AVX512CD,AVX512_SKX,AVX512_CLX,AVX512_CNL

- zoldxk

---

在我的机器上，这两个运行速度几乎相同。 - Frank Yellin

在我的机器上，这两个运行速度几乎相同。 - Frank Yellin

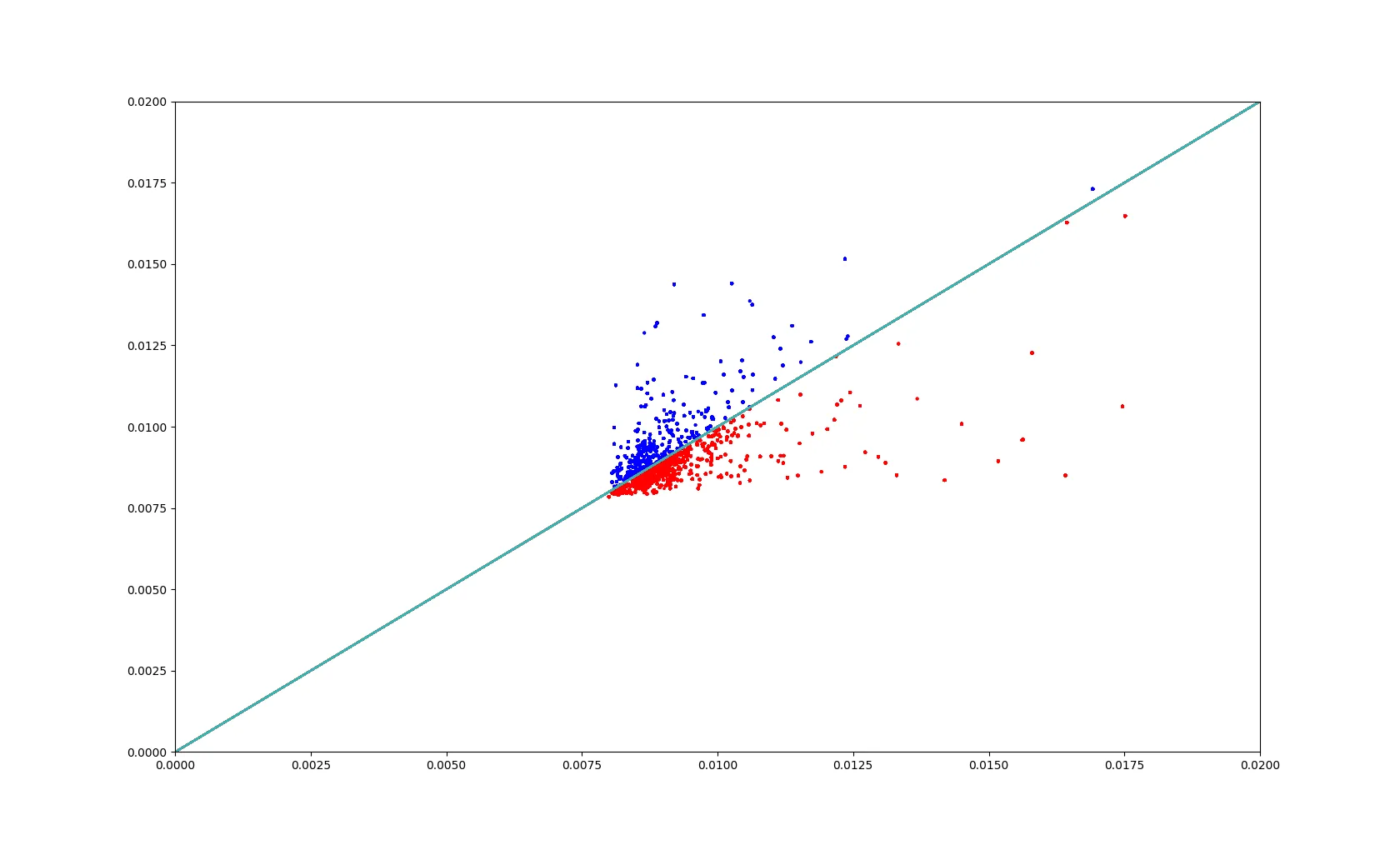
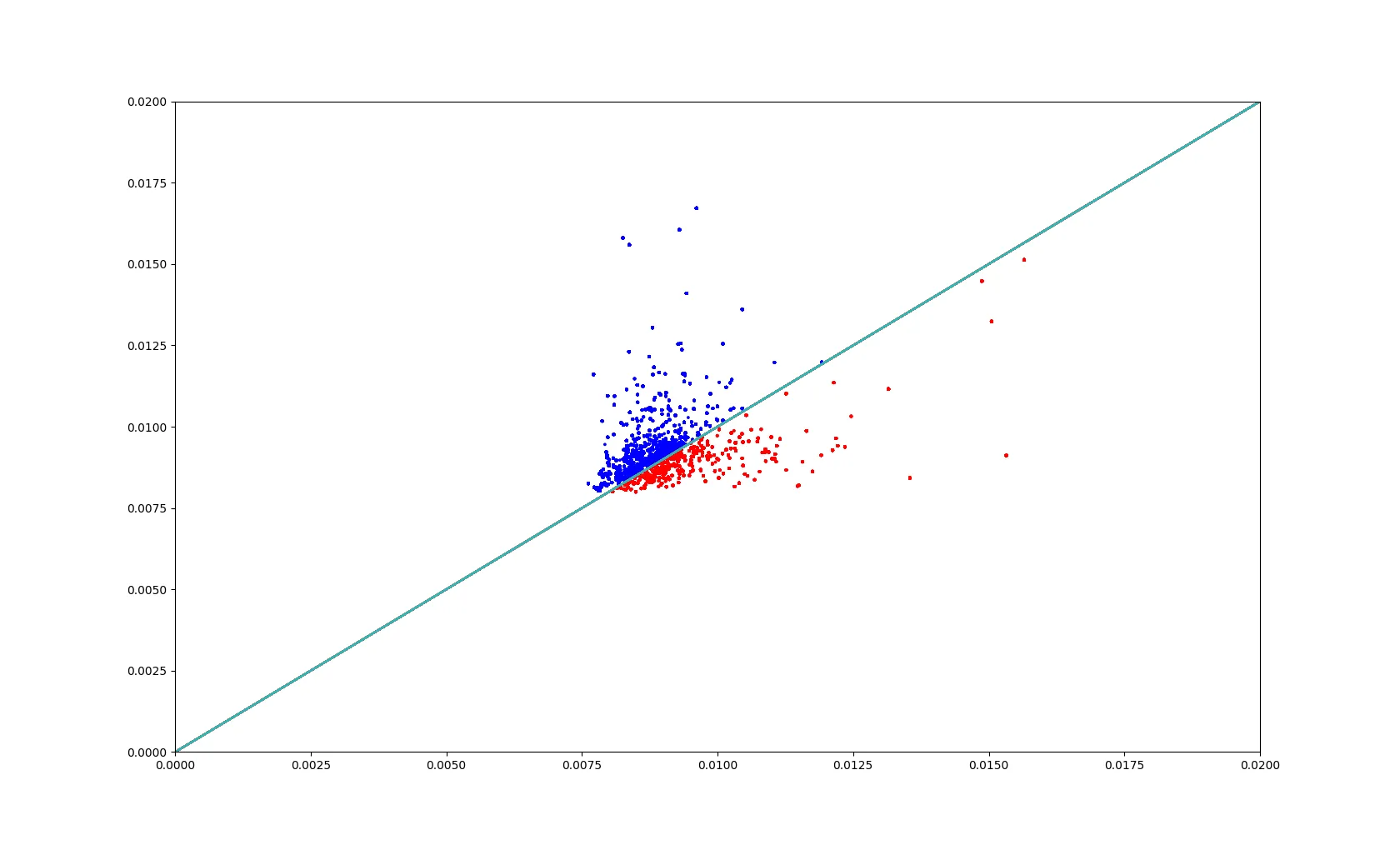
你更新的问题已经不同了。通过利用np.matmul(matrix_b, matrix_b.T)的对称性，它可以比np.matmul(matrix_a, matrix_a)快近一倍。 - max9111

你的更新问题不再是一样的了。np.matmul(matrix_b, matrix_b.T) 的结果是对称的，通过利用这个特性，它可以比 np.matmul(matrix_a, matrix_a) 快近两倍。 - max9111

你更新的问题已经不再相同了。np.matmul(matrix_b, matrix_b.T)的结果是对称的，通过利用这种行为，它可以比np.matmul(matrix_a, matrix_a)快近两倍。 - undefined

Answer 1

在我的机器上看起来并不是很明显。

进行了1000次运行。我得到了以下的时间（x=非转置，y=转置）。 红色点比蓝色点多。准确地说是685/315。所以，从p值的角度来看，毫无疑问，这不可能只是随机效应。 （抽取了1000个硬币，其中685个是正面朝上，这是一个明显的异常情况）

但从时间上来看，这并不明显。该集群主要集中在y=x轴上。

现在我开始回答是因为我相当确定这是一个缓存问题。当我还在工程学校时（很久以前，那时候这些考虑更加重要，并且由那些自己来自更加重要时代的老师教授），在高性能计算课程中，我们被教导在从Fortran切换到C时要非常小心，因为有缓存效应：当迭代数组时，按照内存中的顺序进行迭代非常重要（在numpy中仍然称为“C”顺序与“Fortran”顺序，证明它对于那些更加关注的人仍然是一个重要的考虑因素 - 我在日常工作中很少需要关心，所以我提到的是学校记忆而不是工作记忆）。

因为当处理紧挨着你刚刚处理过的数字的下一个数字时，那个数字很可能已经加载到缓存中了。而如果你处理的下一个数字是在下一行（按照C顺序，所以在内存中更远），那么它更有可能不在缓存中。在现今的缓存大小下，只有大型矩阵才会有所区别。

由于transpose不会移动任何数据，只是调整步幅，对转置矩阵进行操作的效果是改变内存中处理的数据顺序。因此，如果您考虑的是朴素算法

for i in range(N):
    for j in range(N):
        res[i,j]=0
        for k in range(N):
            res[i,j] += A[i,k] * B[k,j]

如果A和B按照C的顺序排列，那么对矩阵A的迭代是按照内存顺序完成的（我们沿着行迭代，逐列进行，因此相邻的数字在内存中一个接一个），而B则不是。

如果顺序被颠倒，例如因为它们已经转置，那么情况就相反。B按照不会引起缓存问题的顺序进行迭代，而A则不是。

好吧，不必在这个问题上花太多时间，因为我告诉你这一切只是为了解释为什么我想调查可能出现缓存问题的可能性（我的意图是将同一个乘法与一个转置矩阵的副本进行比较，以便进行相同的矩阵乘法，只是顺序改变了。并且还要尝试看看是否存在一个矩阵大小的阈值，在该阈值以下现象是不可见的，这也将验证缓存问题，因为要使其成为问题，整个矩阵不能适应缓存）

但是，在这样做的同时，第一步也是开始避免偏差，因为第一个计算使用尚未在缓存中的数据，而第二个使用已经在缓存中的数据（特别是当整个矩阵适应缓存的情况下）。

所以，这是我尝试的第一件事：只是倒置计算顺序。先在转置矩阵上进行计算，然后再在矩阵上进行计算。

这次，转变有利于蓝点（当然，我只改变了计算顺序，而没有改变轴的含义。所以x仍然是矩阵@矩阵的计时，y仍然是转置矩阵）。

这次红点的数量是318对682。所以，几乎完全与之前相反。

因此，结论（至少对我的机器有效）：这确实是一个缓存问题。但这个缓存问题只是由于对转置矩阵有偏见导致的：当你用它来计算时，它已经在缓存中（因为数据与矩阵的数据相同）。

编辑：关于问题更新。

正如我在评论中所说（但由于问题已经更新，而且这个答案已经得到了相当多的赞同，我认为它也应该出现在那个答案中，供未来读者参考），更新是另一回事。

你的第一个问题是关于 A@A 和 A.T@A.T 的比较。第二个似乎更快。但这只是因为有一个单独的操作。所以，如我所示，原因只是因为在执行第二个操作时，A 已经在缓存内存中（而第一个操作时不是这样的）。因为 A.T 是与 A 相同的数据（不是副本。而是相同的数据，在相同的内存地址）。

我之前的回答表明，如果你反过来计算 A.T@A.T，然后是 A@A，那么相反地，A.T@A.T 就会更慢，按照完全相同的比例。

另一种展示的方式是

import numpy as np
import timeit 

A=np.random.normal(0,1,(1000,1000))
B=A.copy()

A@A
print(timeit.timeit(lambda: A@A, number=20))
A.T@A.T
print(timeit.timeit(lambda: A.T@A.T, number=20))
B@B
print(timeit.timeit(lambda: B@B, number=20))

（在使用timeit之前执行A@A的事实只是为了确保由于缓存考虑而导致的前20次计算不会变慢）

在我的电脑上，所有这些操作几乎都需要1秒钟（选择number=20是为了使其花费1秒钟）

这次没有缓存效应，因为我们每个运行都运行了21次，不计算第一次运行的时间。并且.T没有影响

现在，对于您的问题更新，那是另外一回事

A@A.T
print(timeit.timeit(lambda: A@A.T, number=20))
A.T@A
print(timeit.timeit(lambda: A.T@A, number=20))
A@B.T
print(timeit.timeit(lambda: A@B.T, number=20))

这次，前两个操作只需要650毫秒。并不是因为缓存的原因：无论这些操作的顺序如何，时间都是一样的。

这是因为NumPy能够检测到A.T和A是同一个矩阵，只是进行了一次转置操作。 （对于它来说很容易检测到这一点：数据地址相同，但步幅和形状（在这里形状是方阵，但更重要的是，步幅是倒置的）也是倒置的：A.strides → (8000,8)，A.T.strides → (8, 8000)。

因此，NumPy很容易意识到这是一个A@A.T的情况。因此，它会应用一种更快计算的算法。正如评论中所说（以及之前其他人在评论中提到的，但也是几天前其他人误读你的第一个问题时提到的...但他们做得对，因为他们提前回答了现在的更新内容）：A@A.T是对称的。所以，在这里有一些简单的修正。

请注意，

timeit.timeit(lambda: A@B, number=20)
timeit.timeit(lambda: A@B.T, number=20)

都是1秒钟（如A@A和A.T@A.T）。所以，很容易理解A@B、A@A、A.T@A.T都只使用了一个标准的“矩阵乘法”算法。而A@A.T、A.T@A则使用了更快的算法。

由于B是A的副本，A@B.T的结果与A@A.T相同对称。但这一次，因为它是一个副本，numpy无法意识到它是一个A@A.T的情况，无法意识到它是一个对称结果（在计算结果之前）。所以A@B.T的计时与A@A一样标准的“1秒”。而A@A.T则不是。

这证实了它确实依赖于“相同地址，反转步长”准则。只要不是相同的地址或者不是相同的反转步长，标准算法需要1秒钟。如果既是相同的地址又是反转步长，那么特殊算法只需要650毫秒。

- chrslg