点到椭圆的距离

Question

我需要计算点与椭圆之间的距离。在我的程序中，我将椭圆描述为坐标x = acosφ和y = bsinφ（其中a、b是常数，φ是变化的角度）。

我想计算点P与我的椭圆之间的最短距离。我的想法是计算从椭圆中心到点P的向量，然后找到从中心开始并朝向点P并在椭圆末端到达的向量，并在末端减去两个向量以得到距离（这可能不会给出最短距离，但对于我所需的情况仍然可以）。问题是我不知道如何计算第二个向量。有人有更好的想法或可以告诉我如何找到第二个向量吗？

提前谢谢！

---

编辑1:

问题:计算的角度似乎不能给出正确的椭圆上的点

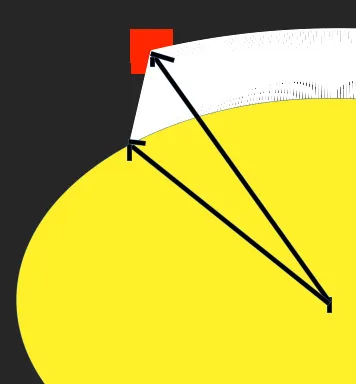
根据的建议，我得到了这个结果:

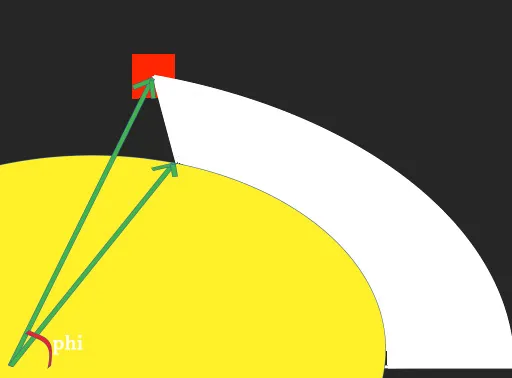
白色部分是由计算距离的程序创建的。我使用从椭圆中心P到身体中心的向量计算角度phi。但是，由于我在椭圆的方程中使用角度来获取应该停留在椭圆上且具有与第一个计算向量相同方向的点（如果我们将该点视为向量），因此实际上会得到上面显示的“延迟”向量。可能出了什么问题？我真的无法理解这种行为（是否与atan2有关）。

编辑2：我还展示了椭圆的另一半给出了这个结果：

所以我们可以看到，这只有在phi = -+pi/2和phi = -+pi的情况下才有效。

---

实现失败

我尝试使用 MARTIN R 的实现，但我仍然做错了事情。

起初我以为可能是中心点（不总是相同的）的问题，于是我这样改变了实现方式：

func pointOnEllipse(ellipse: Ellipse, p: CGPoint) -> CGPoint {

    let maxIterations = 10
    let eps = CGFloat(0.1/max(ellipse.a, ellipse.b))

    // Intersection of straight line from origin to p with ellipse
    // as the first approximation:
    var phi = atan2(ellipse.a*p.y, ellipse.b*p.x)

    // Newton iteration to find solution of
    // f(θ) := (a^2 − b^2) cos(phi) sin(phi) − x a sin(phi) + y b cos(phi) = 0:
    for _ in 0..<maxIterations {
        // function value and derivative at phi:
        let (c, s) = (cos(phi), sin(phi))
        let f = (ellipse.a*ellipse.a - ellipse.b*ellipse.b)*c*s - p.x*ellipse.a*s + p.y*ellipse.b*c - ellipse.center.x*ellipse.a*s + ellipse.center.y*ellipse.b*c
        //for the second derivative
        let f1 = (ellipse.a*ellipse.a - ellipse.b*ellipse.b)*(c*c - s*s) - p.x*ellipse.a*c - p.y*ellipse.b*s - ellipse.center.x*ellipse.a*c - ellipse.center.y*ellipse.b*s

        let delta = f/f1
        phi = phi - delta
        if abs(delta) < eps { break }
    }

  return CGPoint(x: (ellipse.a * cos(phi)) + ellipse.center.x, y: (ellipse.b * sin(phi)) + ellipse.center.y)

}

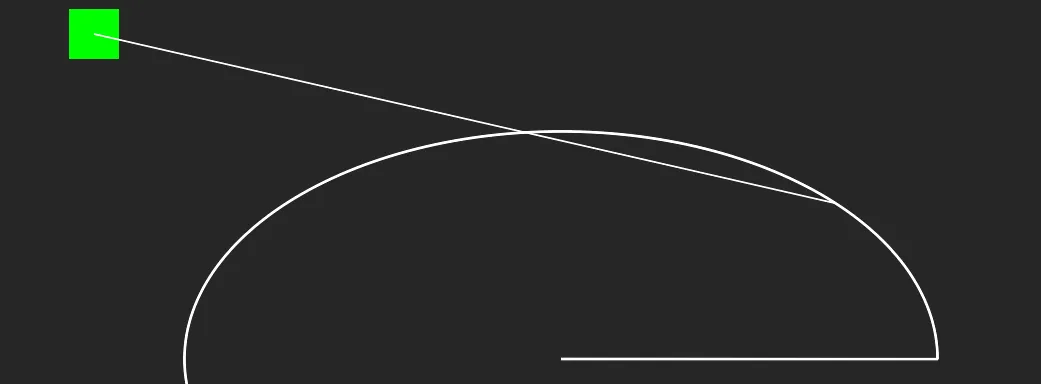
我们可以看到这里发生了什么：

这很奇怪，所有点都停留在那个“象限”里。但我还注意到，当我将绿框远离椭圆时，它似乎会得到正确的距离向量。

可能是什么原因呢？

---

最终结果

使用更新版本的 MARTIN R（进行了3次迭代）

- DevX10

---

你看到这个网址了吗？https://dev59.com/y2Ag5IYBdhLWcg3w9fDm - Sulthan

Answer 1

x = a cos(phi), y = b sin (phi) 是以原点为中心的椭圆形状。根据你提出的问题，可以通过以下方式实现：

// Point on ellipse in the direction of `p`:
let phi = atan2(a*p.y, b*p.x)
let p2 = CGPoint(x: a * cos(phi), y: b * sin(phi))

// Vector from `p2` to `p`:
let v = CGVector(dx: p.x - p2.x, dy: p.y - p2.y)

// Length of `v`:
let distance = hypot(v.dx, v.dy)

您说得对，这并不给出点到椭圆的最短距离。这需要解决四次多项式方程，例如请参见distance from given point to given ellipse或Calculating Distance of a Point from an Ellipse Border。

下面是一种可能的算法实现，该算法在http://wwwf.imperial.ac.uk/~rn/distance2ellipse.pdf中有描述：

// From http://wwwf.imperial.ac.uk/~rn/distance2ellipse.pdf .

func pointOnEllipse(center: CGPoint, a: CGFloat, b: CGFloat, closestTo p: CGPoint) -> CGPoint {

    let maxIterations = 10
    let eps = CGFloat(0.1/max(a, b))

    let p1 = CGPoint(x: p.x - center.x, y: p.y - center.y)

    // Intersection of straight line from origin to p with ellipse
    // as the first approximation:
    var phi = atan2(a * p1.y, b * p1.x)

    // Newton iteration to find solution of
    // f(θ) := (a^2 − b^2) cos(phi) sin(phi) − x a sin(phi) + y b cos(phi) = 0:
    for i in 0..<maxIterations {
        // function value and derivative at phi:
        let (c, s) = (cos(phi), sin(phi))
        let f = (a*a - b*b)*c*s - p1.x*a*s + p1.y*b*c
        let f1 = (a*a - b*b)*(c*c - s*s) - p1.x*a*c - p1.y*b*s

        let delta = f/f1
        phi = phi - delta
        print(i)
        if abs(delta) < eps { break }
    }

    return CGPoint(x: center.x + a * cos(phi), y: center.y + b * sin(phi))
}

您可能需要根据自己的需求调整最大迭代次数和epsilon，但是这些值对我而言效果很好。对于椭圆外的点，最多需要3次迭代才能找到解的良好近似值。

使用此方法，您可以计算距离

let p2 = pointOnEllipse(a: a, b: b, closestTo: p)
let v = CGVector(dx: p.x - p2.x, dy: p.y - p2.y)
let distance = hypot(v.dx, v.dy)

- Martin R

---

我简直不敢相信，我尝试了所有的方法，包括一个与你的计算类似的方法，但它显然是如此明显...谢谢，我现在会尝试一下并告诉你是否有效 :) - DevX10

正如我所想，这并不容易。我非常确定这对于一个圆来说是完美的，但在这种情况下，角度“phi”实际上并没有给出我需要的点。这是因为没有固定的半径，而是两个不同的半径。 - DevX10

我认为这是因为没有固定的半径，而是两个常数改变了这个东西。我会在我的编辑问题中展示发生了什么。 - DevX10

感谢这个更新，我已经尝试并更新了我的问题。 - DevX10

@Ergo：在你的代码中，椭圆中心不是原点的情况没有被正确处理。请参考更新后的答案。 - Martin R

所以你只需使用相同的问题，但将点P相对于椭圆的中心（点P1）表示。太棒了，它最终开始工作了。非常感谢。 - DevX10

Answer 2

我使用Latex写了一篇说明，以使其更易读，并拍摄了一些屏幕截图。我分享的方法是使用基于牛顿步骤的优化方法来解决问题。

请注意，对于长短轴长度比较小的椭圆情况，您只需要进行几次迭代即可获得相当好的精度。对于更小的比率，甚至可以仅使用初始猜测结果，这基本上就是Martin R所展示的内容。但如果您的椭圆可以是任何形状，您可能需要添加一些代码来改善近似值。

- spektr

---

这真的很有趣，我想我会尝试一下。它看起来非常不错，但是如果我使用的椭圆的比例几乎永远都不大于4（考虑a / b），你会建议我做什么呢？您仍然建议我使用牛顿迭代或采用更简单、计算量更小的方法吗？ - DevX10

根据上述算法，我建议进行1或2次牛顿迭代，具体取决于您想要的精度水平。如果您可以接受一些误差，则不使用任何牛顿步骤也可以。我还注意到Martin R更新了他的答案，并提供了一些Swift代码来执行牛顿迭代细化，因此看起来您不需要过多担心实现问题。 - spektr

Answer 3

创建新的坐标系，将椭圆通过https://math.stackexchange.com/questions/79842/is-an-ellipse-a-circle-transformed-by-a-simple-formula简单公式转换为圆形，然后找到点到圆的距离，并将距离转换。

- Alex Aparin

---

很有趣，你能更好地解释一下你会怎么做吗？ - DevX10

@DevX10 这绝对是最简单的解决方案；已经确认在 HTML5 画布上可以使用（我的用例）。链接的问题/答案很重要：它表明椭圆确实“只是”一个圆加上坐标系的仿射变换。你不需要计算到椭圆的距离，而是将问题简化为计算到圆的距离。你需要转换矩阵，将圆形转换为你的椭圆（在 HTML5 画布的情况下，它会在你平移和倾斜以从圆形得到椭圆后给出）。然后获取逆矩阵变换...（待续） - rawpower

...然后将计算距离的点转换为圆的坐标系，然后计算距离。最后，使用将圆转换为椭圆的相同变换将距离转换为您的正常坐标系。您可以自由选择圆，半径不重要，只要它可以转换为椭圆即可。我选择椭圆的两个“半径”中较小的一个作为圆的半径。一切都运行良好且快速，只需进行几次矩阵乘法（由Canvas代替我执行）。 - rawpower

最后，矩阵的反转并不复杂，但大多数图形系统 - 包括HTML5 Canvas - 可能会为您完成它，因此您也不必担心。严谨地说：由HTML5 Canvas返回的DOMMatrix早于Canvas本身，并且可以独立使用。 - rawpower

Answer 4

你有一个椭圆中心 (a, b) 和任意一点 P(Px, Py)。由这两个点定义的直线方程如下：

(Y - Py) / (b - Py) = (X - Px) / (a - Px)

另一个形式是一个椭圆。你需要找出哪些 (X, Y) 点既在椭圆上，又在中心和该点之间的直线上。会有两个这样的点，你需要计算它们到 P 的距离并选择较小的距离。

- Lajos Arpad