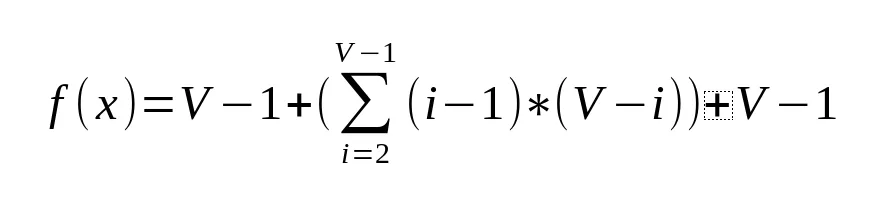最近，我了解了最短路径快速算法。我想知道如何构建一个测试案例来使标准的SPFA实现非常非常慢。你知道吗？
通过标准实现，我是指维基百科上的这个：
procedure Shortest-Path-Faster-Algorithm(G, s)
1 for each vertex v ≠ s in V(G)
2 d(v) := ∞
3 d(s) := 0
4 offer s into Q
5 while Q is not empty
6 u := poll Q
7 for each edge (u, v) in E(G)
8 if d(u) + w(u, v) < d(v) then
9 d(v) := d(u) + w(u, v)
10 if v is not in Q then
11 offer v into Q
在每次迭代中，队列将会有以下元素（队列头为最左边的元素）：[1]
[5, 4, 3, 2]
[4, 3, 2]
[3, 2]
[2]
[5, 4, 3]
[4, 3]
[3]
[5, 4]
[4]
[5]
| 顶点 | 取出次数 | 出边数 | if语句执行次数 |
|---|---|---|---|
| 1 | 1 | 4 | 4 |
| 2 | 1 | 3 | 3 |
| 3 | 2 | 2 | 4 |
| 4 | 3 | 1 | 3 |
| 5 | 4 | 0 | 4 |
我尝试使用实际代码测试了所有之前的答案，除了Luis的答案外，其他答案似乎都不正确。（SPFA在Ke和Vit的答案上都以$O(N)$时间运行）。
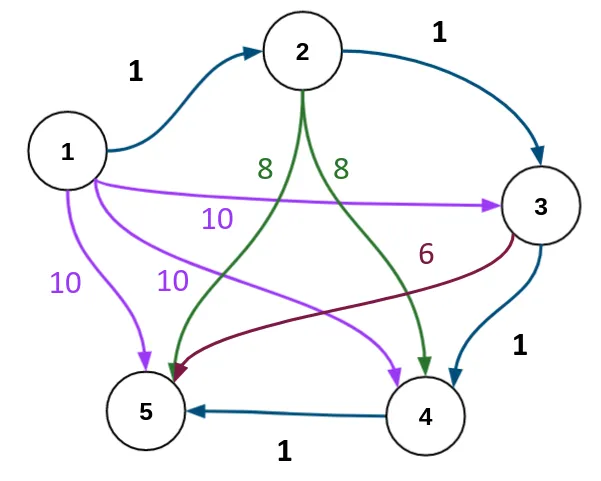
请注意，Luis的构造产生了一个密集图。为了完整起见，这里提供了一个额外的测试用例，其中涉及具有非负权重的$O(N)$边，其中SPFA在$\Theta(N^2)$时间内运行。构造如下：
顶点$N/2$被推入队列$\Theta(N)$次，每次我们从队列中弹出它时，需要花费$\Theta(N)$的时间来迭代其邻接列表，从而得到所需的复杂度。
C++源代码：
#include <cassert>
#include <climits>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
ostream &operator<<(ostream &os, pair<int, int> p) {
os << "{" << p.first << ", " << p.second << "}";
return os;
}
template <class T> ostream &operator<<(ostream &os, const vector<T> &v) {
os << "{";
for (size_t i = 0; i < size(v); ++i) {
if (i) os << ", ";
os << v[i];
}
os << "}";
return os;
}
struct Edge {
int u, v, w;
};
vector<int> spfa(int N, vector<Edge> edges) {
vector<vector<pair<int, int>>> adj(N);
for (auto [u, v, w] : edges) {
assert(0 <= u && u < N);
assert(0 <= v && v < N);
adj[u].push_back({v, w});
}
cerr << "Input:\n";
for (int i = 0; i < N; ++i) {
cerr << "adj[" << i << "] = ";
cerr << adj[i] << "\n";
}
cerr << "\n";
vector<int> d(N, INT_MAX);
d[0] = 0;
queue<int> q;
vector<bool> in_queue(N);
int ops = 0;
cerr << "Ops:\n";
auto offer = [&](int v) {
if (in_queue.at(v)) return;
cerr << "offer "
<< "v = " << v << " "
<< "d[v] = " << d[v] << "\n";
// cerr << "offer " << v << " " << d << "\n";
in_queue.at(v) = true;
q.push(v);
};
auto poll = [&]() {
int u = q.front();
q.pop();
assert(in_queue.at(u));
in_queue.at(u) = false;
return u;
};
offer(0);
while (!q.empty()) {
int u = poll();
cerr << "poll "
<< "u = " << u << " "
<< "d[u] = " << d[u] << "\n";
// cerr << "poll " << u << " " << d << "\n";
for (auto [v, w] : adj[u]) {
++ops;
int new_d = d[u] + w;
if (new_d < d[v]) d[v] = new_d, offer(v);
}
}
cerr << "ops = " << ops << "\n";
return d;
}
// Ke Yang's case (0-indexed)
// ops ~ 3*N
vector<Edge> gen_ke(int N) {
vector<Edge> edges;
for (int i = N - 1; i > 0; --i) edges.push_back({0, i, 2 * N});
for (int i = 0; i < N - 1; ++i) edges.push_back({i, i + 1, 1});
return edges;
}
// ops ~ 3*N
vector<Edge> gen_vit(int N) {
vector<Edge> edges;
for (int i = N - 1; i > 0; --i) edges.push_back({0, i, 3 * N - 2 * i});
for (int i = 0; i < N - 1; ++i) edges.push_back({i, i + 1, 1});
return edges;
}
// O(N^2) edges, ops ~ N^3 / 6
vector<Edge> gen_luis(int N) {
vector<Edge> edges;
for (int i = 0; i < N; ++i)
for (int j = i + 2; j < N; ++j) edges.push_back({i, j, 2 * (N - i)});
for (int i = 0; i + 1 < N; ++i) edges.push_back({i, i + 1, 1});
return edges;
}
// O(N) edges, ops ~ N^2/4
vector<Edge> gen_good(int N) {
vector<Edge> edges;
for (int i = 0; i < N / 2; ++i) edges.push_back({i, N / 2, N - i});
for (int i = N / 2 + 1; i < N; ++i) edges.push_back({N / 2, i, 0});
for (int i = 0; i < N / 2 - 1; ++i) edges.push_back({i, i + 1, 0});
return edges;
}
int main() {
int N = 100;
// auto edges = gen_ke(N);
// auto edges = gen_vit(N);
// auto edges = gen_luis(N);
auto edges = gen_good(N);
vector<int> dists = spfa(N, edges);
cout << dists << "\n";
}
在Ke Yang的测试用例中，当$N=10$时的输出：
Input:
adj[0] = {{9, 20}, {8, 20}, {7, 20}, {6, 20}, {5, 20}, {4, 20}, {3, 20}, {2, 20}, {1, 20}, {1, 1}}
adj[1] = {{2, 1}}
adj[2] = {{3, 1}}
adj[3] = {{4, 1}}
adj[4] = {{5, 1}}
adj[5] = {{6, 1}}
adj[6] = {{7, 1}}
adj[7] = {{8, 1}}
adj[8] = {{9, 1}}
adj[9] = {}
Ops:
offer v = 0 d[v] = 0
poll u = 0 d[u] = 0
offer v = 9 d[v] = 20
offer v = 8 d[v] = 20
offer v = 7 d[v] = 20
offer v = 6 d[v] = 20
offer v = 5 d[v] = 20
offer v = 4 d[v] = 20
offer v = 3 d[v] = 20
offer v = 2 d[v] = 20
offer v = 1 d[v] = 20
poll u = 9 d[u] = 20
poll u = 8 d[u] = 20
poll u = 7 d[u] = 20
poll u = 6 d[u] = 20
poll u = 5 d[u] = 20
poll u = 4 d[u] = 20
poll u = 3 d[u] = 20
poll u = 2 d[u] = 20
poll u = 1 d[u] = 1
offer v = 2 d[v] = 2
poll u = 2 d[u] = 2
offer v = 3 d[v] = 3
poll u = 3 d[u] = 3
offer v = 4 d[v] = 4
poll u = 4 d[u] = 4
offer v = 5 d[v] = 5
poll u = 5 d[u] = 5
offer v = 6 d[v] = 6
poll u = 6 d[u] = 6
offer v = 7 d[v] = 7
poll u = 7 d[u] = 7
offer v = 8 d[v] = 8
poll u = 8 d[u] = 8
offer v = 9 d[v] = 9
poll u = 9 d[u] = 9
ops = 25
通过对边缘进行随机洗牌，可以轻松破解Ke Yang的测试。
进行小修改即可防止这种情况发生：边缘必须是(i, i+1, 1)和(1, i, N*3-i*2)。