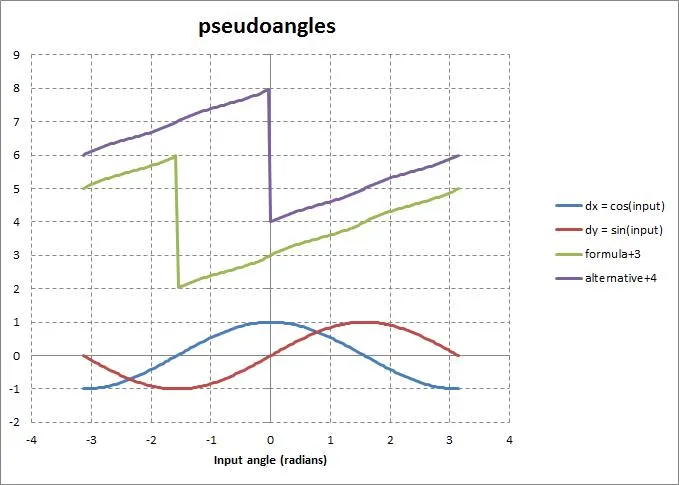
atan2调用可能是浪费的。有什么更快的方法来计算严格单调的角度值,就像atan2一样?这样的函数显然被一些人称为“伪角”。atan2调用可能是浪费的。有什么更快的方法来计算严格单调的角度值,就像atan2一样?这样的函数显然被一些人称为“伪角”。我开始试着操作这个函数,发现其规范有点不完整。由于dx和dy变化时,atan2会在某一点上在-pi和+pi之间跳跃,从而导致不连续性。下面的图表显示了@MvG建议的两个公式,实际上它们与atan2相比,在不同的位置都存在不连续性。(注:我在第一个公式中添加了3,在备选项中添加了4,以使线在图上不重叠)。如果将atan2添加到该图中,则它将是y = x的直线。因此,我认为可能会有各种答案,具体取决于人们想要放置不连续性的位置。如果真的想复制atan2,那么答案(在这个类别中)将是
# Input: dx, dy: coordinates of a (difference) vector.
# Output: a number from the range [-2 .. 2] which is monotonic
# in the angle this vector makes against the x axis.
# and with the same discontinuity as atan2
def pseudoangle(dx, dy):
p = dx/(abs(dx)+abs(dy)) # -1 .. 1 increasing with x
if dy < 0: return p - 1 # -2 .. 0 increasing with x
else: return 1 - p # 0 .. 2 decreasing with x
pseudoangle = copysign(1. - dx/(fabs(dx)+fabs(dy)),dy)
@MvG说这个很好用,我也觉得看起来不错 :-).
copysign(1.-x/(fabs(x)+fabs(y)),y),相比于atan2,我观察到至少快了10倍,这与@george的观察相反,他认为这可能比atan2更慢。如果您认为合适,可以随意将这个C代码片段包含在您的答案中。 - MvG# Input: dx, dy: coordinates of a (difference) vector.
# Output: a number from the range [-1 .. 3] (or [0 .. 4] with the comment enabled)
# which is monotonic in the angle this vector makes against the x axis.
def pseudoangle(dx, dy):
ax = abs(dx)
ay = abs(dy)
p = dy/(ax+ay)
if dx < 0: p = 2 - p
# elif dy < 0: p = 4 + p
return p
我不知道上述函数是否有一个已经确定的名称,以及谁最先发布了它。我很久以前就得到了它,并从一个项目复制到另一个项目。然而,我在网上找到了这个函数的多个实例,因此我认为这个片段足够公开,可以被重用。
有一种方法可以获得范围[0 … 4](对于实际角度[0 … 2π]),而不引入进一步的情况区分:
# Input: dx, dy: coordinates of a (difference) vector.
# Output: a number from the range [0 .. 4] which is monotonic
# in the angle this vector makes against the x axis.
def pseudoangle(dx, dy):
p = dx/(abs(dx)+abs(dy)) # -1 .. 1 increasing with x
if dy < 0: return 3 + p # 2 .. 4 increasing with x
else: return 1 - p # 0 .. 2 decreasing with x
double pseudoangle(double dx, double dy)
{
// 1 for above, 0 for below the diagonal/anti-diagonal
int diag = dx > dy;
int adiag = dx > -dy;
double r = !adiag ? 4 : 0;
if (dy == 0)
return r;
if (diag ^ adiag)
r += 2 - dx / dy;
else
r += dy / dx;
return r;
}
pseudoangle(dx,dy) + 1 % 8 == Fowler(dx,dy)
谈到性能,它比Fowler的代码少得多(在我看来通常也不太复杂)。在gcc 6.1.1上使用-O3编译,上述函数生成带有4个分支的汇编代码,其中两个来自dy == 0(一个检查是否两个操作数都是“无序”的,因此如果dy是NaN,另一个则检查它们是否相等)。看一下分支的来源,我们可以得出以下观察:
我的代码不依赖于abs或copysign,这使它看起来更加自包含。然而,在浮点值上处理符号位实际上相当简单,因为它只是翻转一个单独的位(没有分支!),所以这更像是一个劣势。
此外,其他在此处提出的解决方案在除以abs(dx) + abs(dy)之前并不检查它是否等于0,但是只要一个分量(dy)为0,这个版本就会失败——因此引入了一个分支(或者在我的情况下是两个分支)。
如果我们选择获得大致相同的结果(最多存在舍入误差),但没有分支,我们可以滥用copysign并编写:
double pseudoangle(double dx, double dy)
{
double s = dx + dy;
double d = dx - dy;
double r = 2 * (1.0 - copysign(1.0, s));
double xor_sign = copysign(1.0, d) * copysign(1.0, s);
r += (1.0 - xor_sign);
r += (s - xor_sign * d) / (d + xor_sign * s);
return r;
}
signed int compare(double x1, double y1, double x2, double y2) {
unsigned int d1 = x1 > y1;
unsigned int d2 = x2 > y2;
unsigned int a1 = x1 > -y1;
unsigned int a2 = x2 > -y2;
// Quotients of both angles.
unsigned int qa = d1 * 2 + a1;
unsigned int qb = d2 * 2 + a2;
if(qa != qb) return((0x6c >> qa * 2 & 6) - (0x6c >> qb * 2 & 6));
d1 ^= a1;
double p = x1 * y2;
double q = x2 * y1;
// Numerator of each remainder, multiplied by denominator of the other.
double na = q * (1 - d1) - p * d1;
double nb = p * (1 - d1) - q * d1;
// Return signum(na - nb)
return((na > nb) - (na < nb));
}
divss而花费更多指令通常是不值得的;FP除法仍然只有1个uop,并且具有足够好的吞吐量,不会成为主要瓶颈。它的延迟较差,如果你可以便宜地避免它(例如,在循环中乘以倒数),那么就值得避免。浮点除法与浮点乘法 - Peter Cordesusing StableRNGs
using BenchmarkTools
# Definitions
struct V{T}
x::T
y::T
end
function pseudoangle(v)
copysign(1. - v.x/(abs(v.x)+abs(v.y)), v.y)
end
function isangleless(v1, v2)
a1 = abs(v1.x) + abs(v1.y)
a2 = abs(v2.x) + abs(v2.y)
a2*copysign(a1 - v1.x, v1.y) < a1*copysign(a2 - v2.x, v2.y)
end
# Data
rng = StableRNG(2021)
vectors = map(x -> V(x...), zip(rand(rng, 1000), rand(rng, 1000)))
# Comparison
res1 = sort(vectors, by = x -> pseudoangle(x));
res2 = sort(vectors, lt = (x, y) -> isangleless(x, y));
@assert res1 == res2
@btime sort($vectors, by = x -> pseudoangle(x));
# 110.437 μs (3 allocations: 23.70 KiB)
@btime sort($vectors, lt = (x, y) -> isangleless(x, y));
# 65.703 μs (3 allocations: 23.70 KiB)
因此,避免使用除法,可以将时间减少一半而不会降低结果质量。当然,对于更精确的计算,isangleless 有时需要配备 bigfloat,但同样也适用于 pseudoangle。
def pseudoangle( dy , dx ):
""" returns approximation to math.atan2(dy,dx)*2/pi"""
if dx == 0 :
s = cmp(dy,0)
else::
s = cmp(dx*dy,0) # cmp == "sign" in many other languages.
if s == 0 : return 0 # doesnt hurt performance much.but can omit if 0,0 never happens
p = dy/(dx+s*dy)
if dx < 0: return p-2*s
return p
atan2 是一个单一的本地函数调用,但伪角实现需要进行多个解释算术运算,可能需要类型检查,因此使用伪角确实可能对性能不利。 - MvG只需使用叉积函数。您旋转一个线段相对于另一个的方向将给出正数或负数。没有三角函数,也没有除法。快速简单。只需谷歌一下。