我几周前在Google+上看到一条评论，其中有人展示了一种简单的斐波那契数列计算方法，它不基于递归，也没有使用记忆化。他只需记住最后两个数字并将它们相加。这是一个O(n)算法，但他实现得非常干净。所以我很快指出更快的方法是利用它们可以作为[[0,1]，[1,1]]矩阵的幂次来计算，这只需要进行O(log(N))计算。
当然，问题在于这远非在某一点过后的最优解。只要数字不太大，它就是有效的，但它们的长度以N*log(phi)/log(10)的速率增长，其中N是第N个斐波那契数，phi是黄金比例((1+sqrt(5))/2约为1.6)。事实证明，log(phi)/log(10)非常接近1/5。因此，第N个斐波那契数可以预计具有大约N/5位数。
矩阵乘法，甚至数字相乘，当数字开始变成数百万或数十亿位时，速度会变得非常慢。因此，在Python中计算F（100,000）大约需要0.03秒，而计算F（1000,000）则需要大约5秒。这几乎不是O（log（N））增长。我的估计是，即使没有改进，该方法也仅将计算优化为O（（log（N））^（2.5））左右。
以这种速度计算十亿级的斐波那契数列，将会非常缓慢（即使它只有约1,000,000,000/5位数字，因此轻松适合32位内存）。
是否有人知道一种实现或算法，可以允许更快的计算？也许有些东西可以计算万亿级的斐波那契数。
只是为了明确，我不是在寻找近似值。我正在寻找精确计算（到最后一位）。
编辑1：我正在添加Python代码，以显示我认为是O（（log N）^ 2.5）算法。
我希望不需要计算元素（0,0）会使速度提高额外的1 /（1 + phi + phi * phi）〜19％。但是由Eli Korvigo提供的F（2N）和F（2N-1）的
当然，问题在于这远非在某一点过后的最优解。只要数字不太大，它就是有效的，但它们的长度以N*log(phi)/log(10)的速率增长，其中N是第N个斐波那契数，phi是黄金比例((1+sqrt(5))/2约为1.6)。事实证明，log(phi)/log(10)非常接近1/5。因此，第N个斐波那契数可以预计具有大约N/5位数。
矩阵乘法，甚至数字相乘，当数字开始变成数百万或数十亿位时，速度会变得非常慢。因此，在Python中计算F（100,000）大约需要0.03秒，而计算F（1000,000）则需要大约5秒。这几乎不是O（log（N））增长。我的估计是，即使没有改进，该方法也仅将计算优化为O（（log（N））^（2.5））左右。
以这种速度计算十亿级的斐波那契数列，将会非常缓慢（即使它只有约1,000,000,000/5位数字，因此轻松适合32位内存）。
是否有人知道一种实现或算法，可以允许更快的计算？也许有些东西可以计算万亿级的斐波那契数。
只是为了明确，我不是在寻找近似值。我正在寻找精确计算（到最后一位）。
编辑1：我正在添加Python代码，以显示我认为是O（（log N）^ 2.5）算法。
from operator import mul as mul
from time import clock
class TwoByTwoMatrix:
__slots__ = "rows"
def __init__(self, m):
self.rows = m
def __imul__(self, other):
self.rows = [[sum(map(mul, my_row, oth_col)) for oth_col in zip(*other.rows)] for my_row in self.rows]
return self
def intpow(self, i):
i = int(i)
result = TwoByTwoMatrix([[long(1),long(0)],[long(0),long(1)]])
if i <= 0:
return result
k = 0
while i % 2 == 0:
k +=1
i >>= 1
multiplier = TwoByTwoMatrix(self.rows)
while i > 0:
if i & 1:
result *= multiplier
multiplier *= multiplier # square it
i >>= 1
for j in xrange(k):
result *= result
return result
m = TwoByTwoMatrix([[0,1],[1,1]])
t1 = clock()
print len(str(m.intpow(100000).rows[1][1]))
t2 = clock()
print t2 - t1
t1 = clock()
print len(str(m.intpow(1000000).rows[1][1]))
t2 = clock()
print t2 - t1
编辑2：
看来我没有考虑到len(str(...))会对测试的总运行时间产生显著的贡献。将测试更改为
from math import log as log
t1 = clock()
print log(m.intpow(100000).rows[1][1])/log(10)
t2 = clock()
print t2 - t1
t1 = clock()
print log(m.intpow(1000000).rows[1][1])/log(10)
t2 = clock()
print t2 - t1
缩短了运行时间为0.008秒和0.31秒（从使用len(str(...))时的0.03秒和5秒）。
因为M = [[0,1]，[1,1]]的N次方等于[[F(N-2), F(N-1)]，[F(N-1), F(N)]]， 另一个明显的低效率来源是将矩阵的(0,1)和(1,0)元素计算为不同的元素。这样做的效率较低（我已经切换到Python3，但Python2.7的时间类似）：
class SymTwoByTwoMatrix():
# elments (0,0), (0,1), (1,1) of a symmetric 2x2 matrix are a, b, c.
# b is also the (1,0) element because the matrix is symmetric
def __init__(self, a, b, c):
self.a = a
self.b = b
self.c = c
def __imul__(self, other):
# this multiplication does work correctly because we
# are multiplying powers of the same symmetric matrix
self.a, self.b, self.c = \
self.a * other.a + self.b * other.b, \
self.a * other.b + self.b * other.c, \
self.b * other.b + self.c * other.c
return self
def intpow(self, i):
i = int(i)
result = SymTwoByTwoMatrix(1, 0, 1)
if i <= 0:
return result
k = 0
while i % 2 == 0:
k +=1
i >>= 1
multiplier = SymTwoByTwoMatrix(self.a, self.b, self.c)
while i > 0:
if i & 1:
result *= multiplier
multiplier *= multiplier # square it
i >>= 1
for j in range(k):
result *= result
return result
在0.006秒内计算出F(100,000)，在0.235秒内计算出F(1,000,000)，在9.51秒内计算出F(10,000,000)，这是可以预期的。最快测试结果比预期快45％，预计增益应该渐近地接近phi /（1 + 2 * phi + phi * phi）〜23.6％。
M ^ N的（0,0）元素实际上是第N-2个斐波那契数：
for i in range(15):
x = m.intpow(i)
print([x.a,x.b,x.c])
提供
[1, 0, 1]
[0, 1, 1]
[1, 1, 2]
[1, 2, 3]
[2, 3, 5]
[3, 5, 8]
[5, 8, 13]
[8, 13, 21]
[13, 21, 34]
[21, 34, 55]
[34, 55, 89]
[55, 89, 144]
[89, 144, 233]
[144, 233, 377]
[233, 377, 610]
我希望不需要计算元素（0,0）会使速度提高额外的1 /（1 + phi + phi * phi）〜19％。但是由Eli Korvigo提供的F（2N）和F（2N-1）的
lru_cache solution given by Eli Korvigo below实际上加速了4倍（即75％）。因此，虽然我没有找到正式的解释，但我倾向于认为它缓存了N的二进制展开中1的跨度，并执行必要的最小乘法次数。这就避免了查找那些范围，在正确的时刻在N的展开中预先计算它们并将它们相乘。 lru_cache 允许从上到下计算本来会更复杂的自下而上计算。
每次N增长10倍，SymTwoByTwoMatrix和lru_cache-of-F(2N)-and-F(2N-1)的计算时间大致增加了40倍。我认为这可能是由于Python对长整数乘法的实现。我认为大数的乘法和加法应该是可并行化的。因此，即使F(N)的解决方案是Theta(n)（如Daniel Fisher在评论中所述），也应该可以实现一个多线程的子O(N)解决方案。
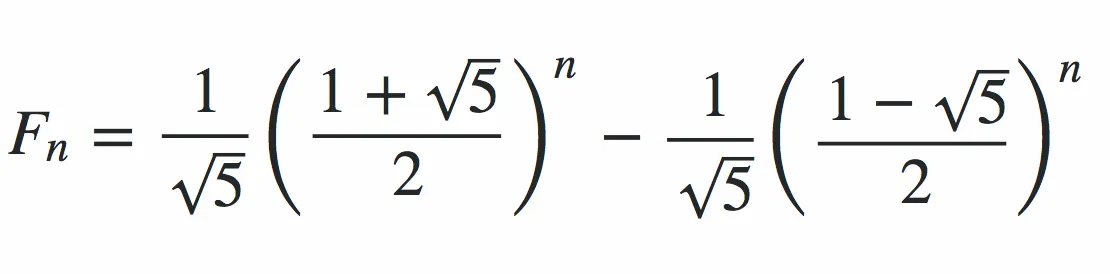
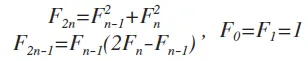
F(n)有Theta(n)位（无论在哪个基础上的数字），因此您 无法 比O(n)更快地计算它。 - Daniel Fischer