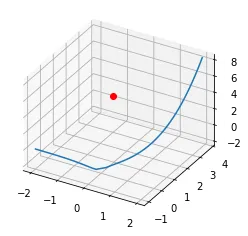
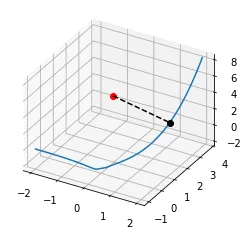
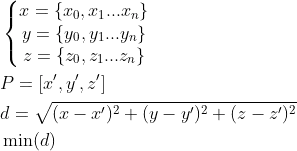我有两个包含三维点(名称、X、Y、Z)的数组。第一个数组包含参考点,通过这些点我正在绘制样条线。第二个数组包含测量点,我需要从中计算法线,并获取法线在样条线上的坐标(我需要计算测量点的XY和高度标准偏差)。这是测试数据(实际上我有几千个点):
1号数组 - 参考点/生成样条线:
r1,1.5602,6.0310,4.8289
r2,1.6453,5.8504,4.8428
r3,1.7172,5.6732,4.8428
r4,1.8018,5.5296,4.8474
r5,1.8700,5.3597,4.8414
第二个数组 - 测量点:
m1, 1.8592, 5.4707, 4.8212
m2, 1.7642, 5.6362, 4.8441
m3, 1.6842, 5.7920, 4.8424
m4, 1.6048, 5.9707, 4.8465
我所编写的代码,用于读取数据,使用scipy计算样条曲线,然后通过matplotlib显示:
import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate
# import measured points
filename = "measpts.csv"
meas_pts = np.genfromtxt(filename, delimiter=',')
# import reference points
filename = "refpts.csv"
ref = np.genfromtxt(filename, delimiter=',')
# divide data to X, Y, Z
x = ref[:, 2]
y = ref[:, 1]
z = ref[:, 3]
# spline interpolation
tck, u = interpolate.splprep([x, y, z], s=0)
u_new = np.linspace(u.min(), u.max(), 1000000)
x_new, y_new, z_new = interpolate.splev(u_new, tck, der=0)
xs = tck[1][0]
ys = tck[1][1]
zs = tck[1][2]
# PLOT 3D
fig = plt.figure()
ax3d = fig.add_subplot(111, projection='3d', proj_type='ortho')
ax3d.plot(x, y, z, 'ro') # ref points
ax3d.plot(xs, ys, zs, 'yo') # spline knots
ax3d.plot(x_new, y_new, z_new, 'b--') # spline
ax3d.plot(meas_pts[:, 2], meas_pts[:, 1], meas_pts[:, 3], 'g*') # measured points
# ax3d.view_init(90, -90) # 2D TOP view
# ax3d.view_init(0, -90) # 2D from SOUTH to NORTH view
# ax3d.view_init(0, 0) # 2D from EAST to WEST view
plt.show()
总结一下:我需要一个包含成对数据的数组:[[测量点 X,Y,Z],[样条曲线上最近(法)点的 X,Y,Z]]。