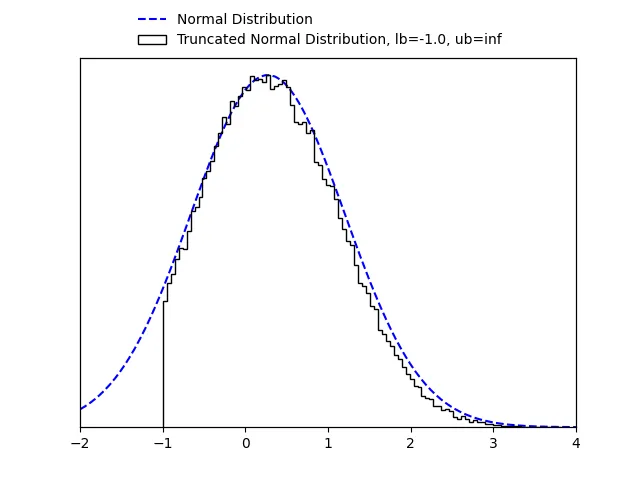
我编写了一个脚本来测量迄今为止提供的解决方案的运行时间。 绘制50维度分布的100个样本时,运行时间如下:
- Botev 2016 implementation 0.029579秒
- Li and Ghosh 2015 implementation 2.597150秒
- 使用emcee 217.914969秒
为比较而言,不使用任何截断的Cholesky分解采样需要0.000201秒。
对于这种特定情况,Botev 2016 implementation 是从截断的多元正态分布中采样的最快方法。 emcee 方法要慢得多,但也许可以调整以提高性能。
该输出是在具有6个内核的x86机器上使用以下代码生成的。
import emcee
from minimax_tilting_sampler import TruncatedMVN
from trun_mvnt import rtmvn
import numpy as np
from scipy import linalg
from multiprocessing import Pool
import time
def log_prob_mvtnd(x, mean, lb, ub, vcm):
if np.any(np.less(x,lb)) or np.any(np.greater(x,ub)):
return -np.inf
else:
diff = x - mean
return -0.5 * np.dot(diff, np.linalg.solve(vcm, diff))
def tmvnd_emcee(vcm,lb,ub,n,mean=None):
ndim = vcm.shape[0]
if not mean:
mean = np.zeros(ndim)
with Pool() as pool:
sampler = emcee.EnsembleSampler(nwalkers=n,
ndim=ndim,
log_prob_fn=log_prob_mvtnd,
args = (mean, lb,ub, vcm),
pool=pool
)
p0 = np.random.multivariate_normal(mean, vcm, size=n)
state = sampler.run_mcmc(p0, 10)
sampler.reset()
sampler.run_mcmc(state, 100);
return sampler.get_last_sample().coords
def mvnd_chol(vcm,n):
gauss_samples = np.random.randn(vcm.shape[0],n)
R = linalg.cholesky(vcm, lower=True)
return np.dot(R,gauss_samples)
def tmvnd_botev16(vcm,lb,ub,n):
tmvn = TruncatedMVN(np.zeros(vcm.shape[0]), vcm, lb, ub)
return tmvn.sample(n)
def tmvnd_Li_Ghosh_15(vcm,lb,ub,n):
burn = 100
thin = 1
D =np.eye((vcm.shape[0]))
return rtmvn(n, np.zeros(vcm.shape[0]), vcm, D, lb, ub, burn, thin).T
if __name__ == '__main__':
ndim=50
nsamples = 100
sigma = np.exp(-1*np.linspace(0, 10, ndim))
vcm = linalg.toeplitz(sigma)
trunc_sigma = 2
ub = np.sqrt(np.diag(vcm))*trunc_sigma
lb = -ub
samplers = { 'not truncated' : lambda vcm,lb,ub,n: mvnd_chol(vcm,n),
'emcee' : lambda vcm,lb,ub,n: tmvnd_emcee(vcm,lb,ub,n),
'Botev 2016': lambda vcm,lb,ub,n: tmvnd_botev16(vcm,lb,ub,n),
'Li and Ghosh 2015': lambda vcm,lb,ub,n: tmvnd_Li_Ghosh_15(vcm,lb,ub,n)}
samples = []
for name, sampler in samplers.items():
start = time.time()
samples.append(sampler(vcm,lb,ub,nsamples))
end = time.time()
print("%s %f s" %(name, end - start))