我正在尝试创建一个类似于这样的形状，由12个五边形组成的六边形，大小任意。
(图片来源)
唯一的问题是，我完全不知道需要什么样的代码来生成它！
目标是能够将3D空间中的一个点转换为网格上的位置坐标，或者反过来，获取网格位置并获得绘制网格所需的相关顶点。
我甚至不知道如何存储此网格的位置。每个三角形区域是否都有自己的2D坐标集？
我最可能会使用C#，但我更感兴趣的是要使用哪些算法以及它们如何工作的解释，而不仅仅是给我一段代码。
数学方法产生球形六边形网格
32
- Aaron Franke
5
1我会从计算12个五边形的位置开始 - 这应该不难。然后，使用球面线性插值（slerp），我会尝试计算每个三角形部分中六边形的位置。这只是我想到的一个想法。 - navyblue
我知道两种方法：1. 半球体的六边形平铺，但这不能用于整个球体，但可以通过旋转时重新映射来伪造。2. 球面三角剖分 如果你从两个六边形开始细分，你就得到了三角形的地图。现在你只需要找到一种将它们映射到你的六边形和五边形的方法。如果你想要更好的球体，可以使用二十面体作为起点。 - Spektre
不确定您打算如何映射网格？即您打算如何为每个网格单元分配一个坐标标签。 - meowgoesthedog
@meowgoesthedog 完全重构，包含新代码和图片。 - Spektre
{btsdaf} - Aaron Franke
3个回答
30
你所拥有的形状是所谓的“Goldberg polyhedra”，也是geodesic polyhedra之一。
生成这个（以及许多其他）的（相当优雅的）算法可以简洁地编码在一个叫做Conway Polyhedron Notation的东西中。
构造步骤很容易跟随，您可以单击下面的图像获取实时预览。
这很容易实现。我建议使用数据结构，使得遍历相邻的顶点、边等变得容易，例如使用有向边或半边数据结构来处理您的网格。您只需要为您要查找的形状实现截取和对偶操作即可。
生成这个（以及许多其他）的（相当优雅的）算法可以简洁地编码在一个叫做Conway Polyhedron Notation的东西中。
构造步骤很容易跟随，您可以单击下面的图像获取实时预览。
你要寻找的多面体可以由一个二十面体生成 -- 用一个二十面体初始化网格。
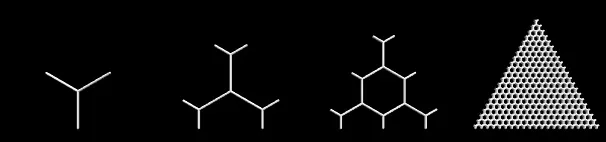
我们对网格应用了一个"Truncate"操作（Conway符号
t）（此球形映射为足球）。
我们应用了"Dual"运算符（Conway符号
d）。
我们再次应用了"Truncate"操作。此时配方为
tdtI（从右边阅读！）。你已经可以看到这个过程了。
重复步骤3和4，直到满意为止。
dtdtdtdtI 的网格示例。
这很容易实现。我建议使用数据结构，使得遍历相邻的顶点、边等变得容易，例如使用有向边或半边数据结构来处理您的网格。您只需要为您要查找的形状实现截取和对偶操作即可。- hkrish
5
这个方法是否允许我任意绘制球体的一个子部分？ - Aaron Franke
你可以生成整个物体，然后删除不需要的网格部分。甚至可以在其中一个双重操作之后尝试删除球体的部分——此时整个网格将变成三角形，然后进一步细化其余部分。 - hkrish
这并不理想。目标是获取球体上的六边形位置列表，获取顶点并绘制它们。我必须从小处开始，因为我考虑将它们用作行星，这需要许多递归级别，并且您只能看到其中的一部分。我无法承担计算“dtdtdtdtdtdtdtdtdtdtdtdtdtdtdtdtI”的成本。 - Aaron Franke
这真的很棒。你有没有想过如何在二维中索引三角形？经纬度可能不是最好的方法，因为单个补丁是“均匀分布”的。所以也许有一个“更好”的方法。 - Flinsch
1我想我找到了一些东西：“快速球形自组织映射-使用索引的测地数据结构”。 - Flinsch
25
首先，对问题中的图像进行分析：由相邻五边形中心组成的球面三角形似乎是等边的。当五个等边三角形在一个角相遇并覆盖整个球体时，只有一个二十面体可以产生这种配置。因此，有12个五边形和20个六边形网格的三角剪切块被映射到球体上。
因此，这是在球体上构建这样的六边形网格的一种方法：
1. 创建六边形网格的三角形剪裁：固定的三角形（我选择了(-0.5,0),(0.5,0),(0,sqrt(3)/2)）与所需分辨率
2. 计算二十面体的顶点并定义其20个三角形面（见下面的代码）。二十面体的顶点定义了五边形的中心，二十面体的面定义了映射六边形网格的剪切块。（二十面体将球面表面细分为三角形的最好的正则划分，即划分为相等的等边三角形。其他这样的划分可以从四面体或八面体中导出；然后在三角形的角上会有三角形或正方形。此外，更少更大的三角形将使平面网格映射到曲面上的任何扭曲更加明显。因此，选择二十面体作为三角形剪切块的基础有助于最小化六边形的扭曲。）
3. 将六边形网格的三角形剪切映射到对应于二十面体面的球面三角形：基于重心坐标系的双重球面线性插值即可完成。下面是一个分辨率为
这里是生成二十面体角点（坐标）和三角形（点索引）的Python代码：
因此，这是在球体上构建这样的六边形网格的一种方法：
1. 创建六边形网格的三角形剪裁：固定的三角形（我选择了(-0.5,0),(0.5,0),(0,sqrt(3)/2)）与所需分辨率
n的六边形网格重叠，使三角形的角与六边形中心重合，见n = 0,1,2,20的示例：
2. 计算二十面体的顶点并定义其20个三角形面（见下面的代码）。二十面体的顶点定义了五边形的中心，二十面体的面定义了映射六边形网格的剪切块。（二十面体将球面表面细分为三角形的最好的正则划分，即划分为相等的等边三角形。其他这样的划分可以从四面体或八面体中导出；然后在三角形的角上会有三角形或正方形。此外，更少更大的三角形将使平面网格映射到曲面上的任何扭曲更加明显。因此，选择二十面体作为三角形剪切块的基础有助于最小化六边形的扭曲。）3. 将六边形网格的三角形剪切映射到对应于二十面体面的球面三角形：基于重心坐标系的双重球面线性插值即可完成。下面是一个分辨率为
n = 10的六边形网格的三角形剪切映射到一个球面三角形（由二十面体的一个面定义），以及将该网格映射到覆盖整个球体的所有这些球面三角形的插图（不同的映射使用不同的颜色）：这里是生成二十面体角点（坐标）和三角形（点索引）的Python代码：
from math import sin,cos,acos,sqrt,pi
s,c = 2/sqrt(5),1/sqrt(5)
topPoints = [(0,0,1)] + [(s*cos(i*2*pi/5.), s*sin(i*2*pi/5.), c) for i in range(5)]
bottomPoints = [(-x,y,-z) for (x,y,z) in topPoints]
icoPoints = topPoints + bottomPoints
icoTriangs = [(0,i+1,(i+1)%5+1) for i in range(5)] +\
[(6,i+7,(i+1)%5+7) for i in range(5)] +\
[(i+1,(i+1)%5+1,(7-i)%5+7) for i in range(5)] +\
[(i+1,(7-i)%5+7,(8-i)%5+7) for i in range(5)]
以下是将固定三角形（点）映射到球面三角形的Python代码，使用双倍球面线性插值：
# barycentric coords for triangle (-0.5,0),(0.5,0),(0,sqrt(3)/2)
def barycentricCoords(p):
x,y = p
# l3*sqrt(3)/2 = y
l3 = y*2./sqrt(3.)
# l1 + l2 + l3 = 1
# 0.5*(l2 - l1) = x
l2 = x + 0.5*(1 - l3)
l1 = 1 - l2 - l3
return l1,l2,l3
from math import atan2
def scalProd(p1,p2):
return sum([p1[i]*p2[i] for i in range(len(p1))])
# uniform interpolation of arc defined by p0, p1 (around origin)
# t=0 -> p0, t=1 -> p1
def slerp(p0,p1,t):
assert abs(scalProd(p0,p0) - scalProd(p1,p1)) < 1e-7
ang0Cos = scalProd(p0,p1)/scalProd(p0,p0)
ang0Sin = sqrt(1 - ang0Cos*ang0Cos)
ang0 = atan2(ang0Sin,ang0Cos)
l0 = sin((1-t)*ang0)
l1 = sin(t *ang0)
return tuple([(l0*p0[i] + l1*p1[i])/ang0Sin for i in range(len(p0))])
# map 2D point p to spherical triangle s1,s2,s3 (3D vectors of equal length)
def mapGridpoint2Sphere(p,s1,s2,s3):
l1,l2,l3 = barycentricCoords(p)
if abs(l3-1) < 1e-10: return s3
l2s = l2/(l1+l2)
p12 = slerp(s1,s2,l2s)
return slerp(p12,s3,l3)
- coproc
5
这个方法允许我任意绘制球体的子部分吗？ - Aaron Franke
@AaronFranke 确定：网格是由连接点的线构成的。可以根据需要过滤点和线。 - coproc
大家好，有没有人有完整的Python代码，这将非常棒！感谢您的帮助。 - Jean-Eric
如何将球形三角形中的点映射到原始三角形中的点？@coproc - user14789259
类似于 def mapSphere2Gridpoint(p,s1,s2,s3) 的内容 # 将球面三角形中的点映射到原始三角形中的点[-0.5, 0]，[0.5, 0]，[0，sqrt(3)/2)] - user14789259
7
[全面重新编辑 2017年10月18日]
几何图形的存储由您负责。您可以将其存储在某种网格中，也可以即时生成。我更喜欢将其存储在两个表格中。其中一个包含所有顶点（无重复项），另一个包含每个六边形使用的点的6个索引和一些额外信息（例如球面位置），以方便后续处理。
现在来看如何生成它：
创建六边形三角形
大小应为球体的半径。不包括角落的六边形，并且跳过三角形的最后一行（在径向和轴向上都是这样），因为这会导致在连接三角形段时重叠。
将60度的六边形三角形转换为72度的扇形
简单地转换为极坐标 (
radius,angle)，将三角形居中在0度周围。然后乘以cos(angle)/cos(30)的半径将其转换为扇形。然后将角度缩放比例调整为72/60。这将使我们的三角形可连接…复制并旋转三角形以填充五个五边形部分
只需旋转第一个三角形的点并存储为新的三角形即可。
计算
z基于此 半球体的六角形贴片，您可以将2D地图中的距离转换为弧长，以尽可能地减小失真。
然而当我尝试它（下面的示例）时，六边形有点失真，因此深度和缩放需要进行一些微调。或者稍后进行后处理。
将半球形复制以形成一个球体
只需复制点/六边形并否定
z轴（或旋转180度，如果要保留绕组顺序）即可。添加赤道和所有丢失的五边形和六边形
您应该使用相邻六边形的坐标，以便不会给网格增加更多的失真和重叠。这里是预览：
蓝色是起始三角形。深蓝色是其副本。红色是极点五边形。暗绿色是赤道，浅绿色是三角形之间的连接线。在黄色的是靠近深橙色五边形的失踪赤道六边形。
这里是一个简单的C++ OpenGL示例（来自于#4中的链接）：
//$$---- Form CPP ----
//---------------------------------------------------------------------------
#include <vcl.h>
#include <math.h>
#pragma hdrstop
#include "win_main.h"
#include "gl/OpenGL3D_double.cpp"
#include "PolyLine.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TMain *Main;
OpenGLscreen scr;
bool _redraw=true;
double animx= 0.0,danimx=0.0;
double animy= 0.0,danimy=0.0;
//---------------------------------------------------------------------------
PointTab pnt; // (x,y,z)
struct _hexagon
{
int ix[6]; // index of 6 points, last point duplicate for pentagon
int a,b; // spherical coordinate
DWORD col; // color
// inline
_hexagon() {}
_hexagon(_hexagon& a) { *this=a; }
~_hexagon() {}
_hexagon* operator = (const _hexagon *a) { *this=*a; return this; }
//_hexagon* operator = (const _hexagon &a) { ...copy... return this; }
};
List<_hexagon> hex;
//---------------------------------------------------------------------------
// https://dev59.com/K1YN5IYBdhLWcg3w27cv#46787885
//---------------------------------------------------------------------------
void hex_sphere(int N,double R)
{
const double c=cos(60.0*deg);
const double s=sin(60.0*deg);
const double sy= R/(N+N-2);
const double sz=sy/s;
const double sx=sz*c;
const double sz2=0.5*sz;
const int na=5*(N-2);
const int nb= N;
const int b0= N;
double *q,p[3],ang,len,l,l0,ll;
int i,j,n,a,b,ix;
_hexagon h,*ph;
hex.allocate(na*nb);
hex.num=0;
pnt.reset3D(N*N);
b=0; a=0; ix=0;
// generate triangle hex grid
h.col=0x00804000;
for (b=1;b<N-1;b++) // skip first line b=0
for (a=1;a<b;a++) // skip first and last line
{
p[0]=double(a )*(sx+sz);
p[1]=double(b-(a>>1))*(sy*2.0);
p[2]=0.0;
if (int(a&1)!=0) p[1]-=sy;
ix=pnt.add(p[0]+sz2+sx,p[1] ,p[2]); h.ix[0]=ix; // 2 1
ix=pnt.add(p[0]+sz2 ,p[1]+sy,p[2]); h.ix[1]=ix; // 3 0
ix=pnt.add(p[0]-sz2 ,p[1]+sy,p[2]); h.ix[2]=ix; // 4 5
ix=pnt.add(p[0]-sz2-sx,p[1] ,p[2]); h.ix[3]=ix;
ix=pnt.add(p[0]-sz2 ,p[1]-sy,p[2]); h.ix[4]=ix;
ix=pnt.add(p[0]+sz2 ,p[1]-sy,p[2]); h.ix[5]=ix;
h.a=a;
h.b=N-1-b;
hex.add(h);
} n=hex.num; // remember number of hexs for the first triangle
// distort points to match area
for (ix=0;ix<pnt.nn;ix+=3)
{
// point pointer
q=pnt.pnt.dat+ix;
// convert to polar coordinates
ang=atan2(q[1],q[0]);
len=vector_len(q);
// match area of pentagon (72deg) triangle as we got hexagon (60deg) triangle
ang-=60.0*deg; // rotate so center of generated triangle is angle 0deg
while (ang>+60.0*deg) ang-=pi2;
while (ang<-60.0*deg) ang+=pi2;
len*=cos(ang)/cos(30.0*deg); // scale radius so triangle converts to pie
ang*=72.0/60.0; // scale up angle so rotated triangles merge
// convert back to cartesian
q[0]=len*cos(ang);
q[1]=len*sin(ang);
}
// copy and rotate the triangle to cover pentagon
h.col=0x00404000;
for (ang=72.0*deg,a=1;a<5;a++,ang+=72.0*deg)
for (ph=hex.dat,i=0;i<n;i++,ph++)
{
for (j=0;j<6;j++)
{
vector_copy(p,pnt.pnt.dat+ph->ix[j]);
rotate2d(-ang,p[0],p[1]);
h.ix[j]=pnt.add(p[0],p[1],p[2]);
}
h.a=ph->a+(a*(N-2));
h.b=ph->b;
hex.add(h);
}
// compute z
for (q=pnt.pnt.dat,ix=0;ix<pnt.nn;ix+=pnt.dn,q+=pnt.dn)
{
q[2]=0.0;
ang=vector_len(q)*0.5*pi/R;
q[2]=R*cos(ang);
ll=fabs(R*sin(ang)/sqrt((q[0]*q[0])+(q[1]*q[1])));
q[0]*=ll;
q[1]*=ll;
}
// copy and mirror the other half-sphere
n=hex.num;
for (ph=hex.dat,i=0;i<n;i++,ph++)
{
for (j=0;j<6;j++)
{
vector_copy(p,pnt.pnt.dat+ph->ix[j]);
p[2]=-p[2];
h.ix[j]=pnt.add(p[0],p[1],p[2]);
}
h.a= ph->a;
h.b=-ph->b;
hex.add(h);
}
// create index search table
int i0,i1,j0,j1,a0,a1,ii[5];
int **ab=new int*[na];
for (a=0;a<na;a++)
{
ab[a]=new int[nb+nb+1];
for (b=-nb;b<=nb;b++) ab[a][b0+b]=-1;
}
n=hex.num;
for (ph=hex.dat,i=0;i<n;i++,ph++) ab[ph->a][b0+ph->b]=i;
// add join ring
h.col=0x00408000;
for (a=0;a<na;a++)
{
h.a=a;
h.b=0;
a0=a;
a1=a+1; if (a1>=na) a1-=na;
i0=ab[a0][b0+1];
i1=ab[a1][b0+1];
j0=ab[a0][b0-1];
j1=ab[a1][b0-1];
if ((i0>=0)&&(i1>=0))
if ((j0>=0)&&(j1>=0))
{
h.ix[0]=hex[i1].ix[1];
h.ix[1]=hex[i0].ix[0];
h.ix[2]=hex[i0].ix[1];
h.ix[3]=hex[j0].ix[1];
h.ix[4]=hex[j0].ix[0];
h.ix[5]=hex[j1].ix[1];
hex.add(h);
ab[h.a][b0+h.b]=hex.num-1;
}
}
// add 2x5 join lines
h.col=0x00008040;
for (a=0;a<na;a+=N-2)
for (b=1;b<N-3;b++)
{
// +b hemisphere
h.a= a;
h.b=+b;
a0=a-b; if (a0< 0) a0+=na; i0=ab[a0][b0+b+0];
a0--; if (a0< 0) a0+=na; i1=ab[a0][b0+b+1];
a1=a+1; if (a1>=na) a1-=na; j0=ab[a1][b0+b+0];
j1=ab[a1][b0+b+1];
if ((i0>=0)&&(i1>=0))
if ((j0>=0)&&(j1>=0))
{
h.ix[0]=hex[i0].ix[5];
h.ix[1]=hex[i0].ix[4];
h.ix[2]=hex[i1].ix[5];
h.ix[3]=hex[j1].ix[3];
h.ix[4]=hex[j0].ix[4];
h.ix[5]=hex[j0].ix[3];
hex.add(h);
}
// -b hemisphere
h.a= a;
h.b=-b;
a0=a-b; if (a0< 0) a0+=na; i0=ab[a0][b0-b+0];
a0--; if (a0< 0) a0+=na; i1=ab[a0][b0-b-1];
a1=a+1; if (a1>=na) a1-=na; j0=ab[a1][b0-b+0];
j1=ab[a1][b0-b-1];
if ((i0>=0)&&(i1>=0))
if ((j0>=0)&&(j1>=0))
{
h.ix[0]=hex[i0].ix[5];
h.ix[1]=hex[i0].ix[4];
h.ix[2]=hex[i1].ix[5];
h.ix[3]=hex[j1].ix[3];
h.ix[4]=hex[j0].ix[4];
h.ix[5]=hex[j0].ix[3];
hex.add(h);
}
}
// add pentagons at poles
_hexagon h0,h1;
h0.col=0x00000080;
h0.a=0; h0.b=N-1; h1=h0; h1.b=-h1.b;
p[2]=sqrt((R*R)-(sz*sz));
for (ang=0.0,a=0;a<5;a++,ang+=72.0*deg)
{
p[0]=2.0*sz*cos(ang);
p[1]=2.0*sz*sin(ang);
h0.ix[a]=pnt.add(p[0],p[1],+p[2]);
h1.ix[a]=pnt.add(p[0],p[1],-p[2]);
}
h0.ix[5]=h0.ix[4]; hex.add(h0);
h1.ix[5]=h1.ix[4]; hex.add(h1);
// add 5 missing hexagons at poles
h.col=0x00600060;
for (ph=&h0,b=N-3,h.b=N-2,i=0;i<2;i++,b=-b,ph=&h1,h.b=-h.b)
{
a = 1; if (a>=na) a-=na; ii[0]=ab[a][b0+b];
a+=N-2; if (a>=na) a-=na; ii[1]=ab[a][b0+b];
a+=N-2; if (a>=na) a-=na; ii[2]=ab[a][b0+b];
a+=N-2; if (a>=na) a-=na; ii[3]=ab[a][b0+b];
a+=N-2; if (a>=na) a-=na; ii[4]=ab[a][b0+b];
for (j=0;j<5;j++)
{
h.a=((4+j)%5)*(N-2)+1;
h.ix[0]=ph->ix[ (5-j)%5 ];
h.ix[1]=ph->ix[ (6-j)%5 ];
h.ix[2]=hex[ii[(j+4)%5]].ix[4];
h.ix[3]=hex[ii[(j+4)%5]].ix[5];
h.ix[4]=hex[ii[ j ]].ix[3];
h.ix[5]=hex[ii[ j ]].ix[4];
hex.add(h);
}
}
// add 2*5 pentagons and 2*5 missing hexagons at equator
h0.a=0; h0.b=N-1; h1=h0; h1.b=-h1.b;
for (ang=36.0*deg,a=0;a<na;a+=N-2,ang-=72.0*deg)
{
p[0]=R*cos(ang);
p[1]=R*sin(ang);
p[2]=sz;
i0=pnt.add(p[0],p[1],+p[2]);
i1=pnt.add(p[0],p[1],-p[2]);
a0=a-1;if (a0< 0) a0+=na;
a1=a+1;if (a1>=na) a1-=na;
ii[0]=ab[a0][b0-1]; ii[2]=ab[a1][b0-1];
ii[1]=ab[a0][b0+1]; ii[3]=ab[a1][b0+1];
// hexagons
h.col=0x00008080;
h.a=a; h.b=0;
h.ix[0]=hex[ii[0]].ix[0];
h.ix[1]=hex[ii[0]].ix[1];
h.ix[2]=hex[ii[1]].ix[1];
h.ix[3]=hex[ii[1]].ix[0];
h.ix[4]=i0;
h.ix[5]=i1;
hex.add(h);
h.a=a; h.b=0;
h.ix[0]=hex[ii[2]].ix[2];
h.ix[1]=hex[ii[2]].ix[1];
h.ix[2]=hex[ii[3]].ix[1];
h.ix[3]=hex[ii[3]].ix[2];
h.ix[4]=i0;
h.ix[5]=i1;
hex.add(h);
// pentagons
h.col=0x000040A0;
h.a=a; h.b=0;
h.ix[0]=hex[ii[0]].ix[0];
h.ix[1]=hex[ii[0]].ix[5];
h.ix[2]=hex[ii[2]].ix[3];
h.ix[3]=hex[ii[2]].ix[2];
h.ix[4]=i1;
h.ix[5]=i1;
hex.add(h);
h.a=a; h.b=0;
h.ix[0]=hex[ii[1]].ix[0];
h.ix[1]=hex[ii[1]].ix[5];
h.ix[2]=hex[ii[3]].ix[3];
h.ix[3]=hex[ii[3]].ix[2];
h.ix[4]=i0;
h.ix[5]=i0;
hex.add(h);
}
// release index search table
for (a=0;a<na;a++) delete[] ab[a];
delete[] ab;
}
//---------------------------------------------------------------------------
void hex_draw(GLuint style) // draw hex
{
int i,j;
_hexagon *h;
for (h=hex.dat,i=0;i<hex.num;i++,h++)
{
if (style==GL_POLYGON) glColor4ubv((BYTE*)&h->col);
glBegin(style);
for (j=0;j<6;j++) glVertex3dv(pnt.pnt.dat+h->ix[j]);
glEnd();
}
if (0)
if (style==GL_POLYGON)
{
scr.text_init_pixel(0.1,-0.2);
glColor3f(1.0,1.0,1.0);
for (h=hex.dat,i=0;i<hex.num;i++,h++)
if (abs(h->b)<2)
{
double p[3];
vector_ld(p,0.0,0.0,0.0);
for (j=0;j<6;j++)
vector_add(p,p,pnt.pnt.dat+h->ix[j]);
vector_mul(p,p,1.0/6.0);
scr.text(p[0],p[1],p[2],AnsiString().sprintf("%i,%i",h->a,h->b));
}
scr.text_exit_pixel();
}
}
//---------------------------------------------------------------------------
void TMain::draw()
{
scr.cls();
int x,y;
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.0,0.0,-5.0);
glRotated(animx,1.0,0.0,0.0);
glRotated(animy,0.0,1.0,0.0);
hex_draw(GL_POLYGON);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.0,0.0,-5.0+0.01);
glRotated(animx,1.0,0.0,0.0);
glRotated(animy,0.0,1.0,0.0);
glColor3f(1.0,1.0,1.0);
glLineWidth(2);
hex_draw(GL_LINE_LOOP);
glCirclexy(0.0,0.0,0.0,1.5);
glLineWidth(1);
scr.exe();
scr.rfs();
}
//---------------------------------------------------------------------------
__fastcall TMain::TMain(TComponent* Owner) : TForm(Owner)
{
scr.init(this);
hex_sphere(10,1.5);
_redraw=true;
}
//---------------------------------------------------------------------------
void __fastcall TMain::FormDestroy(TObject *Sender)
{
scr.exit();
}
//---------------------------------------------------------------------------
void __fastcall TMain::FormPaint(TObject *Sender)
{
_redraw=true;
}
//---------------------------------------------------------------------------
void __fastcall TMain::FormResize(TObject *Sender)
{
scr.resize();
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(60,float(scr.xs)/float(scr.ys),0.1,100.0);
_redraw=true;
}
//-----------------------------------------------------------------------
void __fastcall TMain::Timer1Timer(TObject *Sender)
{
animx+=danimx; if (animx>=360.0) animx-=360.0; _redraw=true;
animy+=danimy; if (animy>=360.0) animy-=360.0; _redraw=true;
if (_redraw) { draw(); _redraw=false; }
}
//---------------------------------------------------------------------------
void __fastcall TMain::FormKeyDown(TObject *Sender, WORD &Key, TShiftState Shift)
{
Caption=Key;
if (Key==40){ animx+=2.0; _redraw=true; }
if (Key==38){ animx-=2.0; _redraw=true; }
if (Key==39){ animy+=2.0; _redraw=true; }
if (Key==37){ animy-=2.0; _redraw=true; }
}
//---------------------------------------------------------------------------
我知道这个索引有点混乱，而且由于我懒得制作统一的索引方式，螺旋规则也不能保证。注意每个六边形的a索引不是线性的，如果你想用它们来映射到2D地图上，您需要使用atan2在其中心点位置的x，y上重新计算它。
预览如下：
仍然存在一些扭曲。它们的原因是我们使用5个三角形在赤道连接（所以连接是保证的）。这意味着周长是5*R而不是6.28*R。然而，这可以通过场模拟进一步改进。只需取所有点并添加基于它们之间距离的拉力和约束在球面表面上。运行模拟，当振荡降至阈值以下时，您就得到了您的球格网...
另一个选择是找到一些方程来重新映射网格点（类似于我为三角形到扇区转换所做的方式），这将产生更好的结果。
- Spektre
16
1@meowgoesthedog 我正在调整它...并且已经获得了更好的结果（使用10个方向度量而不是5个），但是六边形会有一些畸变...这可以通过场模拟后期处理。 - Spektre
1@meowgoesthedog，我已经添加了新的预览图，但是它仍然不如我想要的那样好。由于五边形的周长(
5*R)与六边形的周长(6R)相比距离6.28*R更远，因此扭曲程度很高... - Spektre1@meowgoesthedog 我之前也尝试过这个，可以看看这个例子 如何将圆柱体变成没有极点的球体。这个例子并不是以二十面体为起始形状，而是为了更兼容六边形输出而进行了扭曲。这种方法的问题在于你必须使用正确的起始形状和递归次数才能与六边形网格兼容。即使三角形完美，决定拓扑结构也非常困难。而且二十面体虽然导致了几乎完美的三角形，但也带来了很多其他问题。 - Spektre
1@AaronFranke，虽然模拟结果看起来好了一些，但还不够。不过我有一个更简单的想法，可以直接处理曲率，而不需要复制和旋转等操作...只使用球面坐标系。需要先编写代码来验证我的想法是否正确... - Spektre
2用五个三角形修补半个球会使它们不等边。从OP的图像中可以猜测这些三角形是等边的。近距离摄像机的视角可能会让人误以为一个五边形周围的五个三角形覆盖了半个球，但实际上有20个三角形 - 对应于二十面体的20个面。请参见我回答中的20个三角形补丁的图像。 - coproc
显示剩余11条评论
网页内容由stack overflow 提供, 点击上面的可以查看英文原文，
原文链接
原文链接