logo标签列表

在R中计算一个圆的半径的倒数的逆。

pythonrgeometrycurve
3
我正在尝试复制一项研究中使用的函数，但实际上没有数学背景来充分了解应该如何完成。该度量取自舌轮廓的三个点，并使用这三个点计算通过它们的圆的半径。我在这里找到了一个使用Python实现此功能的工具。我已经尝试修改代码，以便使用我的数据在R中运行。（发布在底部）
问题是，根据我正在阅读的研究，然后需要计算圆周的凹度并找到通过三个点的圆的半径的倒数。我正在搜索和搜索，但老实说这对我来说毫无意义。我唯一发现的是，我似乎需要计算舌面曲线的一阶和二阶导数。我真的希望有人能够帮助探索如何在R中执行此操作。坦率地说，我对理解这里的数学并不是特别感兴趣，只是想知道如何实际实现它。
编辑：我认为下面是我需要复制的公式。正如MBo指出的那样，情况并非如此。

Here is the formula I need to replicate

如果有帮助的话，我会重复另一项研究中使用非常相似方法的内容。

“任何三个点（A、B、C）都可以被看作位于圆周上。圆将有一个半径，其倒数代表通过这三个点的圆的曲率。”这组三个点“产生了一个曲率数字，它是通过它们的圆的半径的倒数。沿直线排列的三个点的曲率为零，因为它们的凹度为零，这成为曲率方程的分子”。这就是我需要做的事情，但不知道从哪里开始在R中操作。

下面的代码是我正在尝试在R中复制以获得三个点的半径的Python代码。在那之后，我不知道该怎么做。

def define_circle(p1, p2, p3):
    """
    Returns the center and radius of the circle passing the given 3 points.
    In case the 3 points form a line, returns (None, infinity).
    """
    temp = p2[0] * p2[0] + p2[1] * p2[1]
    bc = (p1[0] * p1[0] + p1[1] * p1[1] - temp) / 2
    cd = (temp - p3[0] * p3[0] - p3[1] * p3[1]) / 2
    det = (p1[0] - p2[0]) * (p2[1] - p3[1]) - (p2[0] - p3[0]) * (p1[1] - p2[1])

    if abs(det) < 1.0e-6:
        return (None, np.inf)

    # Center of circle
    cx = (bc*(p2[1] - p3[1]) - cd*(p1[1] - p2[1])) / det
    cy = ((p1[0] - p2[0]) * cd - (p2[0] - p3[0]) * bc) / det

    radius = np.sqrt((cx - p1[0])**2 + (cy - p1[1])**2)
    return ((cx, cy), radius)

这是我的R尝试。 我还没有编写函数，但我会查看曲线上的三个点A、B和C。该函数将提取每个点的x和y值（称为x_value_a、y_value_a等）。完成此操作后，我将运行以下代码。在此之后，我完全被难住了。

temp = x_value_b ^ 2 + y_value_b ^ 2

bc = (x_value_a ^ 2 + y_value_a ^ 2 - temp) / 2

cd = (temp - x_value_c ^ 2 - y_value_c ^ 2) / 2

det = (x_value_a - x_value_b) * (y_value_b - y_value_c) - (x_value_b - x_value_c) * (y_value_a - y_value_b)

cx = (bc * (y_value_b - y_value_c) - cd * (y_value_a - y_value_b)) / det 

cy = ((x_value_a - x_value_b) * cd - (x_value_b - x_value_c) * bc) / det

radius = sqrt((cx - x_value_a)^2 + (cy - y_value_a)^2)

非常感谢您的帮助。对于我的数学无知，我感到抱歉。

1
C（解析曲线的曲率）的公式与您的问题无关。 - MBo
1
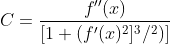
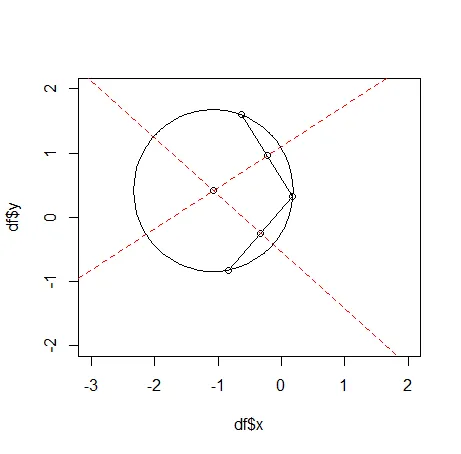
我的第一反应是，通过“inverse”，他们的意思是“倒数”-所以你只需要1 / radius。这将与直线的凹度为0相吻合，因为半径是无限的。 - Hobo
1
顺便提一下，你的 R 代码中好像缺少 - temp 来计算 bc。 - Hobo
@MBo，感谢您指出这一点。曲率测量在我阅读的一篇论文中似乎很重要。我想使用的测量基于那个测量，所以我认为在这里计算是必要的。很高兴我错了，不必继续追求那个方向了。谢谢！ - BubbleMaus
1
@Hobo，感谢您的两条评论。我已经更新了代码以包含缺失的值（很好的发现！）。我希望您对1/半径的看法是正确的。 - BubbleMaus
4个回答
3
如果你只需要将Python脚本翻译成R，那就非常简单（我不是很理解为什么你在添加的R代码中要把它分开）。
define_circle = function(p1, p2, p3) {

  # Returns the center and radius of the circle passing the given 3 points.
  # In case the 3 points form a line, returns warning.
  
  temp = p2[1] * p2[1] + p2[2] * p2[2]
  bc = (p1[1] * p1[1] + p1[2] * p1[2] - temp) / 2
  cd = (temp - p3[1] * p3[1] - p3[2] * p3[2]) / 2
  det = (p1[1] - p2[1]) * (p2[2] - p3[2]) - (p2[1] - p3[1]) * (p1[2] - p2[2])
  
  if (abs(det) < 1.0e-6) {
    
    return(c("Three points form a line"))
    
  } else {
    
    # Center of circle
    cx = (bc*(p2[2] - p3[2]) - cd*(p1[2] - p2[2])) / det
    cy = ((p1[1] - p2[1]) * cd - (p2[1] - p3[1]) * bc) / det
    
    radius = sqrt((cx - p1[1])**2 + (cy - p1[2])**2)
    
    return(list("center" = c(cx, cy), "radius" = radius))
    
  }

}

请注意，p1-3表示一个包含x和y坐标的向量。我必须相信原始的Python代码，但使用desmos.com进行快速检查似乎表明它有效：
> define_circle(c(0,1), c(2,2), c(0.5,5))
$center
[1] 0.25 3.00

$radius
[1] 2.015564

示例圆形图

只需保持函数不变，您就可以计算任何要素集的半径倒数。我同意半径倒数简单地意味着 1/半径。

感谢您的回复，Bert。您将代码翻译成与原始代码匹配的形式是有道理的。我只是手动分离了所有的x和y值，所以它看起来很丑，可能需要更多的解释。我也没有使用if和else，但我应该包括它们，以防万一，所以我一定会借鉴您的代码。不幸的是，主要问题不是将Python代码翻译成R代码，所以我不能将其选为答案，但我非常感谢您的回复。 - BubbleMaus
2
这是一种几何方法。假设我有一个数据框中的三个随机点：
set.seed(1)

df <- setNames(as.data.frame(matrix(rnorm(6), nrow = 3)), c("x", "y"))
df
#>            x          y
#> 1 -0.6264538  1.5952808
#> 2  0.1836433  0.3295078
#> 3 -0.8356286 -0.8204684

plot(df$x, df$y, xlim = c(-3, 2), ylim = c(-2, 2))

enter image description here

现在，我可以在这些点之间画线，并算出中点的算术平均值：
lines(df$x, df$y)

mid_df <- data.frame(x = diff(df$x)/2 + df$x[-3],
                     y = diff(df$y)/2 + df$y[-3],
                     slope = -diff(df$x)/diff(df$y))
mid_df$intercept <- mid_df$y - mid_df$slope * mid_df$x

points(mid_df$x, mid_df$y)

enter image description here

如果我通过中点画出垂直于这些线的线条，那么得到的点应该与我的三个起始点等距离。
abline(a = mid_df$intercept[1], b = mid_df$slope[1], col = "red", lty = 2)
abline(a = mid_df$intercept[2], b = mid_df$slope[2], col = "red", lty = 2)

center_x <- (mid_df$intercept[2] - mid_df$intercept[1]) /
            (mid_df$slope[1] - mid_df$slope[2])

center_y <- mid_df$slope[1] * center_x + mid_df$intercept[1]

points(center_x, center_y)

enter image description here

确实如此：
distances <- sqrt((center_x - df$x)^2 + (center_y - df$y)^2)

distances
#> [1] 1.136489 1.136489 1.136489

因此，圆的半径由distances [1]给出，其中心位于center_x，center_y。你最终得到的曲率由1 / distances [1]给出。
为了证明这一点，让我们画出描述的圆：
xvals <- seq(center_x - distances[1], center_x + distances[1], length.out = 100)
yvals <- center_y + sqrt(distances[1]^2 - (xvals - center_x)^2)
yvals <- c(yvals, center_y - sqrt(distances[1]^2 - (xvals - center_x)^2))
xvals <- c(xvals, rev(xvals))
lines(xvals, yvals)

enter image description here

非常感谢您提供如此详尽的回复。以这种方式呈现真是太美妙了。 - BubbleMaus
可爱的解释 - Hobo
1
我最喜欢的分辨率是：

  • subtract the coordinates of one point from the two others;

  • now your circle is through the origin and has the simplified equation

    2 Xc X + 2 Yc Y = X² + Y²

  • you have a standard and easy system of two equations in two unknowns.

    X1 Xc + Y1 Yc = (X1² + Y1²) / 2 = Z1
X2 Xc + Y2 Yc = (X2² + Y2²) / 2 = Z2

  • when you have computed Xc and Yc, the radius is √Xc²+Yc².

0

使用复数：

我们通过变换 Z = (2Z - Z1 - Z2) / (Z2 - Z1) 将点 Z1、Z2 映射到 -1 和 1。现在圆的中心在虚轴上，设为 iH。我们表达出圆心与 1 和第三个点 (2 Z3 - Z0 - Z1) / (Z1 - Z0) = X + iY 等距。

H² + 1 = X² + (Y - H)²

或者

H = (X² + Y² - 1) / 2Y

并且

R = √H²+1.
网页内容由stack overflow 提供, 点击上面的
可以查看英文原文，
原文链接