将双曲线转换为贝塞尔曲线以绘制轨道路径图。

Question

我正在使用HTML canvas编写一个2D模拟器和游戏，涉及到轨道力学。程序的一个功能是在某一点获取卫星的位置和速度向量，并返回绕一个行星的2D轨道的半长轴、离心率、近地点幅角等信息。当离心率小于1时，我可以很容易地使用ctx.ellipse()将轨道绘制成椭圆形。然而，在离心率大于1时，正确的轨道形状是双曲线。目前，如果离心率大于1，我的程序就什么都不画，但我希望它能够绘制正确的双曲线轨道。由于没有内置的“双曲线”函数，我需要将我的轨道转换为贝塞尔曲线。我有点茫然不知如何做。输入应该是一个焦点的位置、半长轴、离心率和近地点幅角（基本上是轨道的旋转程度），并且应该返回正确的控制点以绘制双曲线估计曲线。它不必完全完美，只要足够接近即可。我该如何解决这个问题？

- Adam Kaufman

---

在椭圆或双曲线上取样几个点，并创建Catmull-Rom样条。每个Catmull-Rom样条段都是一个三次贝塞尔曲线。 - fang

展示你的代码，也许我们可以帮助你修复它。 - Mark Schultheiss

Answer 1

在锥面曲线方面，双曲线是Canvas无法本地呈现的一类曲线，因此您只能通过近似所需的曲线来实现。这里有一些选择：

1. 通过在距离上采样双曲线上的一个或两个点和极值附近的大量点来扁平化您的曲线，以便您可以绘制一个简单的多边形，看起来像曲线。

2. 使用单个“最佳逼近”二次或三次曲线对双曲线进行建模。

3. 如@fang所述：在几个点处对曲线进行采样，并将Catmull-Rom样条转换为Bezier形式。

4. 结合方法1和2。使用单个Bezier曲线来近似实际看起来弯曲的双曲线部分，并使用直线来表示不弯曲的部分。

5. 结合方法1和3，使用Catmull-Rom样条表示弯曲的部分，使用直线表示直的部分。

1：曲线扁平化

曲线扁平化基本上是微不足道的。旋转您的曲线直到它与轴对齐，然后使用标准双曲线函数计算给定x的y，其中a是极值之间距离的一半，b是半短轴。

x²/a² - y²/b² = 1
x²/a² = 1 + y²/b² 
x²/a² - 1 = y²/b² 
b²(x²/a² - 1) = y²
b²(x²/a² - 1) = y²
± sqrt(b²(x²/a² - 1)) = y

插入您的数值，迭代 x 来获取一系列 (x,y) 坐标（记得在极值附近生成更多坐标），然后将其转换为第一个坐标的 moveTo()，再跟随所需的 lineTo() 调用。只要点密度足够高以适应您呈现的比例，这就应该看起来不错。

function flattenHyperbola(a, b, inf=1000) {
  const points = [],
        a2 = a**2,
        b2 = b**2;

  let x, y, x2;

  for (x=inf; x>0.1; x/=2) {
    x2 = (a+x)**2;
    y = -Math.sqrt(b2*x2/a2 - b2);
    points.push({x: a+x, y});
  }

  points.push({x:a, y:0});

  for (x=0.1; x<inf; x*=2) {
    x2 = (a+x)*(a+x);
    y = Math.sqrt(b2*x2/a2 - b2);
    points.push({x:  a+x, y});
  }

  return points;
}

让我们将双曲线用红色绘制，近似曲线用蓝色绘制：

当然，这种方法的缺点是您需要为用户可能查看您的图形的每个比例创建一个单独的平滑曲线。或者，您需要生成一个有很多点的平滑曲线，然后根据放大/缩小程度跳过坐标来绘制它。

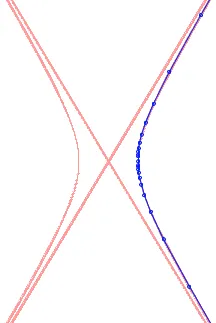
贝塞尔逼近

双曲线的参数表示为f(t)=(a*sec(t), b*tan(t))（或者更确切地说，这是y轴对齐的双曲线的表示法 - 我们可以通过应用标准旋转变换得到任何其他变体）。我们可以快速查看这些函数的泰勒级数，以确定我们可以使用哪个阶段的贝塞尔曲线：

sec(t) = 1 + t²/2 + 5t⁴/15 + ...
tan(t) = x + t³/3 + 2t⁵/15 + ...

因此，在每个维度上，我们可能只需要前两个项，这种情况下我们可以使用立方Bezier曲线（因为最高阶是t³）：

事实证明，这并不可行：它太不准确了，所以我们需要更好的近似方法：我们创建一个贝塞尔曲线，起点和终点“远离距离”，控制点设置使贝塞尔中点与双曲线的极值重合。如果我们尝试这样做，可能会被误导以为这样就可以解决问题：

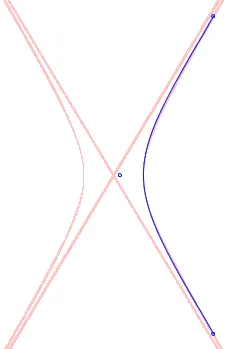
但是如果我们选择足够远的x，我们会发现这个近似值很快就不再起作用：

function touchingParabolicHyperbola(a, b, inf=1000) {
  const beziers = [],
        a2 = a**2,
        b2 = b**2;

  let x, x2, y, A, CA;

  for(x=50; x<inf; x+=50) {
    x2 = x**2;
    y = sqrt(b2*x2/a2 - b2);

    // Hit up https://pomax.github.io/bezierinfo/#abc
    // and model the hyperbola in the cubic graphic to
    // understand why the next, very simple-looking,
    // line actually works:
    A = a - (x-a)/3;

    // We want the control points for this A to lie on
    // the asymptote, but for small x we want it to be 0,
    // otherwise the curve won't run parallel to the
    // hyperbola at the start and end points.
    CA = lerp(0, A*b/a, x/inf);

    beziers.push([
      {x,    y: -y}, 
      {x: A, y:-CA}, 
      {x: A, y: CA}, 
      {x,    y}, 
    ]);
  }

  return beziers;
}

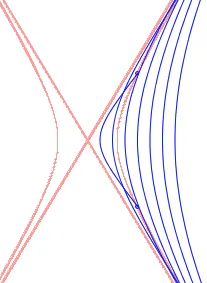
这向我们展示了一系列曲线，开始看起来还不错，但很快就变得完全无用了：

一个明显的问题是曲线最终会超过渐近线。我们可以通过强制控制点为(0,0)，使得Bezier外壳成为三角形，从而保证曲线始终在其中。

function tangentialParabolicHyperbola(a, b, inf=1000) {
  const beziers = [],
        a2 = a**2,
        b2 = b**2;

  let x, x2, y;

  for(x=50; x<inf; x+=50) {
    x2 = x**2;
    y = sqrt(b2*x2/a2 - b2);  
    beziers.push([
      {x, y:-y}, 
      {x: 0, y:0}, 
      {x: 0, y:0}, 
      {x, y}, 
    ]);
  }

  return beziers;
}

这导致一系列曲线从一个方面无用到另一个方面无用：

所以，单曲线逼近并不十分理想。如果我们使用更多的曲线呢？

3：使用Catmull-Rom样条的Poly-Bezier 我们可以通过在双曲线上使用多个Bezier曲线来克服上述问题，我们可以（几乎是微不足道的）通过选择双曲线上的一些坐标，然后构建通过这些点的Catmull-Rom样条来计算它们。由于通过N个点的Catmull-Rom样条等价于由N-3个线段组成的Poly-Bezier，因此这可能是获胜策略。

function hyperbolaToPolyBezier(a, b, inf=1000) {
  const points = [],
        a2 = a**2,
        b2 = b**2,
        step = inf/10;

  let x, y, x2,
   
  for (x=a+inf; x>a; x-=step) {
    x2 = x**2;
    y = -Math.sqrt(b2*x2/a2 - b2);
    points.push({x, y});
  }

  for (x=a; x<a+inf; x+=step) {
    x2 = x**2;
    y = Math.sqrt(b2*x2/a2 - b2);
    points.push({x, y});
  }

  return crToBezier(points);
}

使用转换函数，其定义如下：

function crToBezier(points) {
  const beziers = [];

  for(let i=0; i<points.length-3; i++) {
    //  NOTE THE i++ HERE! We're performing a sliding window conversion.
    let [p1, p2, p3, p4] = points.slice(i);
    beziers.push({
      start: p2,
      end: p3,
      c1: { x: p2.x + (p3.x-p1.x)/6, y: p2.y + (p3.y-p1.y)/6 },
      c2: { x: p3.x - (p4.x-p2.x)/6, y: p3.y - (p4.y-p2.y)/6 }
    })
  }

  return beziers;
}

让我们绘制出来：

我们需要比展平更多的工作，但好处是我们现在有了一条曲线，在任何比例下都“看起来像一条曲线”。

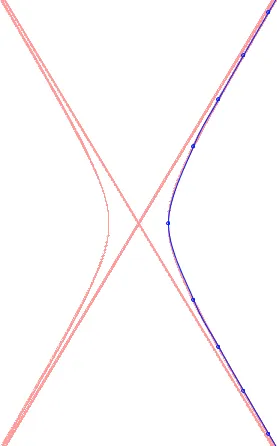
4：结合（1）和（2）

现在，大多数双曲线实际上“看起来很直”，因此对于那些部分使用大量的贝塞尔曲线感觉有点愚蠢：为什么不仅使用曲线来建模弯曲的部分，而使用直线来建模直的部分？

我们已经看到，如果将控制点固定为（0,0），可能会有一个相当不错的曲线，因此让我们结合方法1和2，创建一个单独的贝塞尔曲线，其起始点和结束点“足够接近”曲线，并将两条线段附加到曲线的末端，以连接渐近线上的两个远点（它们位于y=±b/a * x，因此x的任何大值都将产生可用的y）。

当然，诀窍是“找到”单曲线仍然捕捉到曲率，同时使我们的无限线看起来像顺畅地连接到我们的单曲线。再次使用贝塞尔projection identity很方便：我们希望A在（0,0）处，我们希望贝塞尔中点在（a,0）处，这意味着我们的起始和结束点应该具有x坐标为4a：

function hyperbolicallyFitParabolica(a, b, inf=1000) {
  const a2 = a**2,
        b2 = b**2,
        x = 4*a,
        x2 = x**2,
        y = sqrt(b2*x2/a2 - b2)
        bezier = [
          {x: x, y:-y}, 
          {x: 0, y: 0}, 
          {x: 0, y: 0}, 
          {x: x, y: y}, 
        ],
        start = { x1:x, y1:-y, x2:inf, y2: -inf * b/a},
        end   = { x1:x, y1: y, x2:inf, y2:  inf * b/a};

  return [start, bezier, end];
}

这给我们带来了以下结果（蓝色为Bezier曲线，黑色为线段）：

所以这并不是很好，但也不是太糟糕。如果观众不仔细检查渲染，那么肯定足够好，而且肯定很便宜，但我们只需再多做一点工作就可以做得更好。因此，让我们也看一下在这里可能能够想出的最佳近似：

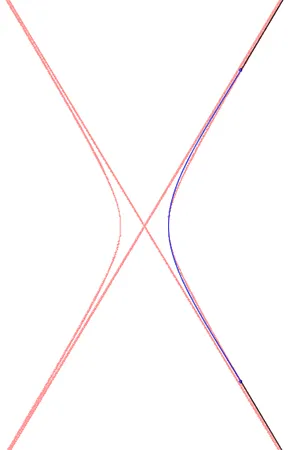
5：组合（1）和（3）

如果单个贝塞尔曲线无法使用，并且我们已经看到使用 Catmull-Rom 样条而不是单个曲线要好得多，那么当然我们也可以将方法 1 和 3 相结合。我们可以通过构造两条贝塞尔曲线而不是一条来在极值周围形成更好的拟合，通过生成以极值为中心的五个点，并将结果 Catmull-Rom 样条转换为 Bezier 形式：

function probablyTheBestHyperbola(a, b, inf=1000) {
  let curve = [],
      a2 = a**2,
      b2 = b**2,
      x, y, x2,
      cover = 100;

  // generate two points approaching the midpoint
  for (x=a+cover; x>a; x-=cover/2) {
    x2 = x**2;
    y = -Math.sqrt(b2*x2/a2 - b2);
    curve.add(new Vec2(x, y));
  }

  // generate three points departing at the midpoint
  for (x=a; x<=a+cover; x+=cover/2) {
    x2 = x*x;
    y = sqrt(b2*x2/a2 - b2);
    curve.add(new Vec2(x, y));
  }

  const beziers = crToBezier(curve),
        start = {
          x1: points.get(1).x, y1: points.get(1).y,
          x2: inf, y2: -inf * b/a
        },
        end = {
          x1: points.get(3).x, y1: points.get(3).y,
          x2: inf, y2: inf * b/a
        };

  return { start, beziers, end };
}

这给我们带来了以下结果（蓝色为CR，黑色为线段）：

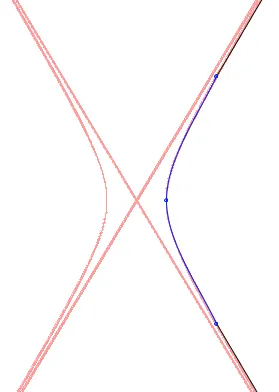
而这可能是在“计算便宜”、“易于扩展”和“外观正确性”之间取得平衡的最佳选择。

- Mike 'Pomax' Kamermans

Answer 2

我正在做几乎完全相同的事情，只是我使用SVG而不是画布。据我回忆，它们足够相似，以至于这是适用的。实际上，这涉及到贝塞尔曲线的一般性质，因此应用程序不应该有任何影响，除了注意a和y的符号（在图形应用程序与纯数学中倒置）。

请注意，这是以双曲线以原点为中心，而不是焦点。我建议以这种方式编码，然后根据需要使用变换进行定位和旋转。我在Desmos中进行了很多尝试，确切的图形在这里，但我不确定是否有效。

我用两种不同的方法做到了这一点。一种使用二次曲线，另一种使用三次曲线。两者都使用b，即sqrt(c^2-a^2)，而不是e，但很容易计算。

三次曲线

我将三次曲线设置为适合从2a到a的双曲线，这应该足以覆盖曲率明显的部分。由于顶点在中点，因此很容易设置控制点的x值。Y值有些棘手，但结果相当优雅。

三次曲线

控制点为

P1 = (2 * a, b * sqrt(3) )
P2 = (2/3 * a, b * (48-26 * sqrt(3) ) / 18
P3 = (2/3 * a, -b * (48-26 * sqrt(3) )/ 18
P4 = (2 *a, -b * sqrt(3) )

对我来说，这是更好的选择。如果你只需要一半的双曲线，比如从停车轨道到弹出轨道，那么你可以将其剪切。

二次曲线

二次曲线图片

要使用二次曲线进行弹出轨道，注意到离开时的切线是垂直的，在真近点角为90度时，y值是参数和飞行路径角，即切线，减小到tan(phi) = e。控制点是切线的交点，因此：

P1 = (a, 0)
P2 = (a,-e(a + c) + p
P3 = (c, p)

对我来说，这条曲线有点太短了。我试图添加额外的点来延长它，但是很难弄对。

其他选项

另一个选择是创建一条曲线并使用变换来改变大小和形状。显然，通过仿射变换可以从任何一条曲线创建任何其他曲线。还可以将曲线分成两条曲线并更改曲线的顺序。

- nomad

---

“显然，通过仿射变换可以从任何一条曲线创建另一条曲线”是错误的。贝塞尔曲线和圆弧都是曲线，无论进行多少次仿射变换都不能将一个曲线转化为另一个曲线。即使只考虑贝塞尔曲线，也是错误的，因为仿射变换不能将两个不同的坐标转换为相同的值，所以我们不能在两条曲线{p1，p2，p3，p4}之间进行转换，其中曲线一具有四个不同的值，而曲线二具有p2 = p3（这是一个非常常见的退化情况）。 - Mike 'Pomax' Kamermans

@Mike'Pomax'Kamermans 感谢您的澄清。我之前用“显然”作为开头是因为在研究这个问题时我并没有完全理解它。此外，在重新阅读时，我使用了“曲线”这个术语不太明确。根据维基百科，任何双曲线都可以表示为单位双曲线的仿射变换，那么是否可以说任何表示单位双曲线的贝塞尔曲线都可以被转换为表示任何双曲线？ - nomad

贝塞尔曲线在仿射变换下是不变的（这意味着对坐标应用仿射变换并使用这些转换后的坐标绘制曲线等价于对所有在曲线上的点应用相同的仿射变换），因此，如果您有一个近似（一半）单位双曲线的贝塞尔曲线，则可以进行仿射变换 _考虑舍入误差_，因为对单位双曲线的任何逼近误差都将被缩放倍增。 - Mike 'Pomax' Kamermans