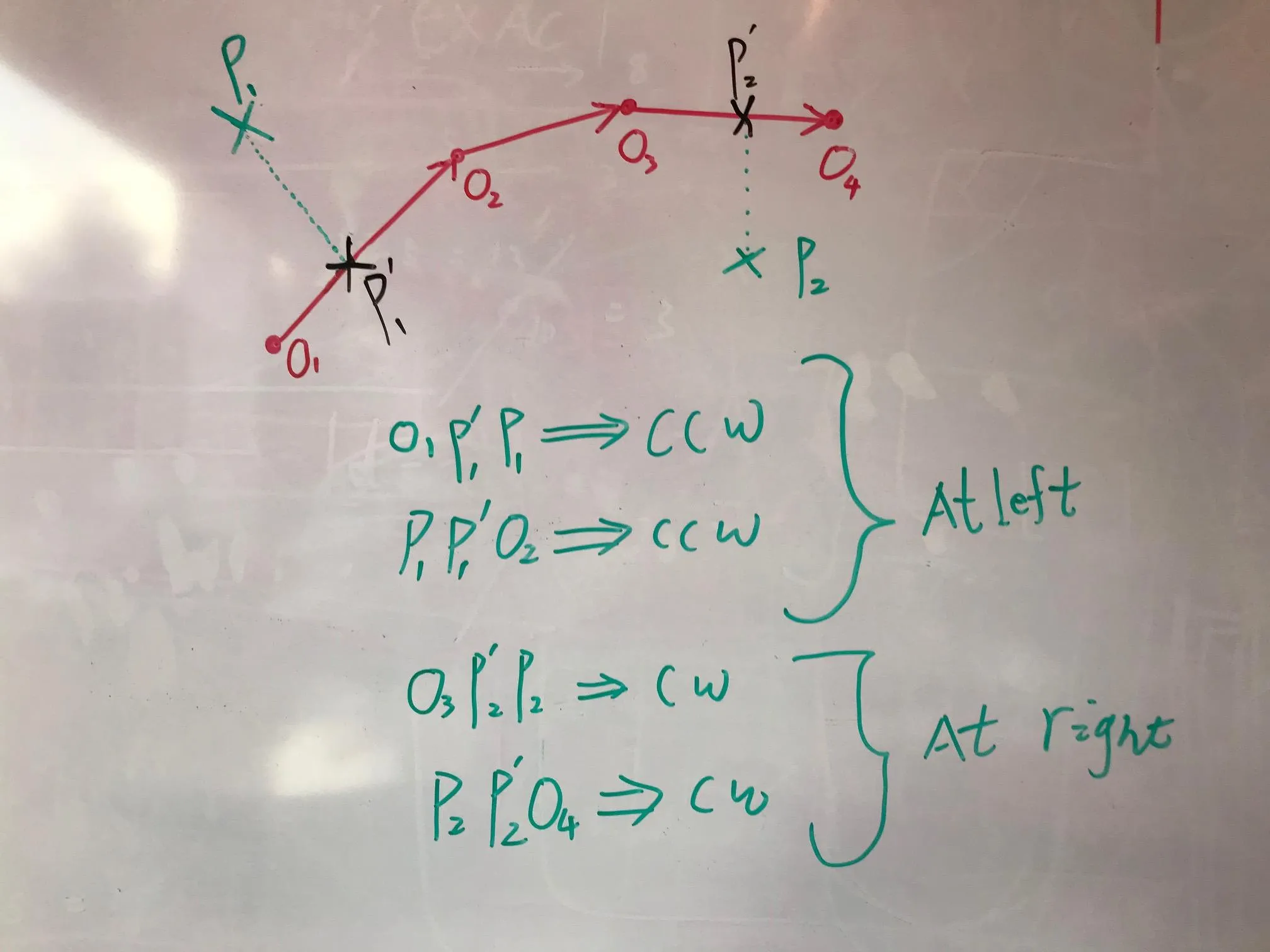我正在尝试编写代码，以便识别随机折线（非闭合）上的随机点位于哪一侧。折线被认为是无限的，第一个和最后一个线段延伸到无穷远。如果它们相交，则应将其视为多边形（我尚未为此情况编写代码）。逻辑如下：
1. 定义折线的顶点，距离待考虑点最近。变量minimum2p是到该顶点的距离，I2p是该顶点的索引。
2. 定义折线的线段，距离待考虑点最近。仅计算与从待考虑点垂直相交的那些线段（变量count_s）。变量minimum2s是到线段的最小距离；I2p是该线段第一个顶点的索引；flag是布尔变量，存储有关相交垂线的信息。
1. 定义折线的顶点，距离待考虑点最近。变量minimum2p是到该顶点的距离，I2p是该顶点的索引。
2. 定义折线的线段，距离待考虑点最近。仅计算与从待考虑点垂直相交的那些线段（变量count_s）。变量minimum2s是到线段的最小距离；I2p是该线段第一个顶点的索引；flag是布尔变量，存储有关相交垂线的信息。
3. 接下来只需要选择适当的片段进行比较，例如使用链接link-1，link-2或link-3中的想法。我尝试了这里的方法，但它在许多特殊情况下都不起作用。对于折线的内部点，我使用最佳答案。因此，我的方法如下：
4. 首先，检查它是折线的第一个还是最后一个顶点。如果是这种情况，则所选的段要么是第一个要么是最后一个，但前提是没有其他比第一个或最后一个更接近的段。如果有另一个段，则我选择那个段。
5. 接下来，如果步骤4不成立，我会检查折线的内部顶点。如果附近也有一个接近的线段，那么我将比较索引I2p和I2s（如果后者存在）。如果它们相同，则在选择要比较的正确线段时没有歧义。如果它们不同，则更偏爱最靠近的线段而不是最靠近的顶点。
6. 最后，如果附近没有线段（从穿过线段的点的垂直意义上），则对于内部顶点，我会应用这里的最佳答案的想法（链接）。
这里是不同折线的结果，它们由其顶点的X和Y坐标定义，分别存储在'polylineX'和'polylineY'中（红色表示“左”位置，灰色表示“右”位置，黑色表示折线上的位置，蓝色线表示折线）。
您可以注意到，对于相对平滑的折线，代码可以正常工作。但是，对于更锐利或某些方面复杂的折线，代码无法正常工作。我在我的代码中漏掉了什么？应该添加什么条件以考虑某些情况？
代码如下：
clear all
close all
clc
clf
polylineX = [0 1 2 3 4 5 6 7 8];
polylineY = [-10 20 -13 18 -17 16 -21 23 -25];
hold on
title(['polylineX=[',num2str(polylineX),'], polylineY=[',num2str(polylineY),']'])
chosen = 0;
span = 60;
for ii = 10:70
for jj = 30:60
ii
jj
position = -2;
point = [(jj-round(span/2))/1 (ii-round(span/2))/1];
axis equal
plot(polylineX,polylineY,'.-','MarkerSize',1,'LineWidth',1);
distance2p = zeros(1,length(polylineX)); % distances from the point to the points (2p) of the polyline
distance2s = zeros(1,length(polylineX)-1); % distances from the point to the segments (2s) of the polyline
flag = zeros(1,length(polylineX)-1);
count_s = 0; % counter of segments, which are intersected by the normal pointing from the 'point'
k = 0;
for i = 1:length(polylineX)-1
pos = sign((polylineX(i+1) - polylineX(i)) * (point(2) - polylineY(i)) -...
(polylineY(i+1) - polylineY(i)) * (point(1) - polylineX(i)));
% computing the distances from the 'point' to all segments and mark if
% the distance vectors intersect the segments
[flag(i),distance2s(i)] = distanceToLine([polylineX(i) polylineX(i+1)],[polylineY(i) polylineY(i+1)],[point(1) point(2)]);
if flag(i)
if k == 0
minimum2s = distance2s(i);
I2s = i;
end;
k = 1;
count_s = count_s + 1; % count segments, which are intersected by the normal pointing from the 'point'
if distance2s(i) < minimum2s
I2s = i;
minimum2s = distance2s(i);
end;
end;
end;
% first compute the distances between the 'point' under consideration and the
% points of the given polyline
for i = 1:length(polylineX)
distance2p(i) = sqrt((point(1)-polylineX(i))^2+(point(2)-polylineY(i))^2);
end;
[minimum2p,I2p] = min(distance2p);
clear k pos i
% now we need to choose which segment of the polyline to compare our 'point' with. These
% segments are either adjacent to that point of the polyline, which is the closest
% to the 'point' of interest, or the closest to the 'point' segment, which
% has an intersection with the normale pointing from the 'point'.
if I2p == 1 % if the 'point' is near the start of polyline
if exist('minimum2s','var')
if I2p == I2s
chosen = I2p;
else
chosen = I2s;
end;
else
chosen = I2p;
end;
elseif I2p == length(polylineX) % if the 'point' is near the end of polyline
if exist('minimum2s','var')
if I2s == I2p-1
chosen = I2p - 1;
else
chosen = I2s;
end;
else
chosen = I2p - 1;
end;
else
if exist('minimum2s','var')
if I2p == I2s
chosen = I2p;
else
chosen = I2s;
end;
else
pos1 = sign((polylineX(I2p) - polylineX(I2p-1)) * (point(2) - polylineY(I2p-1)) -...
(polylineY(I2p) - polylineY(I2p-1)) * (point(1) - polylineX(I2p-1)));
% position of the second segment relative to the first segment
pos2 = sign((polylineX(I2p) - polylineX(I2p-1)) * (polylineY(I2p+1) - polylineY(I2p-1)) -...
(polylineY(I2p) - polylineY(I2p-1)) * (polylineX(I2p+1) - polylineX(I2p-1)));
if (pos1 == 1 && pos2 == 1) || (pos1 == -1 && pos2 == -1)
chosen = I2p;
elseif pos1 == 0 || pos2 == 0
chosen = I2p;
else
chosen = I2p - 1;
end;
end;
end;
position = sign((polylineX(chosen+1) - polylineX(chosen)) * (point(2) - polylineY(chosen)) -...
(polylineY(chosen+1) - polylineY(chosen)) * (point(1) - polylineX(chosen)));
if position == 1
plot(point(1),point(2),'r.','MarkerSize',5)
elseif position == -1;
plot(point(1),point(2),'.','Color',[0.9 0.9 0.9],'MarkerSize',5) % gray color
elseif position == 0
plot(point(1),point(2),'k.','MarkerSize',5)
elseif position == -2
plot(point(1),point(2),'g.','MarkerSize',5)
end;
pause(0.00000001)
clear chosen count_s distance2p distance 2s flag I2p I2s minimum2p minimum2s point pos1 pos2 position
end;
end;
