这确实是归纳法的思想,并且类似于著名的
"L-Tile" covering 示例。
正如您所说,您已经解决了k = 2的问题,解决小例子是解决问题的一个好的和正确的起点,但我认为对于k = 2的情况,这个问题有一些棘手,主要是由于每种类型不能超过40%的限制。
然后对于k> 2,比如在您的示例中k = 3,我们尝试利用您已经解决的问题,即k = 2的情况。
通过非常简单的观察,人们可以注意到对于k = n,它实际上可以由4个k = n-1的情况组成(见下面的图像)
现在中间的阴影部分形成了一个可以用1个B型填充的孔,因此我们可以先填充4个小的n-1情况并用B型填充孔...
但是这种构造面临一个问题:B型将超过40%的面积!
考虑 k = 2 的情况,无论如何填充区域,都必须使用 2 个 B 类型,我没有强有力的证明,但通过一些 brute force 的尝试和错误,你应该会被说服。然后对于 k = 3,我们有 4 个小三角形,意味着我们有 2 * 4 = 8 个 B 类型,再加上 1 个来填补空洞,就会得到 9 个 B 类型,每个使用 1.5 平方单位,总共使用了 13.5 平方单位。
当 k = 3 时,总面积为 (2^3)^2 / 2 = 32 平方单位
13.5/32 = 0.42.... 违反了限制!
那怎么办呢?这就是为什么我们必须使用一个技巧来处理 k = 2 情况的原因(我假设你已经阅读过这部分,因为你说你知道如何处理 k = 2 情况)。
首先,我们知道使用我们的构造方法从4个小三角形组成一个大三角形时,“只有B型”会违反这个约束条件(即40%的面积),您可以自行验证。因此,我们想要减少使用B型的总数,但是每个小三角形必须至少使用2个B型,所以我们唯一可以减少的地方是大三角形中间的空洞,我们可以使用其他类型的三角形来代替B型吗?同时,我们希望小三角形的其他部分保持不变,这样我们就可以使用相同的论证方法进行归纳(即通常情况下,使用相同的构造方法从4个$2^{n-1}$三角形形成$2^n$个三角形)。
如果我们特别设计k=2的情况,答案是肯定的。请看下面我的构造方式:(可能还有其他的构造方式,但我只需要知道一个)
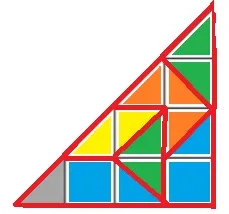
“诀窍是我有意将一个B型方块移到了空的(灰色)三角形旁边。现在我们停一下,进行一些验证:
为了构建k = 2的情况,我们使用:
- 2个A型=2平方单位<40%
- 2个B型=3平方单位<40%
- 1个C型=1.5平方单位<40%
- 1个D型=1平方单位<40%
总共使用7.5平方单位,很好。
现在想象我们使用完全相同的方法来构造那4个三角形以制作一个大三角形,中间仍然是一个形状为B型的空洞,但现在我们不再用1个B型填充它,而是用A型和D型
同时与旁边的3个B型一起(回顾k = 2的情况),填补空洞(我使用与上面相同的颜色方案以便易于理解),我们对构成中心空洞的所有3个小三角形都这样做。”
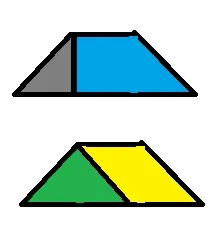
这是最后一部分(我知道它很长...)我们减少了构建大三角形所需的B型数量,但同时增加了使用A型和D型的数量!那么这种新的构建方法有效吗?
首先注意到,除了紧邻灰色三角形的B型之外,它不会改变小三角形的任何部分,即如果满足40%的约束条件,则此方法是归纳和递归填充2 ^ n边长三角形的。
然后让我们再次计算使用每种类型的数量。
对于k = 3,总单位数为32,我们使用:
- 2 * 4 + 3 = 11个A型= 11平方单位<40%
- 2 * 4-3 = 5个B型= 7.5平方单位<40%
- 1 * 4 = 4个C型= 6平方单位<40%
- 1 * 4 + 3 = 7个D型= 7平方单位<40%
总共覆盖了31.5个单位,很好,现在让我们证明对于k = n> 3,满足40%的约束条件。
令FA(n-1)为使用我们的新方法填充2^n-1个三角形所需的A类面积总和,同样地,FB(n-1)、FC(n-1)、FD(n-1)也有类似的定义。
假设F*(n-1)成立,即不超过总面积的40%,我们证明F*(n)成立。
我们得到:
FA(n) = FA(n-1)*4 + 3*1
FB(n) = FB(n-1)*4 - 3*1.5
FC(n) = FC(n-1)*4
FD(n) = FD(n-1)*4 + 3*1
我们只展示FD(n)的证明,其他三个用相似的方法(M.I.)证明。
使用代换法,FD(n) = 2*(4^(n-2)) - 1 for n>=3 (你至少应该尝试自己提出这个方程式)
我们想要证明 FD(n)/(2^2(n)/2) < 0.4
即:
2FD(n)/4^n < 0.4
考虑左式,
左式 = (4*(4^(n-2)) - 1)/4^n
< 4^(n-1)/4^n = 1/4 < 0.4 证毕
这意味着使用这种方法,对于任何2^k边的三角形(k >= 3),所有A-D类型都不会超过总面积的40%,最后我们归纳地展示了一种满足所有约束条件的构建此类三角形的方法。
简而言之:
- 难点在于满足40%的面积限制
- 先在k=2的情况下使用特殊构造,尝试用它来建立k=3的情况(然后是k=4、k=5...归纳法的思想!)
- 当使用k=n-1的情况来建立k=n的情况时,写下每种类型所消耗的总面积公式,并证明它们不会超过总面积的40%
- 结合第2和第3点,这是一种归纳方法,用于证明对于任何k>=2,都有一种方法(我们描述的方法)可以填充2^k边的三角形,而不违反任何限制

