如何在三维空间中将一个点投影到平面上？

Question

我有一个三维点（point_x，point_y，point_z），我想将它投影到三维空间中定义的由一个点坐标（orig_x，orig_y，orig_z）和一个垂直向量（normal_dx，normal_dy，normal_dz）定义的二维平面上。

应该如何处理？

- George

---

请参考以下链接中的“正交投影”部分：http://en.wikipedia.org/wiki/3D_projection - Edward Loper

从下面的答案中看来，似乎有关于这个投影你正在寻找什么结果的混淆：它是平面上最接近你感兴趣点的3D点吗？还是平面坐标系中的2D点？还是其他什么？ - tmpearce

我认为他想要找到平面上距离点(point_x, point_y, point_z)最近的点，也就是图表中标记为(planar_x, planar_y, planar_z)的点。(所有坐标都在全局坐标系中。) 因此，我相信@tmpearce的答案是正确的。 - aldo

Answer 1

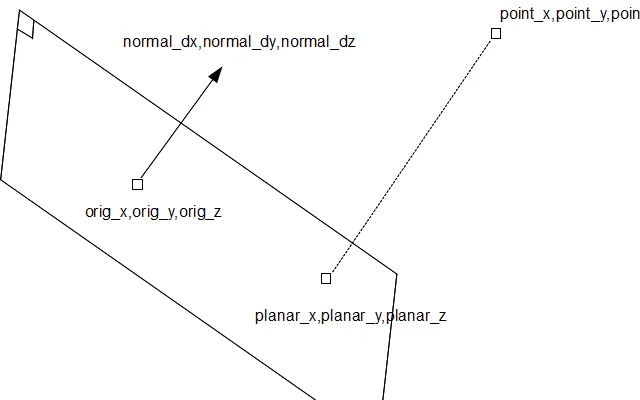
1. 将orig点到兴趣点的距离作为向量:

v = point-orig (在每个维度上);

2. 将该向量与单位法线向量n进行点乘:

dist = vx*nx + vy*ny + vz*nz; dist = 沿法线从点到平面的标量距离

3. 将单位法向量乘以距离，并从您的点中减去该向量。

projected_point = point - dist*normal;

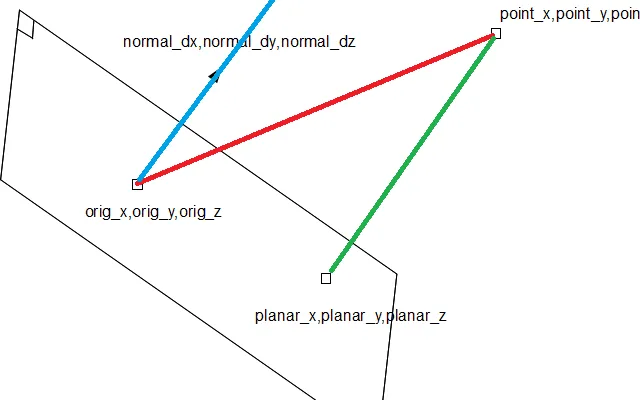
图示：我稍微修改了您的图片。红色是v。 dist是蓝色和绿色的长度，等于v点积normal。 蓝色是normal*dist。 绿色是与蓝色相同的向量，它们只是在不同的位置绘制。 要找到planar_xyz，请从point开始，并减去绿色向量。

- tmpearce

---

需要的是叉积，而不是点积。但这还不够。请阅读我的答案。 - valdo

取决于你是想要到平面的最近距离还是垂直点。我理解他的帖子是想要最近的点。 - tmpearce

好的，如果是这样 - 你是对的。但我理解它的方式不同。单词“投影”通常意味着在平面上获取2个坐标。尽管如此，让问题的作者决定他/她的意思。 - valdo

你需要加入 d 来获取点到平面的垂直距离，否则你会假设该平面通过原点。 - bobobobo

@dev_nut 是的，问题中的“normal”向量已经被定义为单位长度，并且我继续以这种方式使用它。感谢您的评论 - 它让我意识到这值得在答案中澄清。我编辑了答案，以明确表明单位法线是适当的向量。 - tmpearce

Answer 2

这很简单，你只需要找到从点P到平面的垂线距离（缩写为|_），然后在平面法向量方向上以垂线距离反向平移P。结果是平移后的P位于平面上。

以一个容易的例子（我们可以通过检查来验证）：

设 n=(0,1,0)，P=(10,20,-5)。

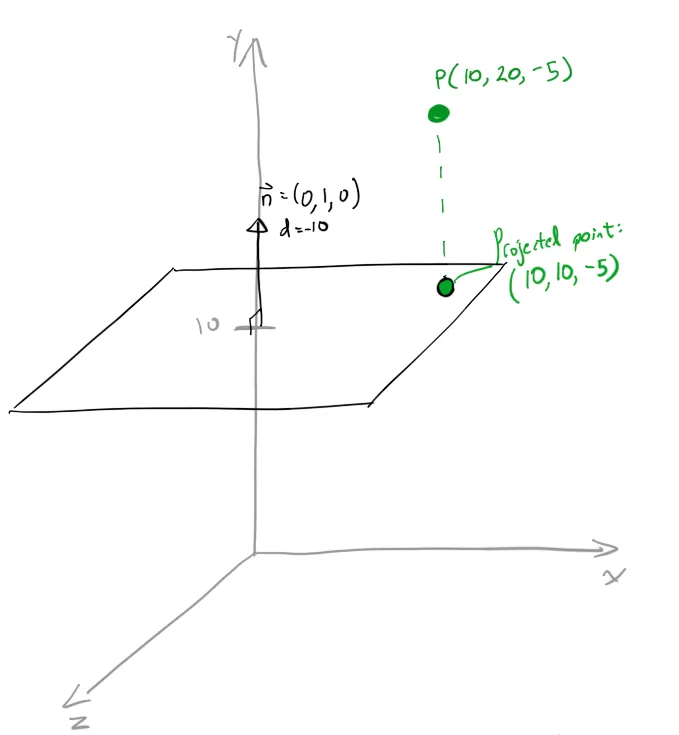
投影点应该是(10,10,-5)。 你可以通过检查发现Pproj在平面上垂直距离为10单位，如果它在平面上，它将有y=10。

那么我们如何分析性地找到它呢？

平面方程是Ax+By+Cz+d=0。这个方程的意思是"为了使一个点(x,y,z)在平面上，它必须满足Ax+By+Cz+d=0"。

上面绘制的平面的Ax+By+Cz+d=0是什么方程？

平面的法向量是n=(0,1,0)。d可以通过使用已经在平面内的测试点来简单地找到：

(0)x + (1)y + (0)z + d = 0

点 (0,10,0) 在该平面上。将其代入，我们得到 d=-10。因此，该平面的方程为 0x + 1y + 0z - 10 = 0（如果简化，可以得到 y=10）。

d 的一个不错的解释是它表示“你需要沿法线方向平移该平面多远才能使其经过原点的垂直距离”。

无论如何，一旦有了 d，我们就可以通过以下公式找到任意点到该平面的 |_ 距离：

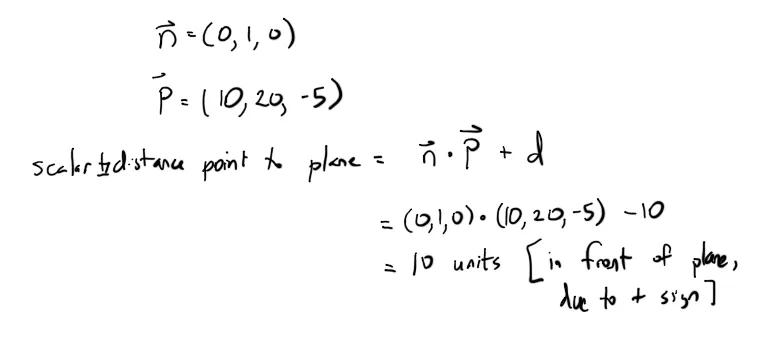
到平面的 |_ 距离有三个可能的结果类别：

• 0：恰好在平面上（由于浮点精度问题几乎不会发生）
• +1：> 0：在平面前面（法线方向一侧）
• -1：< 0：在平面后面（法线方向相反一侧）

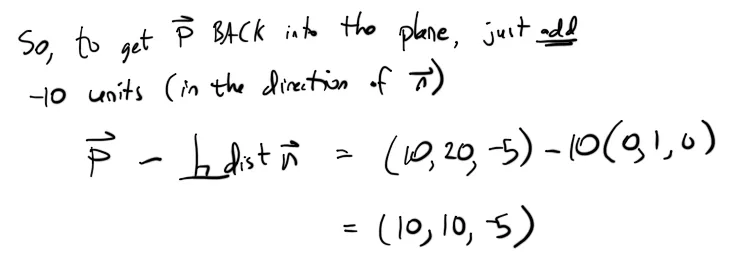
你可以通过上图检验其正确性。

- bobobobo

---

@bobobobo：你通过写“…just add -10…”让我感到困惑了。 你隐晦地将__n__ ⋅ p + _d_的结果乘以-1，只是为了用“add”而不是“subtract”。:P我花了一些时间解释你的答案，所以我来总结一下。给定由法线__n__和标量_d_定义的平面，并给出一个点__p__，可以通过以下方式找到在该平面上距离给定点__p__最近的点__p__'：

1. p' = p - (n ⋅ p + d) * n

如果平面是由法线__n__和平面上的一点__o__定义的，则您建议使用：

2. d = -n ⋅ o

- Mr.H

Answer 3

以法向量n和点o定义平面的方法

这种方法在@tmpearce的答案中已经解释过了。

给定一个以法向量n和位于平面上的点o的点法式定义的平面，可以通过以下方式找到距离给定点p最近的点p'：

1. p' = p - (n ⋅ (p - o)) × n

以法向量n和标量d定义平面的方法

这种方法在@bobobobo的答案中已经解释过了。

给定一个由法向量n和标量d定义的平面，可以通过以下方式找到距离给定点p最近的点p'：

2. p' = p - (n ⋅ p + d) × n

如果您有一个点法式定义的平面（即平面由法向量n和位于平面上的点o定义），@bobobobo建议找到标量d：

3. d = -n ⋅ o

并将其插入方程2中。 这会得到：

4. using n and d: 1 multiplication + 1 addition
2. d can be pre-calculated once for a given plane, and then reused multiple times. This can save significant computation time in certain applications.

Therefore, equation 5 is equivalent to equations 1 and 4, but may provide a more efficient implementation in some cases.

差异说明

仔细观察方程式1和4。通过比较它们，您会发现方程式1使用n ⋅ (p - o)，而方程式4使用n ⋅ p - n ⋅ o。实际上这是写同一件事的两种方式：

5. n ⋅ (p - o) = n ⋅ p - n ⋅ o = n ⋅ p + d

因此，我们可以把标量d解释为“预计算”。如果一个平面的n和o已知，但是只用来计算n ⋅ (p - o)，我们可以选择使用n和d来定义平面，并计算n ⋅ p + d，因为我们刚刚证明它们是相同的。

此外，对于编程，使用d有两个优点：

1. 现在查找p'的计算更简单，特别是对于计算机。比较:
• 使用n和o: 3次减法+3次乘法+2次加法
• 使用n和d: 1次乘法+1次加法
2. d可以针对给定平面进行预计算，然后多次重复使用。这可以在某些应用程序中节省大量计算时间。

因此，方程式5等同于方程式1和4，但在某些情况下可能提供更有效的实现方式。

5. 使用n和d: 0减法 + 3乘法 + 3加法。
2. 使用d将平面的定义限制为仅有4个实数(3个用于n，加上1个d), 而不是6个(3个用于n，加上3个用于o)。这可以节省⅓的内存。

- Mr.H

---

这将非常有帮助，只是我不确定 . 和 * 有什么区别。您能简单地展示每个向量组件的操作归结为什么吗？ - M2tM

嗨@M2tM。我写这篇答案已经有一段时间了。⋅表示点积。表示叉积。（后者对我自己来说也不是很明显，但可以从__p__和__p'在同一个平面上且__n__为法向量这一事实中推断出来。这意味着__p'=p+某个_正交_于__n__的向量。正交向量是指向叉积方向的提示。）我用×替换了答案中的任何，以便未来读者。谢谢你的注意！ - Mr.H

太棒了，谢谢！很好的想法，我猜“.”是点积，但我得到的结果与预期不符，所以我想深入挖掘一下并询问一下，结果确实如此，我把“*”当作乘法而不是叉积。感谢您重新访问这个问题！ - M2tM

@Mr.H，我们如何在标量和向量之间进行叉积？如果我没记错的话，叉积是在两个向量之间定义的吧？（https://en.wikipedia.org/wiki/Cross_product）方程2和4包含（**n⋅p** + d）和（n⋅p - n⋅o），它们都是标量。我有误解吗？ - Glxblt76

至少有一个方程是错误的（第一个方程）。那不应该是一个叉乘。 - undefined

Answer 4

仅提供平面原点和法向量是不足够的。这定义了三维平面，但并未定义平面上的坐标系。

想象一下，您可以围绕法向量旋转平面，以其原点为中心（即将法向量置于原点并“旋转”）。

然而，您可以找到投影点到原点的距离（这显然不随旋转而变化）。

从三维点中减去原点。然后与法线方向进行叉乘。如果您的法向量已被标准化，则结果向量的长度等于所需值。

编辑

完整的答案需要一个额外的参数。例如，您还提供表示平面x轴的向量。
因此，我们有向量n和x。假设它们被标准化。

原点由O表示，您的三维点为p。

那么，您的点将进行以下投影：

x = (p - O)·x

y = (p - O)·(n × x)

- valdo

---

你是正确的，该点在平面上方，并垂直于平面。因此，您说要执行“点-原点”，然后用法线向量与前一个向量进行叉乘，结果就是我想要的？ - George

仅为了澄清未来的读者：如果你有 y 而不是 n，则 n 乘以 x 的结果为 y。在二维上的投影只是在规范化轴方向上进行点积投影。 - Tim Kuipers

Answer 5

让 V = (orig_x, orig_y, orig_z) - (point_x, point_y, point_z)

N = (normal_dx, normal_dy, normal_dz)

令 d = V·N;

投影点 P = V + d·N

- PermanentGuest

---

不太对：一切都很好，直到最后一步，但是你想要点 - d*N。 - tmpearce

我的第一步是：V = (orig_x, orig_y, orig_z) - (point_x, point_y, point_z)。因此，我的基准点是“point”，而不是原点.. 所以，我应该添加.. - PermanentGuest

d.N 是点积还是叉积？ - BenKoshy

Answer 6

我认为你应该稍微改变描述平面的方式。事实上，描述平面的最佳方式是通过一个向量n和一个标量c

(x, n) = c

常数c（绝对值）是平面到原点的距离，并且等于(P, n)，其中P是平面上的任意一点。

所以，让P成为您的orig点，A'成为新点A在平面上的投影。您需要做的是找到a，使得A' = A - a*n满足平面方程，即

(A - a*n, n) = (P, n)

解出a，您会发现

a = (A, n) - (P, n) = (A, n) - c

这给出了

A' = A - [(A, n) - c]n

使用您的名称，这样阅读

c = orig_x*normal_dx + orig_y*normal_dy+orig_z*normal_dz;
a = point_x*normal_dx + point_y*normal_dy + point_z*normal_dz - c;
planar_x = point_x - a*normal_dx;
planar_y = point_y - a*normal_dy;
planar_z = point_z - a*normal_dz;

注意：如果您存储了c =（P，n）而不是orig点P，则代码将节省一个标量积，这基本上意味着对于每个投影减少25％的Flops（在该例程在代码中使用多次的情况下）。

- bartgol

Answer 7

设r为需要投影的点，p为投影结果。设c为平面上的任意一点，n为平面法向量（不一定已标准化）。写出p=r+ m d，其中m为标量，如果没有解，则将其视为不定。 由于（p-c）·n=0，因为平面上所有点都满足这个限制，因此有(r-c)·n+m(d.n)=0，因此m=[(c-r)·n]/[d.n]，其中点乘（.）被使用。但是，如果d.n=0，则没有解。例如，如果d和n相互垂直，则无解。

- Peter