贝尔-福特算法是否可以在边的任意顺序下运行？

Question

我刚开始学习新算法，但在阅读geeks for geeks上的贝尔曼-福特算法时遇到了困难：- http://www.geeksforgeeks.org/dynamic-programming-set-23-bellman-ford-algorithm/ 其中写道-

该算法以自下而上的方式计算最短路径。它首先计算最多具有一条边的路径的最短距离。然后，它计算最多具有2条边的最短路径，依此类推。

在外部循环的第i次迭代之后，将计算最多具有i条边的最短路径。在任何简单路径中，最多可以有|V|-1条边，这就是为什么外部循环运行|v|-1次的原因。假设没有负权重环，那么我们的想法是，如果我们已经计算出至多具有i条边的最短路径，则对所有边进行迭代保证给出最多(i+1)条边的最短路径。

让我们通过以下示例图形来理解算法。 这些图像来自此来源。

假设给定的源顶点是0。将所有距离初始化为无穷大，除了与源本身的距离。图中总共有5个顶点，因此所有边必须处理4次。

如果边的顺序是（AB），（BE），（ED），（DC），（AC），（BC），（DB），（BD）等，则仅在一次迭代中，它将计算具有甚至2-3条边的最短路径，这与“首先计算最多具有一条边的最短路径。然后，它计算最多具有2条边的最短路径，以此类推。在外部循环的第i次迭代之后，计算了最多具有i条边的最短路径”这一说法相矛盾。因此，通过改变边的顺序，这个语句将被证明是错误的。

让我们通过以下示例图形来理解算法。这些图像来自此来源。

假设给定的源顶点是0。将所有距离初始化为无穷大，除了与源本身的距离。图中总共有5个顶点，因此所有边必须处理4次。

让我们按照以下顺序处理所有边缘：(B,E)，(D,B)，(B,D)，(A,B)，(A,C)，(D,C)，(B,C)，(E,D)。当第一次处理所有边缘时，我们得到以下距离。第一行显示初始距离。第二行显示处理(B,E)，(D,B)，(B,D)和(A,B)后的距离。第三行显示处理(A,C)后的距离。第四行显示处理(D,C)，(B,C)和(E,D)后的距离。 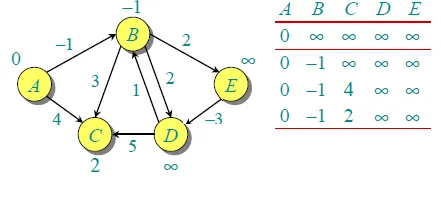第一次迭代保证给出最多为1个边长的所有最短路径。当第二次处理所有边缘时，我们得到以下距离（最后一行显示最终值）。

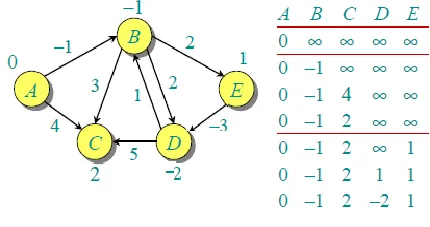
第二次迭代保证给出所有最短路径，这些路径最多只有2条边。算法会再处理所有边2次。在第二次迭代后距离被最小化，因此第三次和第四次迭代不会更新距离。

- coderAJ

---

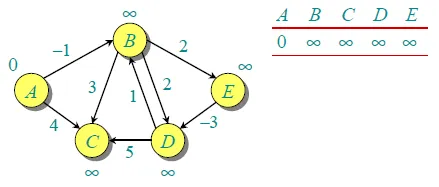
虽然问题的陈述非常清晰和详细，但实际问题有些难以理解。此外，在上面的第一个黄色块中，我认为缺少了边缘 BD 和 DB。 - Codor

是的，你具体在哪里卡住了呢？ :) - Filip Haglund

谢谢，我错过了BD和DB，现在我已经纠正了。我的问题是，我观看了几个贝尔曼-福德算法的视频，并在各种网站上学习了相关知识，得出结论我们可以以任意随机顺序取边，但这里说，在第一次迭代中，它将给出最多1条边的最短路径，依此类推。只有在边的某种特定顺序下才能实现这一点，这似乎是正确的。 - coderAJ

Answer 1

是的，贝尔曼-福特算法可以在任何顺序下处理边缘。事实上，这就是为什么你必须进行 n-1 次迭代的原因。如果你知道边的最佳顺序 - 只需要一次迭代就足够了。

考虑以下图形（所有边缘的权重都是 1）：

 (1) --> (2) --> (3) --> (4) 

如果按顺序处理边缘1->2，2->3，3->4，你将在一次迭代中找到从1到4的最短路径。对于按顺序排列的边缘3->4，2->3，1->2，您需要执行所有3次迭代。

然而，在没有负循环的情况下，无论以何种顺序处理边缘（如果有），n-1次迭代都是最坏情况。

- ead

Answer 2

没错。松弛的顺序无关紧要。

例如，

这里有3个节点，因此可以进行两次松弛。如果反向开始从节点b到节点a进行松弛，则第一次迭代会产生b:infinity、a:2。然后第二次迭代是b:5、a:2。在第一次迭代中，不能更新b，因为只使用了一条边，只能更新距离一个边之外的a节点。第二次迭代是源到任何地方使用了两条边，因此最终可以更新b。在第一次迭代中，b无法更新，因为a还没有准备好。

那么我们来看一下正向更新怎么样？在第一次迭代中，它将是a:2和b:5。第二次迭代仍然是a:2和b:5。沿着前进，让所有连续的节点都准备好更新距离，所以更多的迭代不会改变值。但是，有人可能会想，如果我对101个节点进行100次迭代，并且我正在进行正向更新，是否有可能在第一次迭代中就更新了所有内容，在99次迭代中没有更改，而在第100次迭代时有一个节点距离减少？ 不，这是不可能的，因为除非存在负环，否则正向更新在第1次迭代后不会引起更改。

您可以在此处阅读有关Bellman-Ford的更多信息：https://medium.com/@logicdevildotcom/dynamic-programming-applied-to-graphs-f33b6b8a8247

- Suhyun Kim

Answer 3

您所提到的带有注释的表格行

第四行显示了处理 (D,C), (B,C) 和 (E,D) 时的情况。

是不正确的。这将意味着存在一条从 A 到 C 的长度为2的路径，该路径由最多一个边组成 - 然而，这样的路径不存在。

- Codor

Answer 4

示例图表

在这个有向加权图中，假设我们按照以下顺序放松边缘： (u,v)，(s,u) 和 (s,v)。这里源是 “s”。因此，在 Bellman Ford 算法的初始化步骤中，我们有 d(s)=0，d(u)=d(v)=∞。由于我们总共有 3 个顶点，所以算法应该进行 3-1=2 次迭代，才能为从源到顶点产生最短距离。在每次迭代的每个步骤中，我们需要对每个边缘 (u,v) 进行松弛步骤，检查是否满足 d(u) + w(u,v) < d(v)，如果满足这个条件，则将 d(v) 设置为 d(u) + w(u,v)。

第一次迭代后: d(u)=3，d(v)=7 第二次迭代后: d(u)=3，d(v)=5

因此，正如您所看到的，第一次迭代不能保证给出所有最多为1个边长的最短路径。因为在这个例子中，我们只有在第二次迭代后才能得到节点“v”的1个边长的最短距离。然而，如果我们在图中强制使用三角不等式，则该语句将成立。

现在回到您最初的问题，是的，Bellman-Ford算法可以以任意顺序放松边缘，就像@ead上面很好地回答的那样。但在最终迭代步骤结束时，该算法将为您提供每个节点从源节点的最短距离。

- Saurav Kumar Sahu