Python中强度函数的积分

Question

Python中强度函数的积分

pythonscipyintegralnumerical-integration

4

有一个函数可以确定圆形孔径的弗朗霍夫衍射图案的强度...(更多信息)

在距离x=[-3.8317, 3.8317]的积分必须约为83.8%（如果假设I0为100），而当您将距离增加到[-13.33，13.33]时，它应该约为95％。但是当我在Python中使用积分时，答案是错误的...我不知道我的代码哪里出错了:(

from scipy.integrate import quad
from scipy import special as sp
I0=100.0
dist=3.8317
I= quad(lambda x:( I0*((2*sp.j1(x)/x)**2))  , -dist, dist)[0]
print I

积分的结果不能超过100（I0），因为这是I0的衍射...我不知道...可能是缩放...也可能是方法！:(

- Saeed

3个回答

3

请注意，您还可以使用Sympy获得集成的闭式解：

import sympy as sy

sy.init_printing()  # LaTeX like pretty printing in IPython

x,d = sy.symbols("x,d", real=True)

I0=100
dist=3.8317
f = I0*((2*sy.besselj(1,x)/x)**2)  # the integrand
F = f.integrate((x, -d, d))  # symbolic integration
print(F.evalf(subs={d:dist}))  # numeric evalution

F的求值结果为：

1600*d*besselj(0, Abs(d))**2/3 + 1600*d*besselj(1, Abs(d))**2/3 - 800*besselj(1, Abs(d))**2/(3*d)

使用besselj(0,r)对应于sp.j0(r)。

- Dietrich

1

当在 x = 0 处计算雅可比矩阵时，它们可能是积分算法中的奇点。您可以使用 "points" 排除这些点以进行积分。

f = lambda x:( I0*((2*sp.j1(x)/x)**2))
I = quad(f, -dist, dist, points = [0])

我得到以下结果（这是你想要的结果吗？）

331.4990321315221

- varantir

网页内容由stack overflow 提供, 点击上面的

可以查看英文原文，
原文链接

- DrV · Accepted Answer

问题似乎出现在函数在零点附近的行为。如果将函数绘制出来，它看起来非常平滑:

但是，`scipy.integrate.quad` 抱怨舍入误差，这与这个美丽的曲线非常奇怪。然而，该函数在0处未被定义（当然，你正在除以0！），因此积分并不顺利。

您可以使用更简单的积分方法或对函数进行某些处理。您还可以从两侧非常靠近零积分它。但是，通过这些数字查看结果时，积分看起来并不正确。

不过，我认为我知道你的问题所在。就我所记得的而言，你展示的积分实际上是弗朗霍夫衍射的强度（功率/面积）关于距离中心的函数。如果要在某个半径内积分总功率，则必须在二维空间中进行积分。

根据简单的面积积分规则，您应将函数乘以2πr再进行积分（或在您的情况下用x替代r）。然后它变成了：

f = lambda(r): r*(sp.j1(r)/r)**2

或者

f = lambda(r): sp.j1(r)**2/r

或者更好的是：

f = lambda(r): r * (sp.j0(r) + sp.jn(2,r))

最后一种形式最好，因为它不会出现任何奇点。这是基于Jaime在原回答下的评论（请参见本答案下面的评论）。

（请注意，我省略了一些常数。）现在您可以将其从零积到无穷大（没有负半径）：

fullpower = quad(f, 1e-9, np.inf)[0]

然后您可以从其他半径进行积分，并通过全强度对其进行归一化：

pwr = quad(f, 1e-9, 3.8317)[0] / fullpower

如果您尝试更大的半径（13.33），您将得到0.839（非常接近84%）。

pwr = quad(f, 1e-9, 13.33)

这会给出0.954。

需要注意的是，我们通过从1e-9开始积分而不是从0开始引入了一些误差。可以通过尝试不同的起点值来估计误差的大小。在1e-9和1e-12之间，积分结果变化很小，所以它们似乎是安全的。当然，你可以使用比如1e-30，但那样可能会在除法中产生数值不稳定性。（在这种情况下没有，但通常奇点在数值上是有害的。）

还有一件事要做：

import matplotlib.pyplot as plt
import numpy as np

x = linspace(0.01, 20, 1000)
intg = np.array([ quad(f, 1e-9, xx)[0] for xx in x])

plt.plot(x, intg/fullpower)
plt.grid('on')
plt.show()

以下是我们得到的结果：

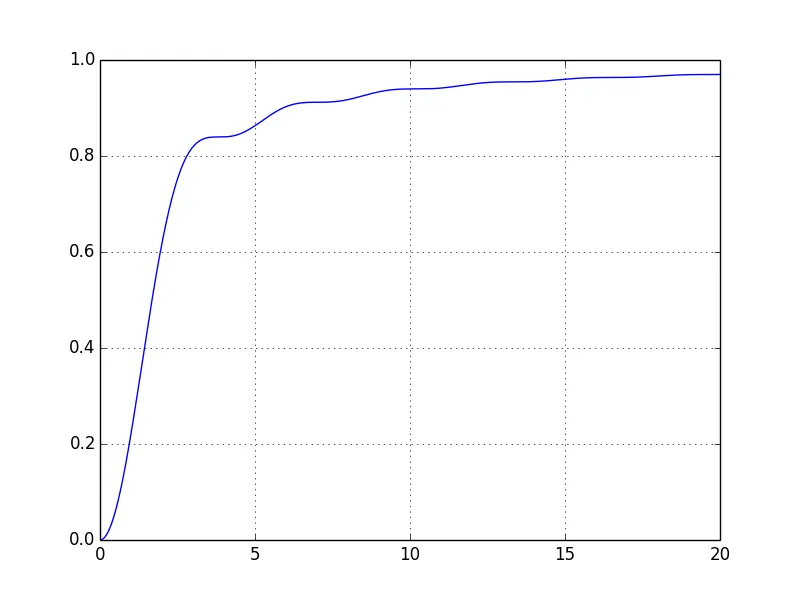
enter image description here

至少这看起来是对的，艾里圆盘的暗色条纹清晰可见。

关于问题的最后一部分：I0定义了最大强度（单位可以是W/m2），而积分给出了总功率（如果强度以W/m2为单位，则总功率以W为单位）。将最大强度设置为100不能保证总功率。这就是为什么计算总功率很重要。

实际上存在一个封闭形式的方程，用于计算辐射在圆形区域上的总功率：

P(x) = P0 ( 1 - J0(x)^2 - J1(x)^2 ),

其中P0是总功率。